一类垂直于正交异性双材料界面的Ⅱ裂纹尖端应力场的理论研究

胡帅帅 李俊林

（太原科技大学 应用科学学院，太原 030024）

文献［1－3]研究了各向同性复合材料中所含垂直裂纹尖端的一系列问题.文献［1]中采用mellin变换法研究垂直裂纹问题，得出裂纹接触界面后，应力的性态指数与材料常数及裂纹集合形状有关.文献［2]中用liyong mellin变换方法，将垂直裂纹问题归结为求解Cauchy型奇异积分方程组，得到半无限长裂纹受集中力作用时，接触点奇性应力场，并对其分布函数进行了数值求解.文献［3]介绍了裂纹垂直于一个非理想双材料界面的情形.

本文利用傅里叶积分变换巧妙地构造出了裂纹尖端的位移场，通过适当的边界连续条件将边值问题转换成带有Cauchy核的奇异积分方程，并给出了应力强度因子的表达式，当两种材料相同时得出与文献［4]一致的结论.

1 力学模型

如图1所示，a≤x≤b，y＝0为垂直界面裂纹，其中心距双材料界面距离为c，x＝0为材料粘结面.x＞0部分是第1种正交异性材料，其材料工程常数为E11、E12、v11、v12和μ1，而x＜0部分是第2种正交异性材料，其材料工程常数为E21、E22、v21、v22和μ2.由于靠近裂纹尖端奇异场的影响，在裂纹表面施加一个纯剪切载荷，也就是

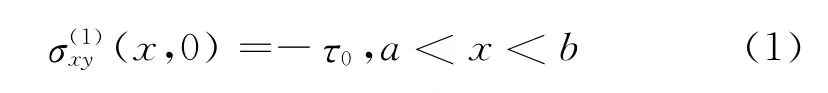
图1 含有垂于正交各向异性双材料界面的II型裂纹

2 基本方程

由弹性力学可知在不考虑体力的情况下，控制方程为

物理方程为

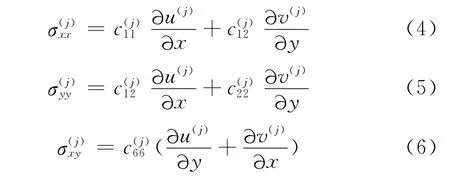
这里j＝1，2分别对应于正交异性材料1与材料2.u（j）和v（j）分别代表x和y方向的位移，也就是u（j）＝u（j）（x，y），v（j）＝v（j）（x，y），c（j）ik为无量纲参数.

控制方程要在如下边界连续条件下求解：

2.1 求解

由于问题的对称性，只需考虑y≥0的情况就可以了，如文献［5－6]中的讨论，通过傅里叶积分变换构造方程（2）～（3）的解为

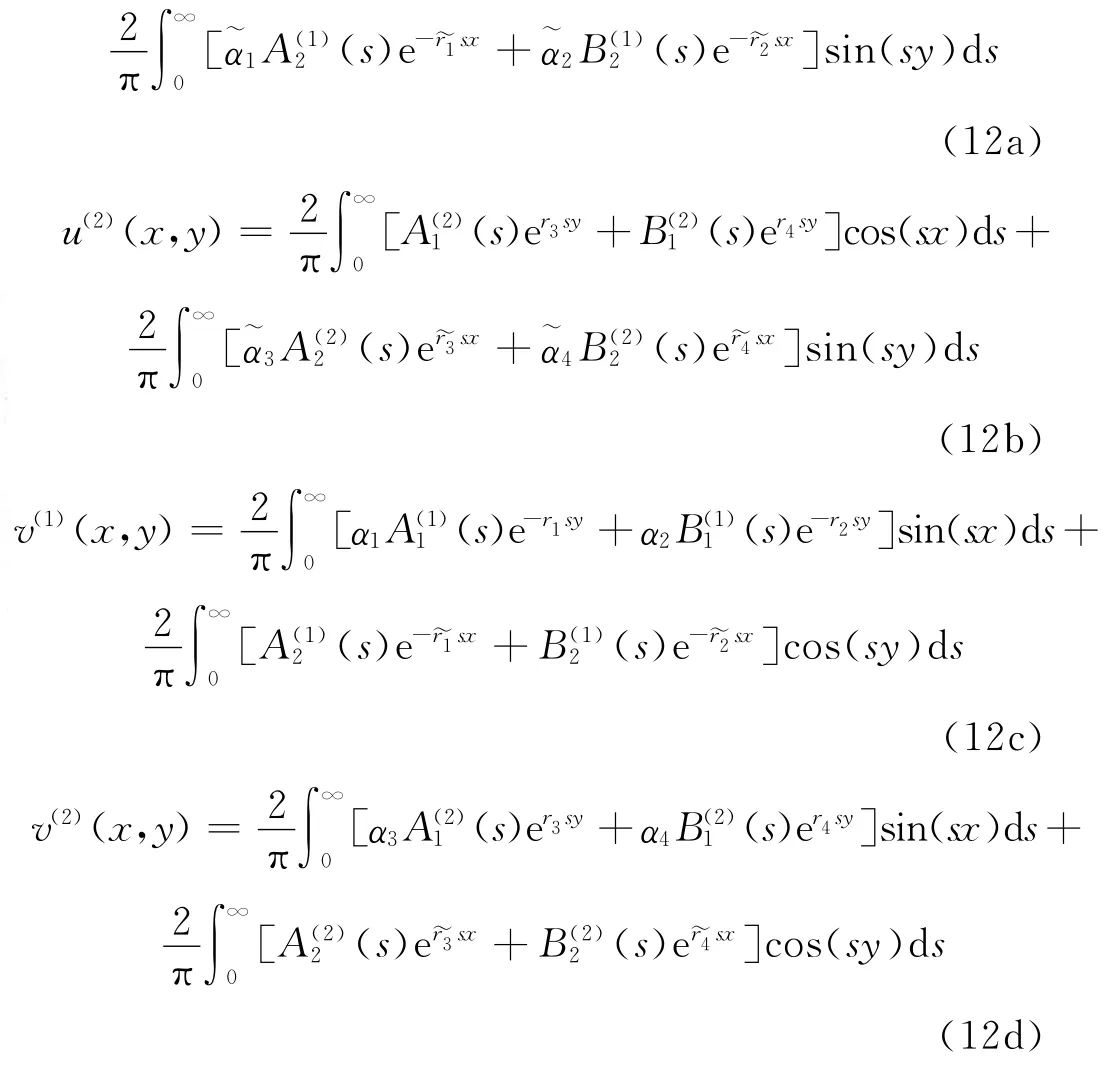
其中

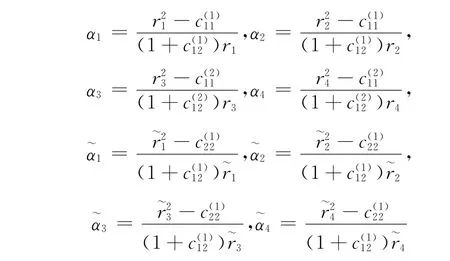
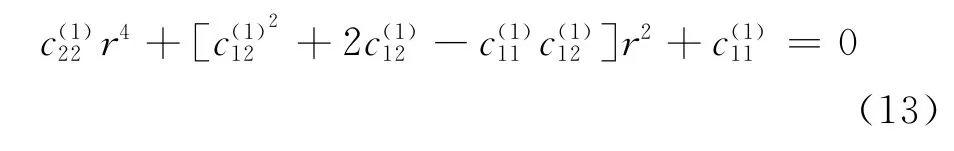
r2j（j＝3，4）是如下方程的正实根

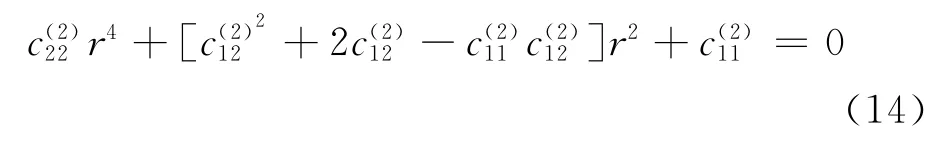
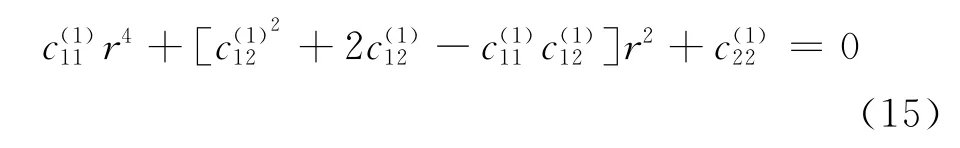
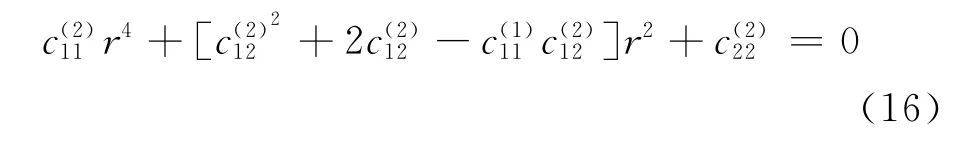
把方程（12a）～（12d）带入物理方程（4）～（6）中可得

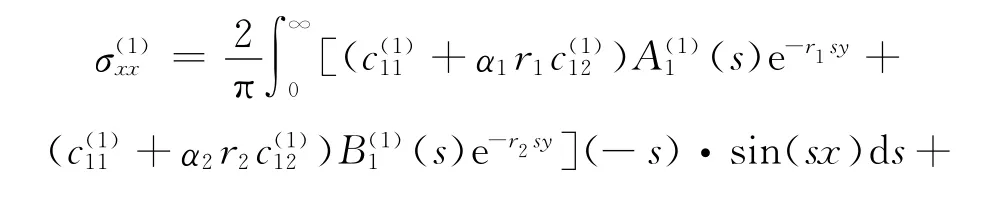
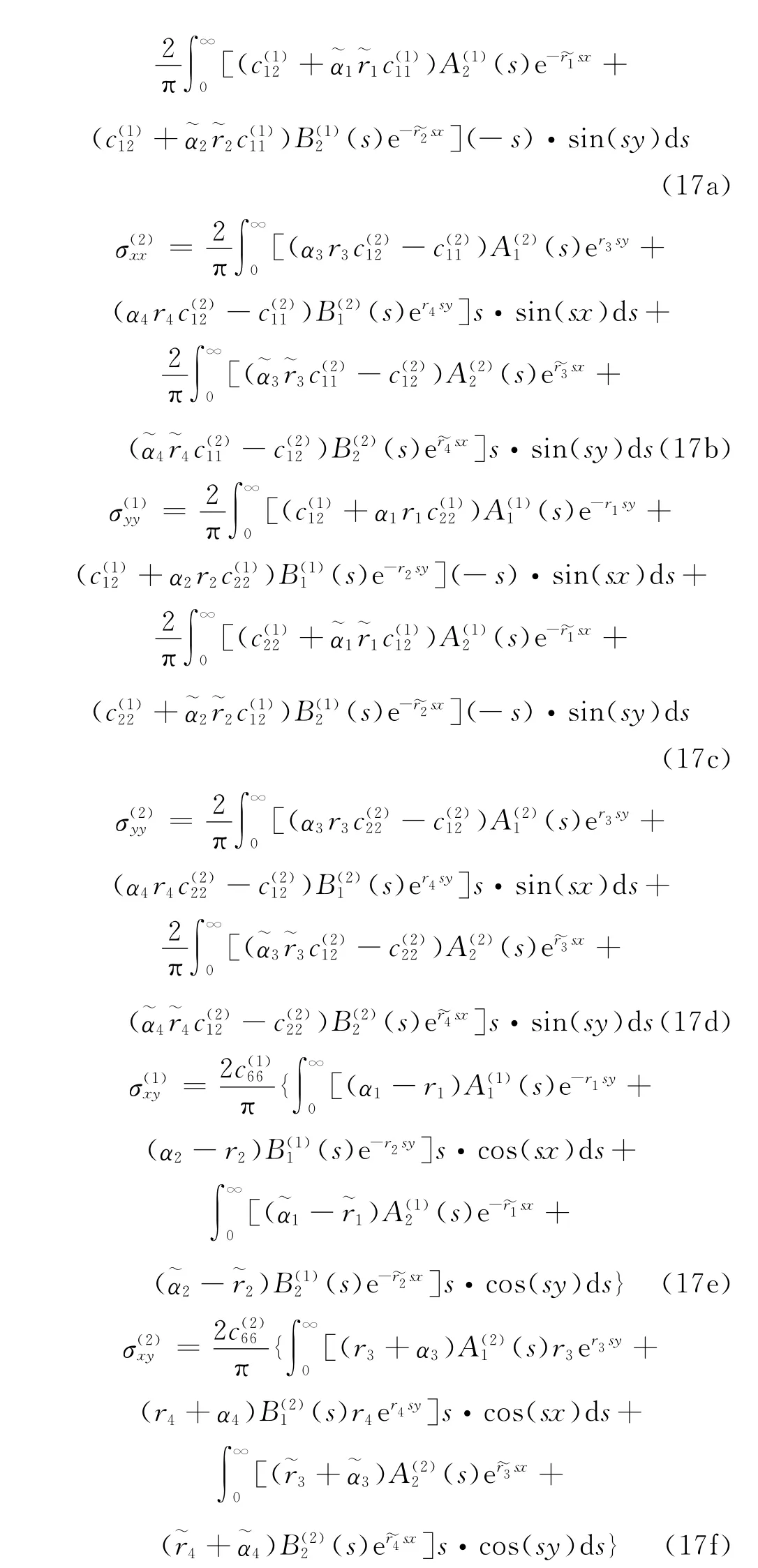
上面的表达式显然满足式（2）～式（6），下面通过适当的连续边界条件得到裂纹尖端的弹性场.找出未知函数由边界连续条件式（7）～式（11）可以得到

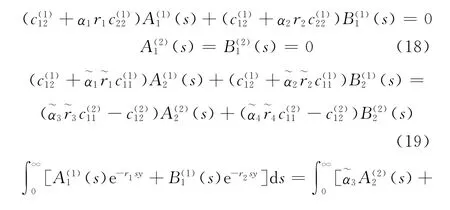
（s）＝0，对式（20）、式（22）化简可以得到

其中

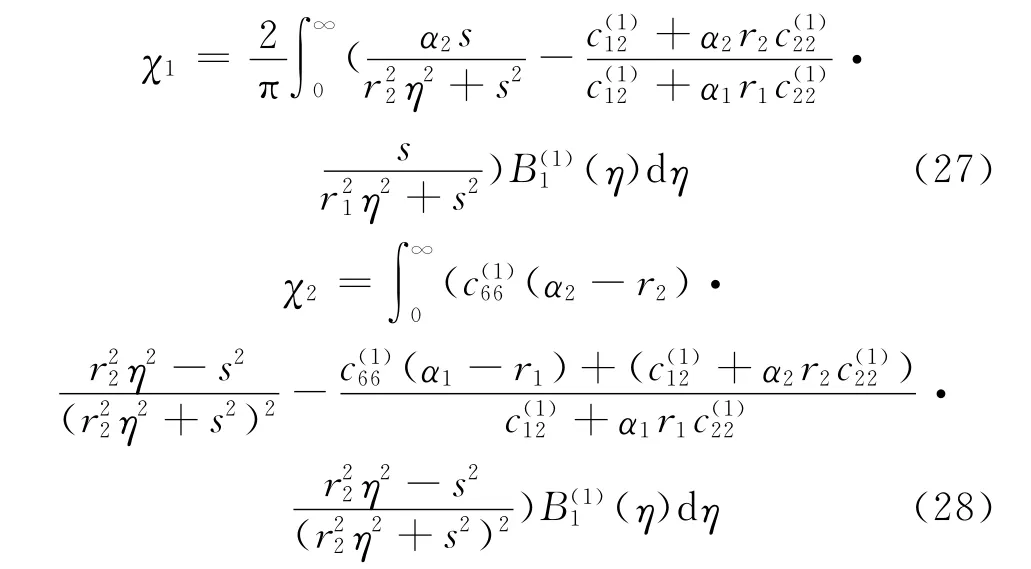
根据方程（19），（21），（25），（26），未知函数可以用关于χ1，χ2的表达式来表示，即

此处，关于Mj（s）、Nj（s），j＝（1，2，3，4）的表达式省略.

由边界条件u（1）（x，0）＝0；0＜x＜a，b＜x＜∞可以得到

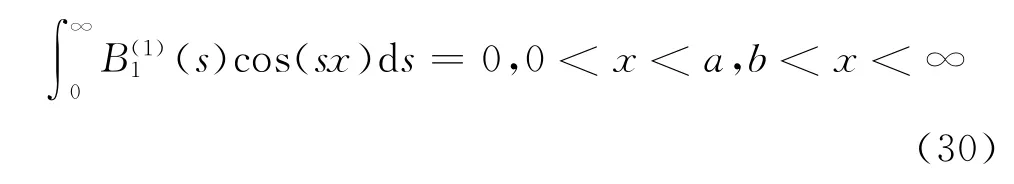
由σ（1）xy（x，0）＝－τ0，a＜x＜b把式（29）代入式（17a）～（17f）可得

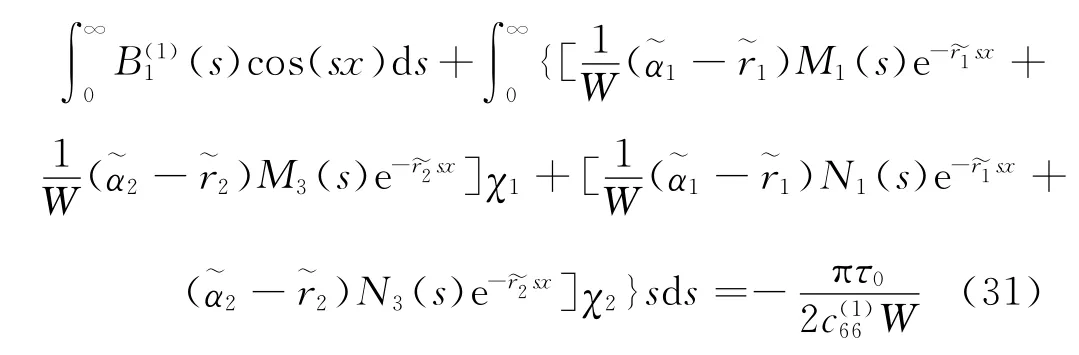
其中

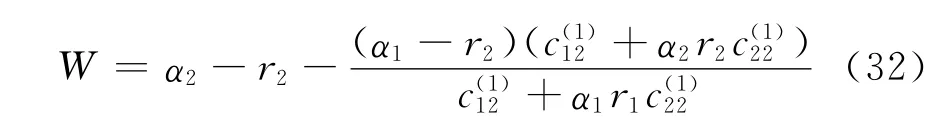
2.2 求解奇异积分方程

发现方程（31）很难求解，可以把其化成带有柯西核的奇异积分方程，然后通过数值计算得出结果.为此，定义辅助位错密度函数g（x）

这里面的系数是为了后面的计算方便而取得的，由

可得

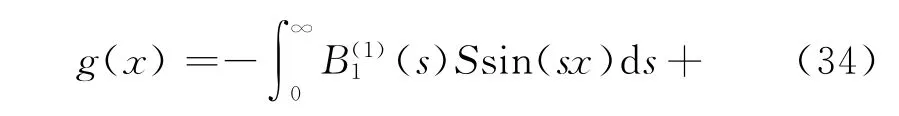
又由于u（1）（a，0）＝u（1）（b，0）＝0，则位错密度函数g（x）满足单值约束条件.

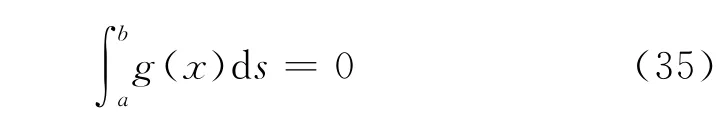
对方程（34）进行傅里叶积分逆变换，可以得到

把方程（36）代入方程（31），则方程可以转化成

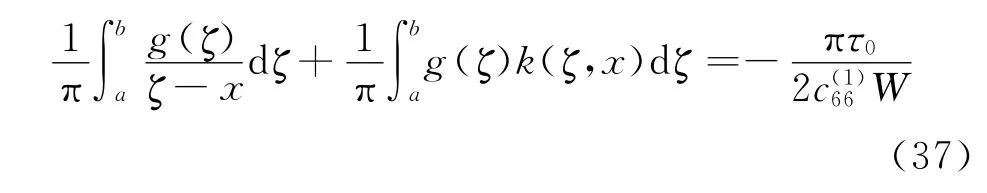
其中

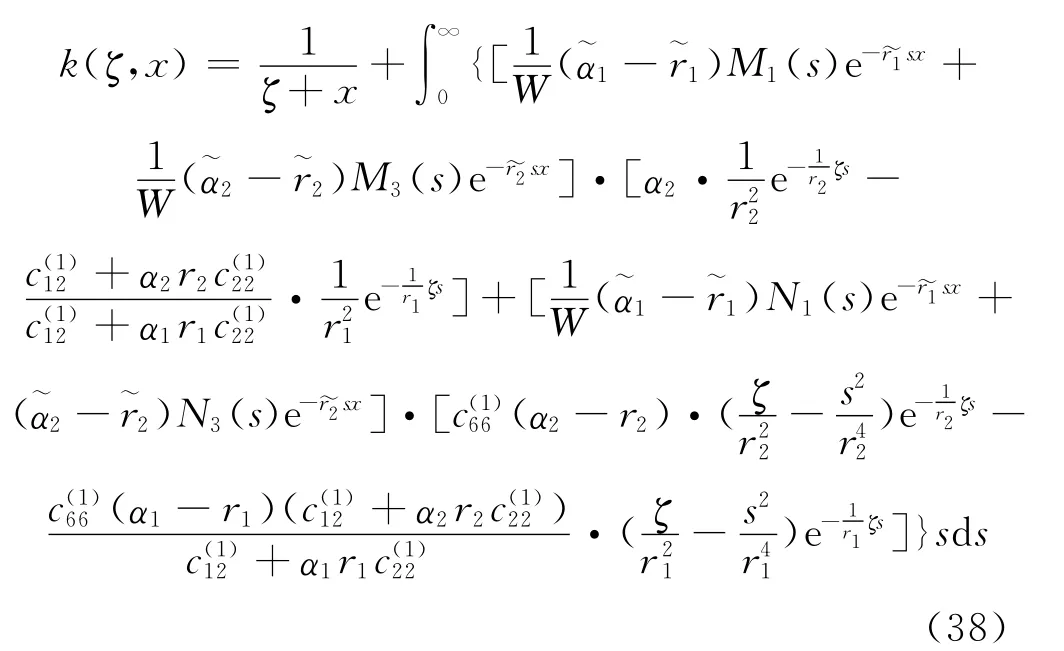
从上面分析可以看出奇异项被提出且核k（ζ，x）变得连续.而方程（37）的求解相当困难，除非核k（ζ，x）对于特殊的情况具有非常简单的表达式.对于一般情况，引入无量纲变量如下

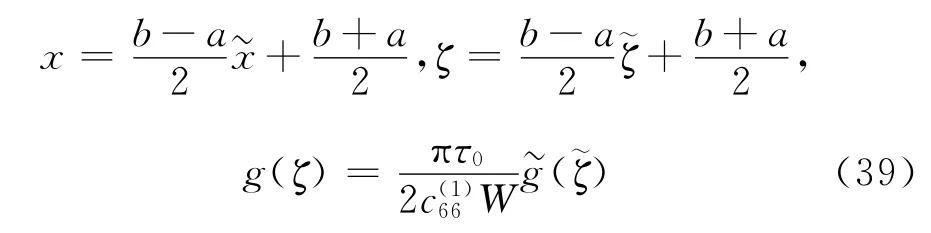
可以把方程（37）写为

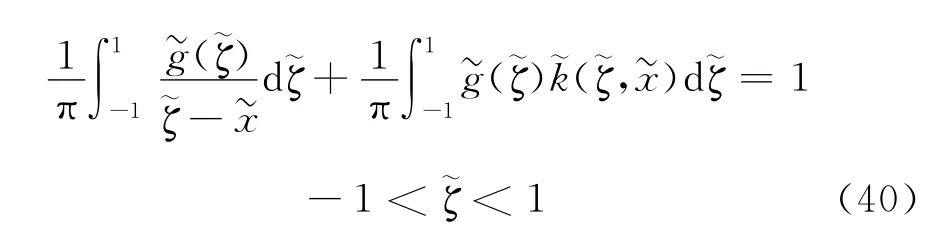
此处

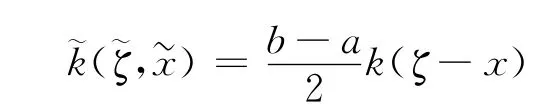
另外，从物理学的观点根据裂纹尖端的奇异反平方根，很容易地选取函数且

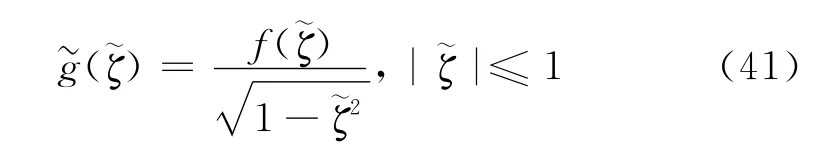
接下来用切比雪夫配置方法把方程（40）离散成一个线性代数方程组

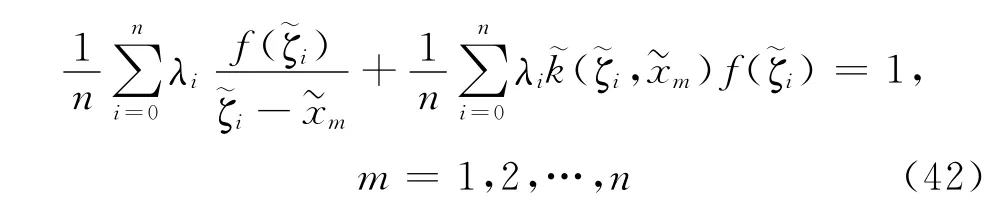
这里

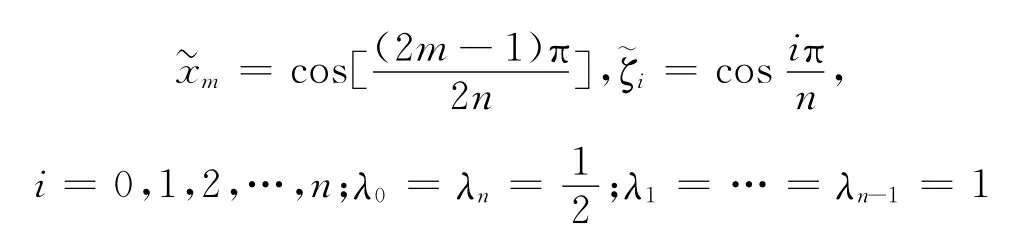
另外单值约束条件可以写为

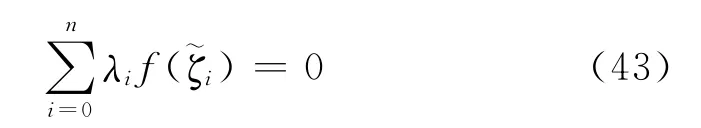
一旦线性方程组（42）、（43）的解确定了，就很容易得到裂纹尖端应力场.

3 应力强度因子

从断裂力学的观点来看，应力强度因子是一个关于裂纹尖端应力场非常重要的参数表征.

根据目前的研究定义裂纹尖端左右端的应力强度因子如下

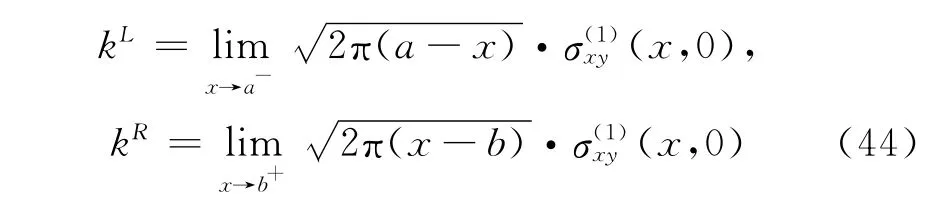
由式（41）可以得到

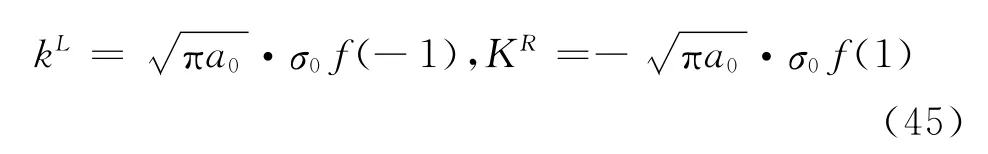
现在来看一种特殊的情形，即当正交异性材料1与正交异性材料2为同一种材料时.即

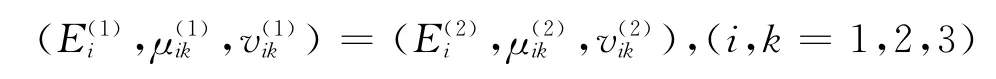
此时，经过计算可以得到：k（ξ，x）＝0而且奇异积分方程（37）可以被表示为

由式（45）很容易计算出在裂纹尖端左右端的应力强度因子为与已知结果文献［5]中保持一致.

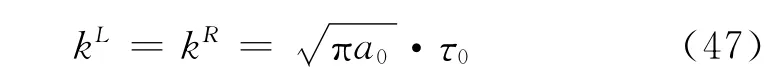
此文中的应力强度因子除了自身的材料性质影响之外，由式子（39）～（41）、（45）可以看出：裂纹长度的大小2a0即（b－a）、以及裂纹中心距双材料界面的距离c即都会对应力强度因子产生影响.

4 结 论

1）构造出正交异性双材料界面端新的力学模型.

2）通过傅里叶积分变换很巧妙地构造出了裂纹尖端的位移场，并推导出相应的裂纹尖端应力场.

3）给出了文章中所提模型中裂纹的应力强度因子表达式，并当两种材料完全相同时得出与已知文献一致的结论.

［1]Bogy D B.Two Edge－bonded Elastic Wedges of Different Materials and Wedge Angles under Surface Tractions［J].ASME Journal of Applied Mechanics，1971，38：377－386.

［2]Cook T S，Erdogan F.Stresses in Bonded Materials with a Crack Perpendicular to Interface［J].International Journal of Engineering Science，1972，10：677－697.

［3]Zhong X C，Li X F，Lee K Y.Analysis of a Mode－I Crack Perpendicular to an Imperfect Interface International［J].Journal of Solids and Structures，2009，46：1456－1463.

［4]Fan T Y.Foundation of Fracture Mechanics［M].Jiangsu Sci－Tech，Nangjing（in Chinese），1978.

［5]Zhang X S.A Central Crack at the Interface between Two Different Orthotropic Media for the ModeⅠand ModeⅡ［J].Engineering Fracture Mechanics，1989，33（3）：327－333.

［6]周振功，王 彪.位于两不同正交各向异性半平面间张开型界面裂纹的性能分析［J].应用数学和力学，2004，25 （7）：887－1000.