基于LS－DYNA的大跨度弧形闸门船舶碰撞有限元分析

牛文宣 胡友安 沈安磊

（河海大学 机电工程学院，江苏 常州 213022）

近年来，随着经济的飞速发展，水路运输能力日益提高，船舶的航行数量和航行速度都在不断增加.但是，由于某些通航船舶的速度快、舵效低，闸门遭遇船舶碰撞的事故时有发生，给正常的水上航运、水工建筑物和闸门等带来了一定的安全隐患，造成经济损失，甚至人员伤亡.

一大型水利工程主要功能是挡洪、排涝、蓄水、引排水，控制内江水位和水质，满足特殊船只通航和连通引航道两岸的交通要求.为此，设计了由一个40m宽中孔和7个20m宽侧孔节制闸，以及一个20m宽副孔非标准船闸.中孔大跨度弧形工作闸门跨度40 m，高8.5m，闸门底槛高程1.5m，门顶高程9.89m.闸门采用卧式液压启闭机，全水头动水启闭，为目前国内跨度最大的弧形闸门，图1为闸门的安装布置图.作为该大型水利工程中主要通航道中的闸门，为了确保其安全性能，防止闸门在通航时的碰撞损坏，必须对闸门被船体碰撞后的损坏情况进行分析仿真，为闸门的设计、制造、维护和维修提供理论参考依据.

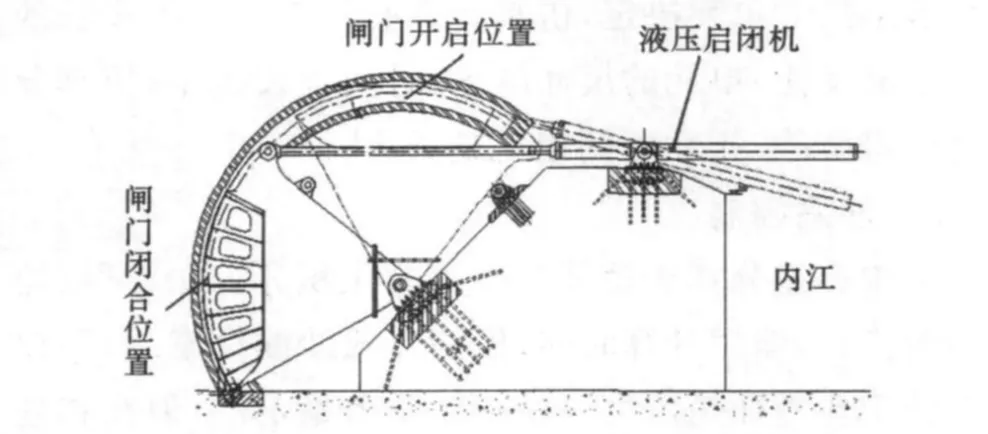
图1 大跨度弧形闸门安装布置图

图2为该闸门的三维结构模型图，闸门的门体结构采用空间板梁结构，门体有面板、主梁、纵隔板以及支臂等部件组成.闸门面板所在圆弧半径为8m，面板厚为24mm，面板上设置了8根主梁和11根纵隔板，支臂采用箱型梁，各板梁翼缘厚度不超过24mm.

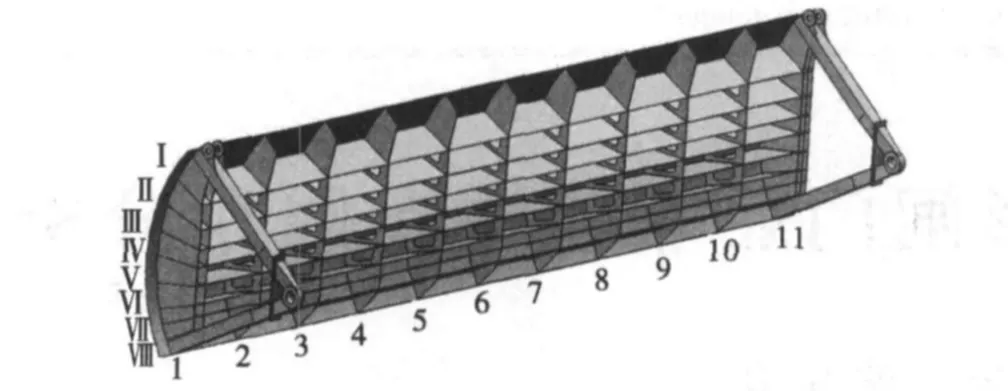
图2 大跨度弧形闸门模型

1 碰撞基本理论

在研究船舶碰撞对闸门的影响时，主要分析闸门在碰撞发生后的力学性能变化，因此忽略船舶的内部结构变形即视为刚性体.由于船舶碰撞时间很短，在巨大的冲击载荷作用下碰撞区对应的部件会进入一种非线性动态响应过程，很可能超越弹性变形进入塑性变形阶段［1].

1.1 碰撞问题的研究方法

目前，闸门的碰撞问题的研究方法主要采用有限元数值仿真法.有限元分析方法是通过LS－DYNA软件对碰撞过程进行仿真分析，从而实现“虚拟碰撞”，可以比较真实地反映碰撞过程，得到准确的仿真结果.有限元仿真法碰撞的数学模型［2]为

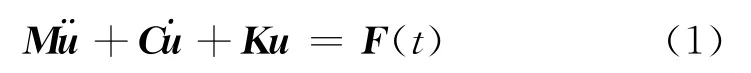
其中位移矢量u是时间t的函数，M、K、C分别为质量矩阵、刚度矩阵和阻尼矩阵，F（t）为荷载矢量.

1.2 显式中心差分算法以及时步长控制

LS－DYNA软件通过当前部件的稳定性条件控制每一时刻的时间步长，显式积分的时间步长由系统中最小尺寸单元决定，仿真计算的效率与时间步长的大小成反比，单元的尺寸越小，时间步长越小，仿真分析所需要的 CPU 时间也就越长［3，5].

1.3 沙漏控制

中心差分算法运算时采用简化积分方法，可以控制时步长，缩短计算时间，但会造成沙漏模态.沙漏模态的主要特征是产生一种在数学上稳定的，但在物理上不可能实现的状态［4].

控制沙漏的数学模型相当于在式（1）中施加一个沙漏控制力以减少或避免沙漏的产生，其公式为［1]

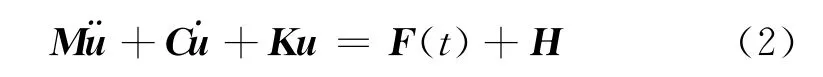
式中，H为沙漏控制力.

1.4 材料模型

弧形闸门受碰整个过程是非线性动态响应过程，受碰部件一般都要进入塑性流动阶段.因此，材料模型采用随动塑性材料模型，应变率用Cowper－symonds模型来考虑［4，6]，用与应变率有关的因数表示屈服应力

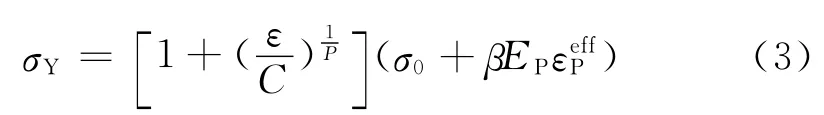
式中，σ0为初始屈服应力；ε为应变率；C，P为Cowper－symonds应变率参数；εeffP为有效塑性变形；EP为塑性硬化模量，可以由下式求解

式中，Etan为硬化模量.

1.5 接触设置

在碰撞过程中，各个接触面之间的相互作用比较复杂，可能存在不同部件之间的相互接触，甚至可能发生大变形结构自身接触现象.为了避免闸门内部各部件接触的重复定义，在闸门受碰过程中主要定义两种类型的接触：面与面的接触，闸门弧形面板为主表面，船体前部为从表面；单面接触，闸门内部的各部件间的接触均定义为单面接触，也称自接触［3].

2 有限元模型的建立

2.1 网格模型

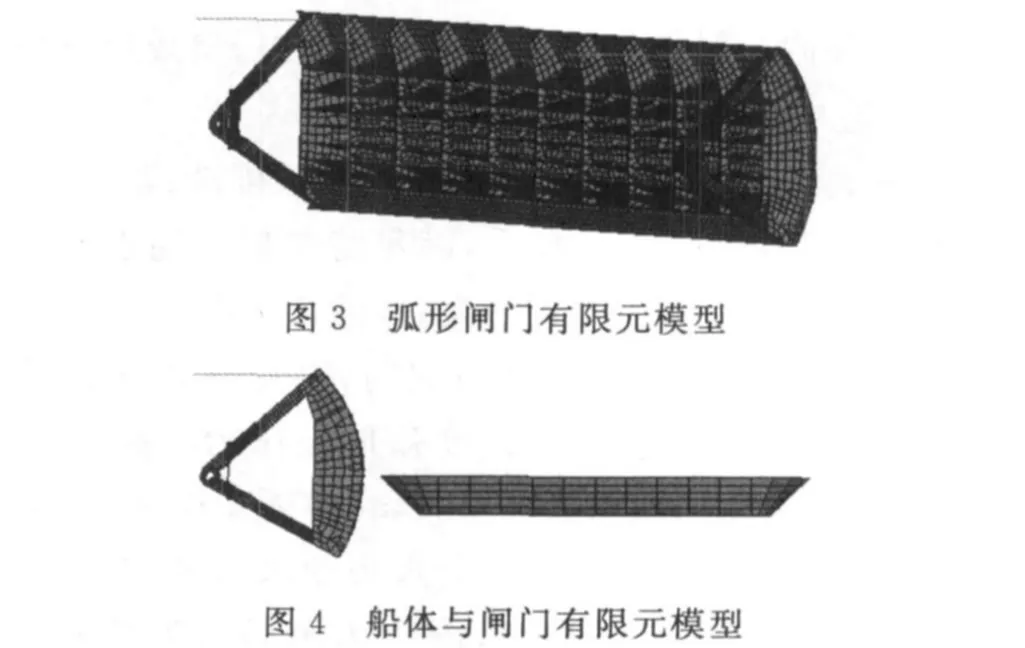
弧形闸门的所有部件均采用板壳单元拼接而得.薄壳单元采用四节点Belytschko－Tsay单元，BT单元适合于大位移和大转动，是一种最快速的显式动力学壳单元.将船体模型简化为刚体，可以大大缩减仿真分析的计算时间.采用h－adaptive方法进行自适应网格划分，使变化剧烈区的网格可以自我调整和细化，保证求解时准确的精度和分辨率［6].图3为闸门的有限元模型，图4中有船体的有限元模型.

2.2 材料参数和边界条件

BT薄壳单元中的σy取213MPa，Cowper－symonds中的应变率参数C和P分别取40.0和5.0［6]；弹性模量E为206GPa；另外，泊松比υ取为0.27；考虑到焊缝、加劲板等细部材料，取密度修正系数为1.2，密度ρ为9 120kg／m3.

在研究闸门碰撞时，考虑到文献［7]内河通航标准以及闸门实际运行要求，对弧形闸门的支铰施加约束，限制除转动自由度外的所有自由度，闸门下部与底槛相接.假设闸门在闭合状态遭受1 200t船舶的撞击，撞击高程：5.8m；撞击位置：闸门中部，Ⅳ号主梁与6号纵隔板相交处对应的弧形面板位置；船舶重量：1 200t；撞击速度：10m／s，相当于船舶19.4节的航速；碰撞方向：与水流方向相同.

3 数值仿真结果及其分析

采用显示动力学分析程序ANSYS／LS－DYNA仿真模拟整个碰撞过程.利用LS－PROPOST对结果进行后处理，可以详细了解整个碰撞过程.

3.1 弧形闸门碰撞的应力－时间曲线和应变－时间曲线

图5为碰撞应力云图，由图可知，主梁与纵隔板的应力值分布在588.9～786.2MPa之间，最大值为982.4MPa，位置发生在6号纵隔板中部，远远超过了钢材的许用应力；碰撞位置上的弧形面板受撞击的应力值分布在197.5～588.9MPa之间.

图5 碰撞应力云图（单位：Pa）

结合图6碰撞处弧形面板的应力－时间变化曲线可知，闸门碰撞应力在0.475s时达到最大.弧形面板的应力最大值为547.9MPa.然后闸门回弹，应力逐渐减少，说明闸门部分部件还处于弹性变形阶段，未发生弹性变形的部件发生回弹，也会造成碰撞处的应力值波动，其最终应力值大约在270MPa附近，已经超过了钢材的允许应力值213MPa（钢材的安全系数为1.1）.

图6 碰撞处弧形面板的应力－时间曲线

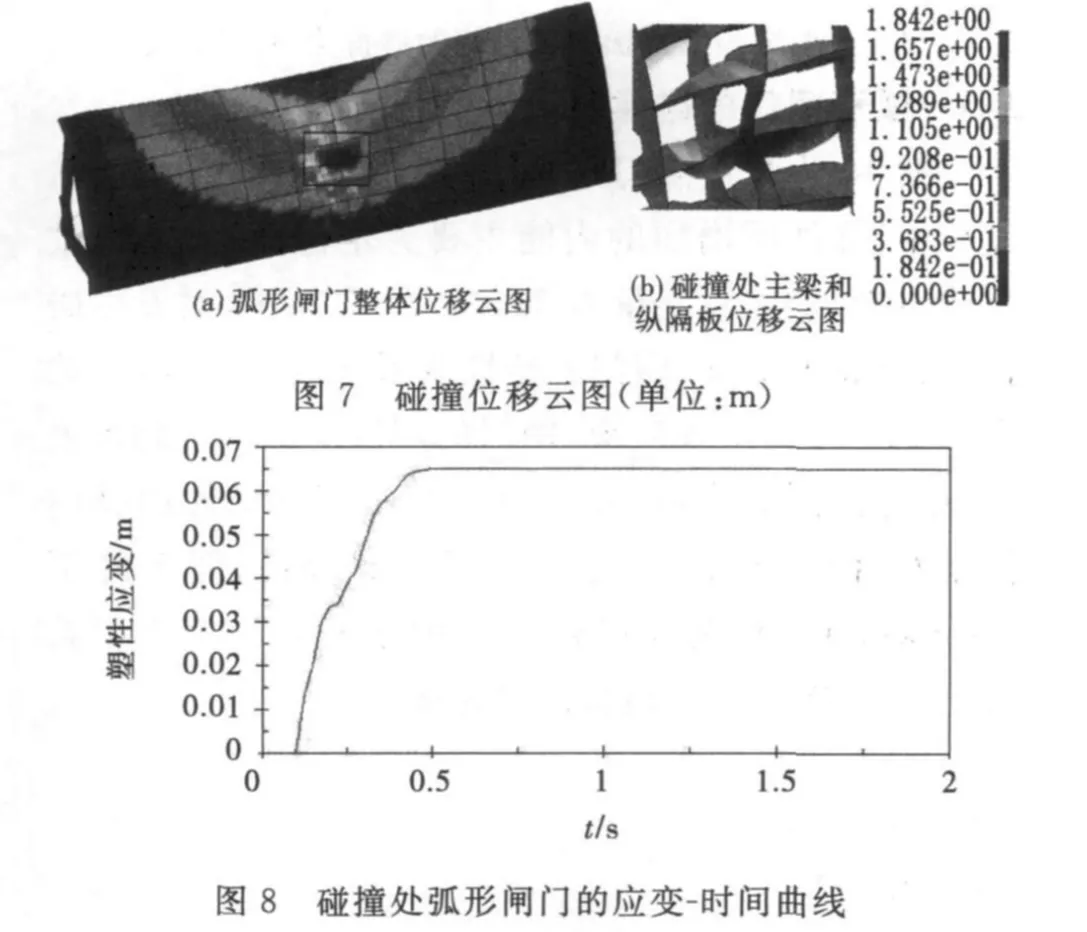
图7为碰撞位移云图.由图可知，碰撞处部件位移变形较大；闸门闭合时下部与底槛相接，因此，闸门的上部变形大于闸门的下部变形；由于闸门跨度较大，中部变形高于两边.图7中，闸门各部分的变形与实际设想一致，仿真结果正确.图8是应变－时间曲线，由图可知，闸门碰撞处的应变值在0.475s后基本不再发生变化，说明0.475s时弧形闸门碰撞处的塑性应变最大，其值为0.065 1m.结合图6应力－时间曲线可知，在碰撞结束后，碰撞处部件已经发生了塑性变形，部件的塑性变形数值不发生变化.当材料处于塑性变形阶段时，无法用虎克定律进行解释，因此，闸门的应力－时间曲线和塑性应变－时间曲线在碰撞结束后形状不同.

3.2 弧形闸门的碰撞力曲线

弧形闸门发生碰撞时，确定碰撞力的大小对弧形闸门的分析和研究有很重要的作用，图9为碰撞力－时间曲线，分别列出了船体与弧形面板的接触面上x、y和z方向以及总的碰撞力曲线，以便对闸门的碰撞力与时间的变化关系进行说明.x方向为水流方向，取水流方向为负向；z方向为平行闸门方向；y方向为竖直方向，以向下为负向.图中显示x方向的最大碰撞力为25.5×106N，方向与水流方向相同；y方向，即竖直方向的最大碰撞力为17.5×106N，方向向下；z方向，即平行闸门方向的碰撞力有3个峰值，分别为0.394×106N、－0.417×106N和－0.500 3×106N.x方向为船体的运动方向，相比其他两个方向，对闸门的撞击力主要来自这个方向，因此，弧形闸门x方向的力略高于y方向，远高于z方向的撞击力.由图9（d）总撞击力图可知，在0.475s时，闸门碰撞合力最大，其值为31.0×106N.

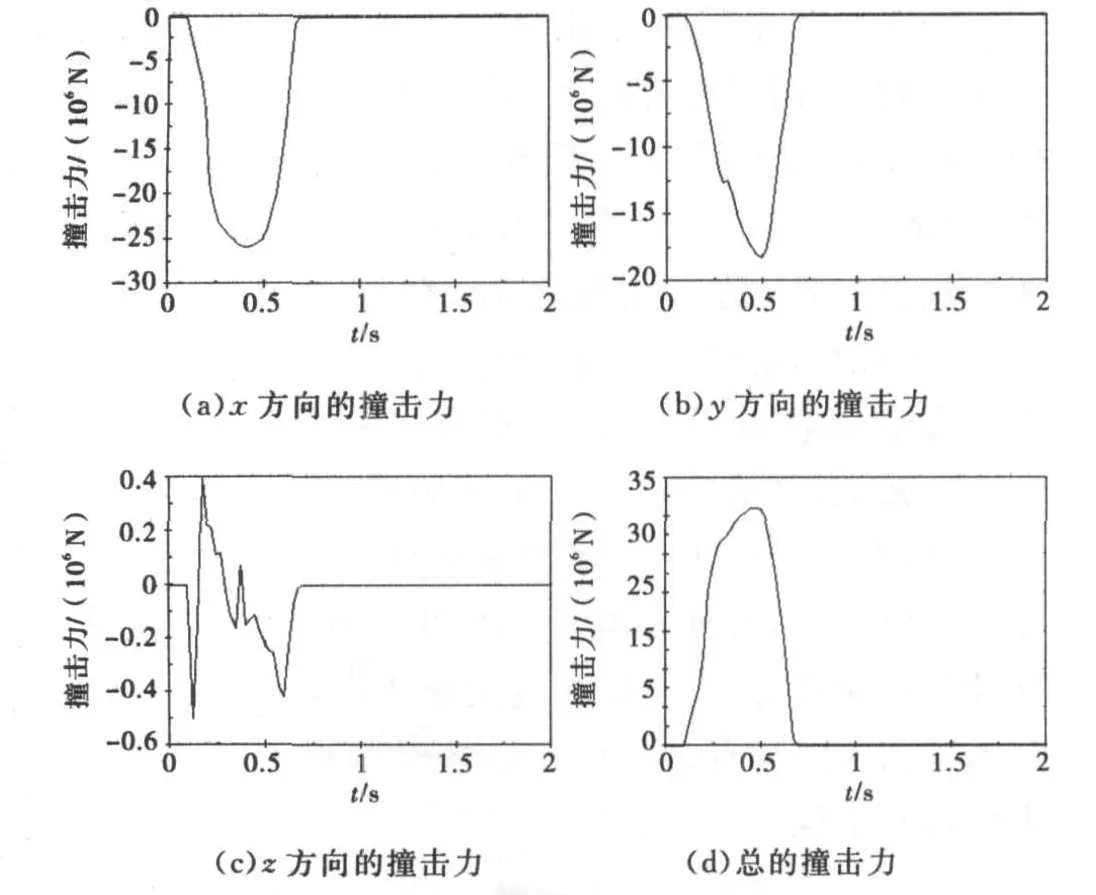
图9 船体与弧形面板接触面的碰撞力－时间曲线

3.3 弧形闸门的碰撞能量时间曲线

图10为弧形闸门的碰撞能量－时间曲线，在碰撞过程中，部件所增加的内能主要为塑性变形能，通过曲线可知，船的总能量为60 500kJ，在0.1s时发生碰撞，动能急速下降，闸门的塑性变形能迅速上升，大约在0.475s时，碰撞完成，闸门的塑性变形能达到最大值，动能降到最小值，随后由于闸门部分部件回弹内能略有降低，最终达到了55 793kJ，而动能下降至3 608kJ，沙漏能为1 113kJ，其中沙漏能的值小于总塑性变形能的5%，模拟结果正确［2].

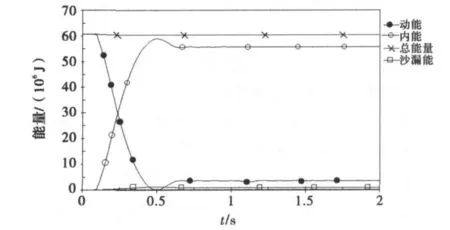
图10 弧形闸门碰撞能量－时间曲线

图11为闸门各部件能量－时间曲线，通过图11中的曲线可以知道，闸门的纵隔板、主梁以及弧形面板的塑性变形能增加较多，远高于闸门其他部件的变形.其中，主梁的变形最大，其塑性变形能已达到了24 782kJ，其次是弧形面板，其塑性变形能为21 764 kJ，纵隔板的塑性变形能为8 030kJ.根据各个能量的变化数值，主梁的变形较大，吸收动能较多，占总塑性变形能的44.4%；弧形面板吸收能量仅次于主梁，占总塑性变形能的39%；纵隔板的变形相比前二者较小，占总变形能的14.4%.

图11 弧形闸门各部件能量－时间曲线

4 结 论

基于显式有限元方法，利用ANSYS／LS－DYNA对船体碰撞弧形闸门进行了仿真分析，得到了弧形闸门受碰的应力、应变曲线和撞击力、能量曲线.从曲线可知，仿真过程基本真实反映了闸门受碰时可能出现的破坏情况，并根据碰撞力曲线和碰撞能量曲线对闸门所受到的碰撞力以及各部件的变形程度进行了分析.

闸门的受碰问题要引起重视，在碰撞过程中，碰撞的能量主要被闸门的主梁、弧形面板和纵隔板吸收，三者均产生了较大的变形，在碰撞点处，均存在较大的应力值，远高于材料的许用应力，建议对大跨度低水头弧形闸门设置防撞区，防撞区采用加厚钢板以确保闸门的安全运行［8].

［1]王自力.船舶碰撞损伤机理与结构耐撞性研究［D].上海：上海交通大学，2000.

［2]胡友安，王 孟.水工钢闸门数值模拟与工程实践［M].北京：中国水利水电出版社，2010：12.

［3]何 涛，杨 竞，金 鑫.ANSYS10.0／LS－DYNA 非线性有限元实例指导教程［M].北京：机械工业出版社，2007.

［4]殷华涛，张 海，田翠翠.船舶撞击桥墩防撞钢套箱有限元数值模拟分析［J].北方交通.2009，12：33－36.

［5]时党勇，李裕春，张胜民.基于 ANSYS／LS－DYNA 8.1进行显示动力分析［M].北京：清华大学出版社，2005.

［6]王政平，施 泉，李林友.船舶－船闸钢闸门碰撞的非线性数值仿真［J].中国科技论文在线，2007（9）：1－5.

［7]中华人民共和国交通部.GB50139－2004.内河航道通航标准［S].北京：中国计划出版社，2004.

［8]孙成智，曹广军，王光耀.为提高低速碰撞性能的汽车保险杠吸能盒结构优化［J].汽车工程，2010，12：1093－1101.