一种射流振荡式微通道流量计的设计与仿真

刘世刚，谢代梁

（中国计量学院 计量测试工程学院，浙江 杭州 310018）

近年来，随着微加工技术和微机电系统（MEMS）的发展，特别是生物医疗、化学分析和实验室研究等领域的发展对微小流量的测量需求日益凸显［1，2］.目前，流量传感器的研究已从传统的宏观尺度扩展到微观尺度，对微通道内流体流量的测量已经成为当今流量测量技术的一个重要课题.因此，新型微流量传感器的研究为解决这一问题提供了有效途径.

微尺度下液体的流动特性有别于宏观流动，特别是随着尺度的减小，流体的表面力和通道壁面对流体流动的影响愈加显著，所以宏观流体的流量测量技术无法简单地移植到微流体中［3，4］.随着微流量测量技术研究的不断深入，传统流量传感器在测量微流量的精确性和稳定性方面得到很大改善，也促进了新型微流量传感器的出现和实用化.目前，微流量测量的方法主要有差压式流量测量［5］、传热式流量测量、热线风速仪［6］等.上述的测量方法已广泛应用在工业领域，它们的测量原理各不相同，但各自都有一定的局限性.尤其是它们都通过测量微小流量引起的直流电流或电压信号来测量流量，由于微流量信号固有的信噪比低，往往无法测量极小流量.而射流振荡式传感器具有流体放大作用，特别适合极小流量的测量.因此，本文提出一种利用射流振荡原理来测量微通道内液体流量的方法.通过建立流量测量模型，利用FLUENT流体仿真软件进行数值仿真与研究.

1 射流流量计的工作原理

1.1 射流的附壁效应［7，8］

当流体由喷嘴喷出形成射流束时，由于射流的卷吸作用，会带走两侧静止的空气.为了补充因卷吸作用带走的空气，流体通过左侧狭窄的流路流速相对于右侧要快一些.

图1 射流附壁效应示意图Figure 1 Wall attachment effect of the jet

当射流两侧的附壁面对称时，由于射流自身的紊乱特性，主射流或依附于左侧壁，或依附于右侧壁，从而形成稳定的附壁射流，见图1.

1.2 射流的振荡［9－11］

射流振荡式流量计是利用附壁效应（又称康达效应）形成的双稳元件，射流振荡的基本原理，如图2.

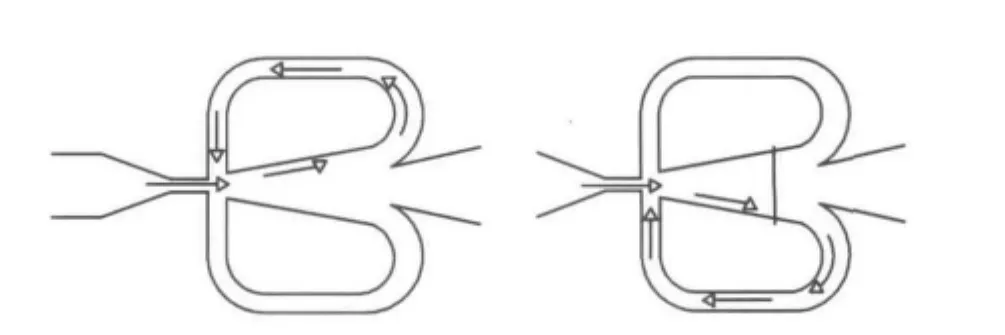
图2 射流振荡式流量计的振荡原理Figure 2 Schematic of the fluidic oscillation

由于射流的附壁效应，当流体经射流喷嘴喷出，进入振荡腔形成主射流时，射流将发生偏转并可随意依附在任一个顺流件的侧壁面上.而来自侧壁面的部分流体在出口阻力的作用下进入反馈通道，通过反馈出口垂直作用于主射流，主射流随之发生切换而依附在另一个顺流件的侧壁面上，在另一个回路中重复上述的反馈过程.在主射流的振荡过程中，反馈通道内会产生周期性的流体运动，并且其振荡频率与流体的流速成一定的比例关系.

根据Strouhal方程有：

式中，Sr为斯特劳哈尔数，主要取决于射流元件的几何形状和结构参数；l为特征长度，与流体振荡的振幅有关；v为射流入口的流速；f为流体的振荡频率.对于结构参数确定的射流流量计，斯特劳哈尔数仅仅与管道雷诺数Re有关.所以当流体的流速在一定的范围时，斯特劳哈尔数基本恒定，射流振荡器的振荡频率与入口流速呈线性关系.利用这个特性，射流振荡器在流量测量方面获得了广泛的应用.因此，可以通过测量射流元件中流体的振荡频率来实现微通道中液体流量的测量.

2 射流振荡式流量计的基本结构

本文对传统的双反馈射流元件的振荡腔进行了改进，设计了一种用于测量微通道内液体流量的射流振荡式流量计.射流流量计的基本结构，如图3，主要由振荡腔、顺流件、反馈通道、分流件等构成.

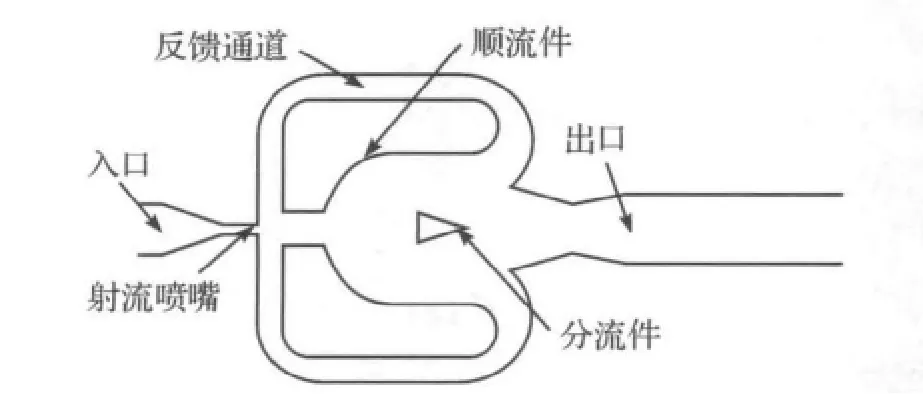
图3 射流振荡式流量计的基本结构Figure 3 Structure of the oscillating flow meter

该射流流量计的顺流件壁面被设计成凹面阶梯形，振荡腔的空间相较于传统的平面型振荡器更大，利于流体振荡行为的产生.在主射流切换的过程中，凹面上易形成一个涡流区，使附壁射流产生诱导速度，促使射流稳定地向这一侧壁面附着，从而增强了射流附壁的稳定性.

射流流量计结构的具体参数如下：入口管道管径为1mm；流体出口管径为1.4mm，以防止回流干扰；射流喷嘴长0.6mm、宽0.2mm；为减小流阻，在射流入口与射流喷嘴之间设置了30°的收缩段；位差为0.2mm，劈距为3mm；反馈通道宽度7mm，控制喷嘴宽度5mm.

3 仿真计算

3.1 预处理

本文采用计算流体力学软件FLUENT对所设计的射流振荡式微通道流量计的流动特性进行了仿真研究.为了增加求解速度，对流场做二维仿真计算.

利用FLUENT前处理软件Gambit 2.3.6对射流元件的仿真模型进行网格划分，结果如图4（a）.由于射流喷嘴以及反馈通道出口处流体的速度梯度较大，为了保证在求解速度的同时获得更好的求解精度，可以对此处网格进行局部加密处理，如图4（b）.

图4 射流元件网格划分示意图Figure 4 Schematic diagram of meshes division of the fluidic element

3.2 射流的振荡过程

以常温下的水作为流体介质，入口流速设为0.4m／s，迭代步长为1×10－4s，由迭代步长与迭代步数的乘积可以得到流体仿真过程的时间，通过数值仿真研究射流流量计的振荡过程及流量测量的基本原理.图5为流体振荡达到稳定阶段后，振荡腔内流体的流速分布在一个周期内随时间变化过程的灰度图，其中亮度越高表明流速越快，亮度越低流速越低.

当流体经射流喷嘴形成射流进入振荡腔时，由于射流的附壁效应和分流劈的共同作用，主射流随机依附在一个侧壁面上.图5表示当T＝1.200×10－1s时，主射流依附于下侧壁面.在通过出口流出时主射流的部分流体流入下反馈通道，通过控制喷嘴作用于主射流，逐渐推动主射流向上偏转.下顺流件的凹部的涡流也逐渐增强，促进了主射流的偏转，T＝1.315×10－1s时的流速分布图显示了射流向上偏转的过程；当T＝1.420×10－1s时，主射流完全依附在上侧壁面上，并有部分流体流入上反馈通道；在上控制喷嘴和上顺流件凹部的涡流作用下，主射流逐渐向下偏转，T＝1.535×10－1s的流速分布图显示射流向下偏转的过程，最终主射流又完全依附于下侧壁面，完成一次完整的流体振荡过程.

图5 振荡过程中射流元件内流体的流速分图Figure 5 Flow velocity fields of the fluidic oscillator in the process of the fluidic oscillation

从图6中可以看出，在射流振荡的一个周期内，射流流量计振荡腔内的压力变化也随时间呈周期性变化，其中亮度越高表明压力越大，亮度越低压力越小.

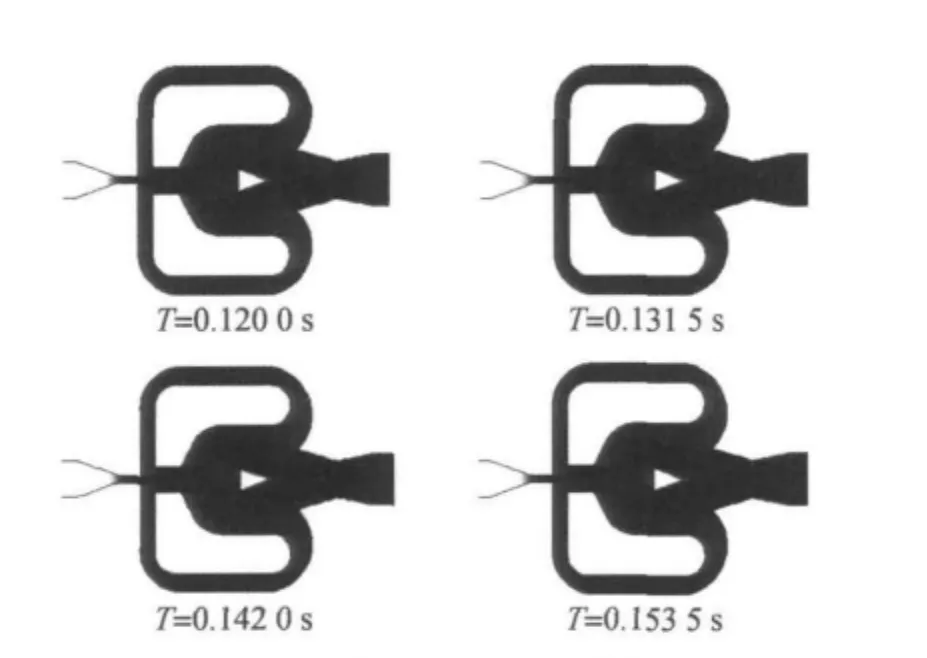
图6 振荡过程中射流元件内流体的压力分布图Figure 6 pressure fields of the fluidic oscillator in the process of the fluidic oscillation

在给定时间步长的求解过程中，射流会以一定的时间周期交替依附射流元件的上下两个侧壁面上，反馈通道内流体流速以此周期循环变化，所以我们可以通过测量射流元件的振荡频率来求得射流入口的流速.

3.3 流量测量原理

通过在上下反馈通道的直管段中分别设置监测面1和监测面2，可以在数值仿真过程中监测流过该面流体的平均流速和压力，图7和图8分别表示流速和压力随时间的变化曲线.

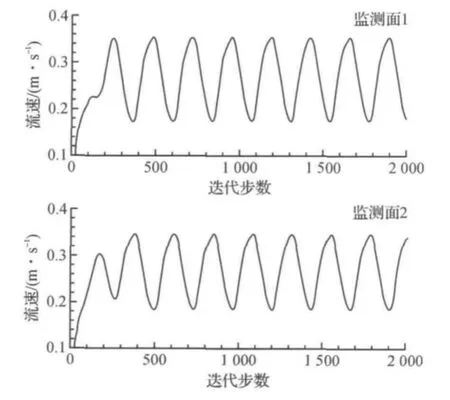
图7 入口流速为0.4m／s时，反馈通道内监测面的流速变化曲线Figure 7 Average flow velocity of the monitoring surface in the feedback channel when inlet velocity is 0.4m／s

由图7可以看出，当迭代达到300步后，反馈通道内流体的流速随时间呈周期性变化，并且上下两个监测面的流体流速变化相位相差180°.

而反馈通道内的压力也以同样的周期稳定振荡，其中上反馈通道内监测面1的压力变化如图8.通过读取时间步长和迭代步数，可以获得射流振荡的周期或频率.因此，可以建立流体流速与射流振荡频率的关系，通过测量振荡频率来实现微通道液体流量的测量.

图8 入口流速为0.4m／s时，上反馈通道内监测面的压力变化曲线Figure 8 Pressure signal of the monitoring surface in the feedback channel when inlet velocity is 0.4m／s

表1表明流体入口流速从0.1m／s按梯度增至4m／s，各流速下流体的振荡频率与斯特劳哈尔数.

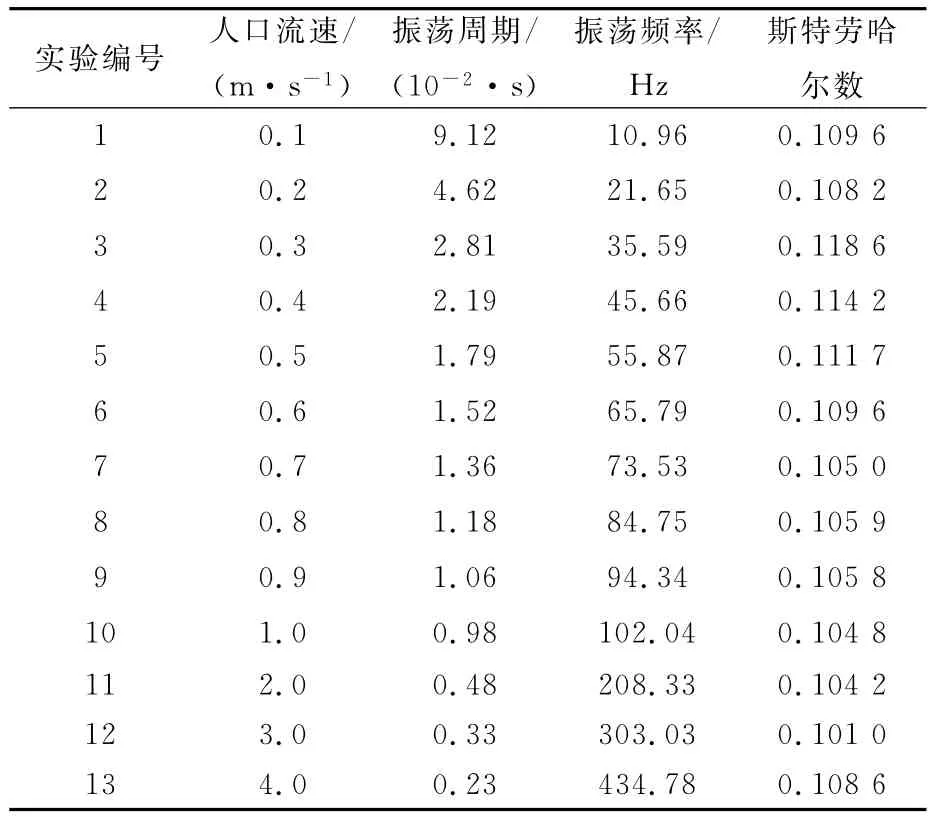
表1 不同入口流速下，射流振荡的周期、频率和斯特劳哈尔数Table 1 Period，frequency and strouhal number of the fluidic oscillation at different flow velocities

根据表1可以得到斯特劳哈尔数数与入口流速的关系，如图9.当入口流速在0.1～4m／s的范围内斯特劳哈尔数数在0.11左右附近波动.

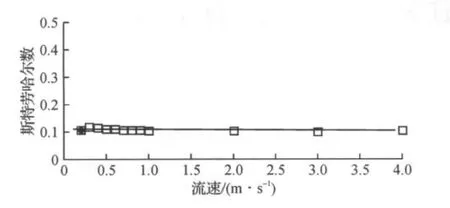
图9 Strouhal数随入口流速的变化Figure 9 Variation of the Strouhal number with the flow velocity ranges

流体流速与振荡频率的关系如图10.当入口流速在0.1～4m／s的范围内时，流体的振荡频率与入口流速具有良好的线性关系.仿真实验也发现，而当流体流速减小到0.1m／s以下时，流体的流速与振荡频率不再具有良好的线性关系.所以，通过测量反馈通道内射流的振荡频率来实现微通道液体流量的测量是可行的，但是还需要进一步优化射流振荡器的结构参数，使其在更低的流速下，流速与振荡频率间也具有较好的线性关系.

图10 射流流量计流速与振荡频率的关系Figure 10 Relation between the flow velocity and the oscillation frequency

4 结 语

本文在传统射流流量计的基础上，通过改变射流振荡器的振荡腔，设计了一种用于微通道液体流量测量的射流振荡式流量计.通过FLUENT流体仿真，对射流元件模型的流量特性进行研究，验证了射流附壁诱发流体振荡，进而优化结构参数，建立了振荡频率与入口流速的特性关系.仿真结果表明，在一定的入口流速范围内，该射流流量计内的流体振荡稳定，射流切换灵敏，斯特劳哈尔数数基本恒定，振荡频率与流速具有较好的线性关系.

［1］蔡昌武.微小流量仪表性能及其应用［J］.石油化工自动化，2009，45（4）：1－5.

［2］彭杰纲，周兆英，叶雄英.基于MEMS技术的微型流量传感器的研究进展［J］.力学进展，2005，35（3）：361－376.

［3］凌智勇，丁建宁，杨继昌，等.微流动的研究现状及影响因素［J］.江苏大学学报：自然科学版，2002，23（6）：1－5.

［4］陶 然，权晓波，徐建中.微尺度流动研究中的几个问题［J］.工程热物理学报，2001，22（5）：575－577.

［5］OOSTERBROEK R E，LAMMERINK T S J，BERENSCHOT J W ，et al.A micromachined pressure／flow－sensor［J］.Sensors and Actuators A：Physical，1999，77（3）：167－177.

［6］蔡昌武，热式液体质量微流量仪表［J］.石油化工自动化，2010，67（4）：67－68.

［7］杨永印，孙伟良，徐金超，等.附壁式双稳射流元件的设计［J］.液压与气动，2010（2）：62－64.

［8］LEE G B，KUO T Y，WU W Y.A novel micro－machined flow sensor using periodic flapping motion of a planar jet impinging on a V－shaped plate［J］.Experimental Thermal and Fluid Science，2002，26（5）：435－444.

［9］LUA A C，ZHENG Z S.Numerical simulations and experimental studies on a target fluidic flowmeter［J］.Flow Measurement and Instrumentation，2003，14（2）：43－49.

［10］周云波，林加端.射流流量计的原理及发展［J］.中国仪器仪表，1997（1）：3－5.

［11］WANG H，BECK S B M，PRIESTMAN G H，et al.Fluidic pressure pulse transmitting flow－meter［J］.Chemical Engineering Research and Design，1997，75 （4）：381－391.