矩形柱二维尾流的稳定性研究

刘 喆，邵传平

（中国计量学院 计量测试工程学院，浙江 杭州 310018）

钝体绕流是流体与结构相互作用中的常见问题之一，广泛存在于桥梁与隧道建设、海洋平台、航空航天等工程实际应用中.当流体以一定速度流过钝体时，会在钝体尾部形成规则的漩涡脱落，致使面两侧的压力分布交替变化，不仅造成结构的疲劳损伤，而且当旋涡脱落频率与结构固有频率接近时还会产生共振［1］，造成直接破坏.因此，对钝体尾流进行分析，有可能揭示漩涡脱落和尾流演化的机理，并且探索在不同外激发形式下系统的发展规律，为主动控制提供理论依据［2，3］.

自从一些理论工作者将绝对和对流不稳定性的概念应用于钝体尾流的研究以后，圆柱绕流线性稳定性方面的研究［4-6］已进行得相当广泛.Triantafyllou［7-8］对时均流场的速度剖面分析表明，直至圆柱底部5倍半径的下游，流动是绝对不稳定的，再往下游流动变成对流不稳定了.Monkewit［9］对拟合的实验尾迹速度剖面分析表明，绝对不稳定区域在Re数约为临界值一半时已经出现.Yang和Zebib［10］采用谱方法、孙德军［11］采用低维Galerlin方法对计算得到的圆柱定常尾迹流场分析表明，在Re＝20附近是局部绝对不稳定性已经出现，在此Re以下，流场是整体稳定的和对流不稳定的.随着Re数的增大，绝对不稳定区域逐渐增大.邵传平［12］进行了亚临界雷诺数圆柱尾流稳定性实验，发现对近尾流进行脉冲扰动后，能够激发出不衰减的旋涡脱落现象，实验还发现扰动位置在圆柱后一定范围内才有效，再向下游方向则扰动随时间衰减.由此说明圆柱近尾流中存在一个绝对不稳定区域.

对于矩形柱体尾流的情况，长宽比为5∶1的研究相对较多［13-17］，在本文中，我们针对长宽比为3∶1的矩形柱进行了实验与数值模拟两种方法的研究.

1 实验装置与方法

实验在水槽中进行.实验段长100cm，宽20cm，高20cm.矩形柱由硬塑料制成，柱体长20cm，宽度为B＝1cm，厚度为L＝3cm（长度与宽度之比为3∶1）.矩形柱横跨实验段，柱轴位于实验段截面中心，两端紧贴水槽竖壁，为防止水自由表面的影响，在水槽上端盖有一有机玻璃板，总长100cm.水槽实验时，给流场施加瞬时扰动的装置是一根外径为0.15cm，内径为0.1cm的不锈钢管，从水槽上壁沿纵剖面垂直插入水槽.插入水中的长度小于0.2cm，使细不锈钢管本身不会对流场产生的干扰.细管上端通过塑料管与一洗耳球连接.将洗耳球固定在一定高度，使其内外压力保持平衡，当给其一瞬时压力，一股细流通过细管射入流场，对矩形柱尾流形成扰动.实验中采用荧光彩液显示方法，在矩形柱前端设置一个开口，将调配好的彩液导入到矩形柱的凹口处，使彩液能够在水流的作用下绕着矩形柱流动至柱体后端.在激光发生器的作用下拍摄实验效果，实验装置，如图1.

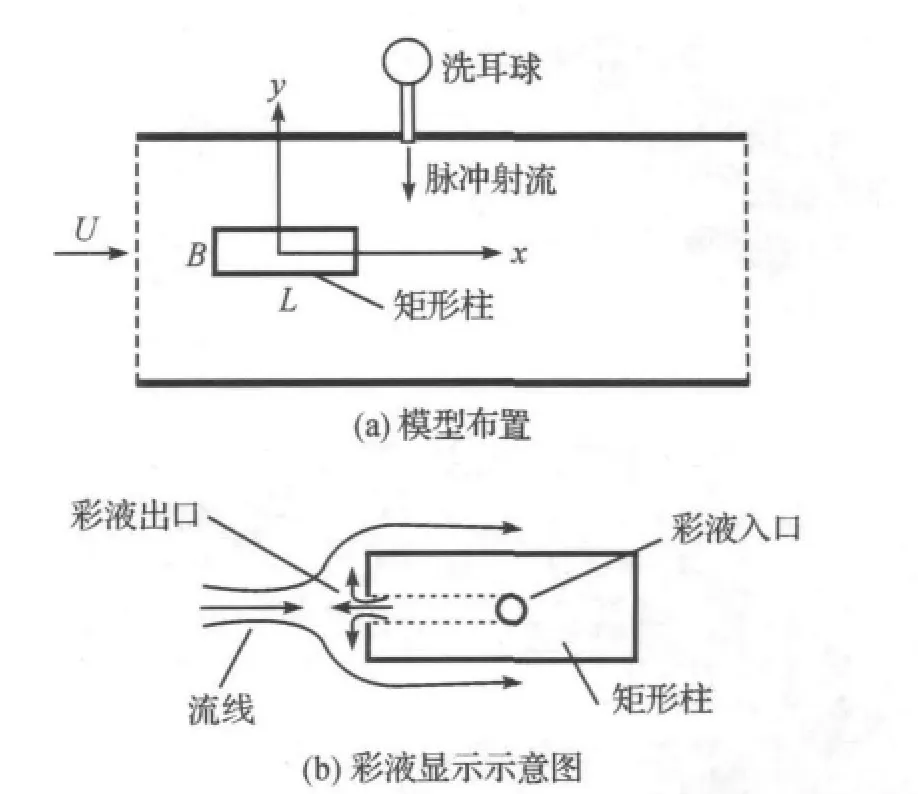
图1 模型及实验设备布置Figure 1 Arrangements of cylinder model and experimental device

2 实验结果与讨论

当雷诺数很小时，矩形柱绕流没有旋涡脱落产生，只有当雷诺数处于临界值时才能发生规则的旋涡脱落现象.将来流流速由0缓慢上升到一定值U后保持不变，使得U所对应的雷诺数小于临界雷诺数，从而得到静态基本流.为了验证尾流的绝对不稳定性和对流不稳定性，我们在尾流的3个不同站位用上述方法对静态基本流施加瞬时脉冲扰动，来观察尾流流态的变化.如果脉冲扰动能够激发出不随时间衰减且持续时间很长的旋涡脱落，则该扰动点是绝对不稳定的；反之，如果扰动不能激发出不衰减的旋涡脱落，则该扰动点是绝对不稳定的.

图2为矩形柱宽B＝1cm，长L＝3cm，Re＝80的实验结果.脉冲扰动位置在流向X／B＝1.0，展向Z／B＝5.5处.在t＝0～120s时间范围内为未扰动时的静态基本流，此时速度脉动很小.在t＝120s时施加一个瞬时脉冲扰动，激发出了较强的旋涡脱落，并且该旋涡脱落一直保持着非常大且稳定的扰动状态，直到t＝720s后才逐渐有减弱迹象.

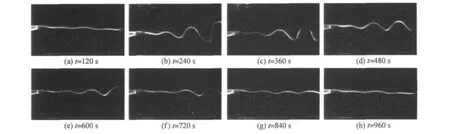
图2 在X／B＝1.0，Z／B＝5.5处施加短时脉冲射流扰动后的尾流脉动衰减情况，Re＝80Figure 2 Decay process of wake fluctuation induced by an impulse jet disturbance applied at X／B＝1.0，Z／B＝5.5，Re＝80

图3为Re＝82时的实验结果.脉冲扰动位置在流向X／B＝－10.0，展向Z／B＝5.5处.在t＝0～120s时间范围内为未扰动时的静态基本流，此时速度脉动很小.在t＝120s时施加一个瞬时脉冲扰动，能够激发出较强的旋涡脱落，扰动随时间放大，直到t＝960s后仍无明显减弱迹象.

图3 在X／B＝－10.0，Z／B＝5.5处施加短时脉冲扰动后的尾流发展情况，Re＝80Figure 3 Evolution of wake fluctuation induced by an impulse disturbance applied at X／B＝－10.0，Z／B＝5.5 Re＝80

图4为Re＝75～85之间的实验结果.脉冲扰动位置在流向 X／B＝20.0，展向Z／B＝5.5处.在t＝0～120s时间范围内为未扰动时的静态基本流，此时速度脉动很小.在t＝120s时施加一个瞬时脉冲扰动，只有微弱的振荡现象产生，无法激发出旋涡脱落.在t＝240s就开始减弱直至消失，持续时间很短.

图4 扰动后X／B＝20.0，Z／B＝5.5处脉动衰减情况，Re＝80Figure 4 Decay process of wake fluctuation induced by an impulse disturbance applied at X／B＝20.0，Z／B＝5.5 Re＝80

由水槽实验中的大量事实说明，在临界雷诺数情况下，当不加任何扰动时，尾流是稳定的，没有出现旋涡脱落现象.当Re＜75时，则无论在上游或是下游任何地方施加脉冲扰动，扰动都会衰减.随着雷诺数的增大，扰动所激发的旋涡脱落衰减所需要的时间加长，至Re＝80附近时，经过600s，旋涡脱落才逐渐减弱.当在柱体上游和下游靠近柱体位置处施加一个瞬时脉冲扰动时，扰动随时间放大，并出现旋涡脱落现象，并且这种扰动激发的旋涡脱落可以持续很长时间，不会衰减.发现在下游较远处施加同样的脉冲扰动时，不会在柱体后面激发出旋涡脱落.说明矩形柱近尾流中存在一个绝对不稳定区域，在该区域内扰动将在当地放大，经过复杂的演化，最后形成不衰减的旋涡脱落.

3 数值方法及边界条件

本文主要求解Re＝79.5时的脉冲扰动矩形柱尾流的情况，此时为层流，其控制方程为二维非定常不可压N－S方程，表示如下

式（1）中：u，v—流体的纵向和横向速度；ρ—流体密度；t—时间；x，y—坐标轴；p—流体压力；μ—流体粘性系数.

采用有限体积法对上述方程进行求解，采用Galerkin有限体积法进行离散，对于式中的非线性项通过分离时间步长法进行处理，压力与速度耦合采用SIMPLEC算法，时间步长0.025s，扰动时间步长0.00025s，扰动持续时间1s，扰动入口宽度b／B＝0.04.计算域采用非均匀四边形网格，矩形柱和脉冲口附近采用较密集网格，计算域边界采用较稀疏网格.总网格数在260000以上.

边界条件：

1）入口边界 入口流向速度U＝3.2mm／s，脉冲射流出口速度u＝50～200mm／s；

2）出口边界 采用自由边界条件；

3）固壁 采用无滑移边界条件.

图5 数值模拟网格及扰动射流出口附近网格图Figure 5 Sketches of mesh over the whole domain and mesh in the vicinity of jet outlet

4 计算结果与分析

定义矩形柱的宽为B，长为L，来流速度为U，脉冲速度为u.为保证流场充分发展，计算区域为60B×24B的矩形区域.

4.1 临界Re数的确定

图6显示了数值模拟的矩形柱尾流中的流线图和涡量图，雷诺数范围为79～85.数值模拟结果表明：在Re＝79时流动是稳定的，没有旋涡脱落生成；在Re≈79.5时，流动由稳定转向不稳定；在Re＝85时，在尾流区域内出现明显的旋涡脱落.因此，Re≈79.5即为数值模拟的临界Re数.

4.2 扰动强度

本文所讨论临界雷诺数流动的稳定性问题是非线性的，与扰动强度有密切关系，只要当扰动强度达到一定阈值的时候，才会产生失稳.

根据图7可以看出，相同条件下脉冲扰动速度与来流速度比值分别为0、15.6、31.2、62.4四种情况旋涡生成的大小和位置都有明显变化.

4.3 绝对不稳定区域

根据图8中的数值模拟结果，在临界雷诺数下，在柱体上游X／B＝－10.0、X／B＝－4.0、柱体近尾流区域内的X／B＝1.0、X／B＝6.0位置处进行脉冲扰动，都能够将静态尾流激发为持续不衰减的旋涡脱落状态.在柱体下游X／B＝10.0位置处进行脉冲扰动，不能激发旋涡脱落现象.这说明在临界雷诺数条件下，在柱体近尾流中存在一个绝对不稳定区域，在远离柱体下游尾流区，流动是对流不稳定的.

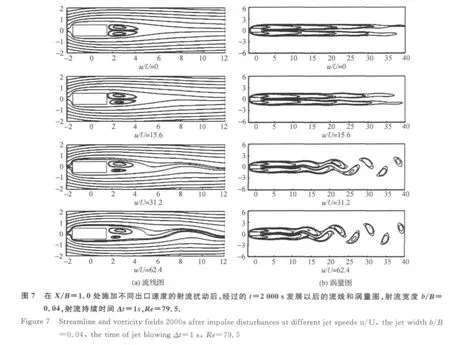
图8 不同站位处施加脉冲射流扰动后经过t＝2000s的发展以后的的流线图和涡量图，射流宽度比b／B＝0.04，射流速度比u／U＝31.2，射流持续时间Δt＝1s，Re＝79.5Figure 8 Streamline and vorticity fields 2000seconds after impulse jet disturbances applied at different X／Bstations，the jet width b／B＝0.04，jet speed u／U＝31.2and time of jet blowingΔt＝1s，Re＝79.5.

5 结 语

本文采用实验和数值模拟相结合的方法对长宽比为L／B＝3的矩形柱尾流在临界雷诺数附近（Re＝UB／v＝79～85，其中，U 为来流速度，v为流体运动粘度）的稳定性问题进行了研究.当雷诺数接近临界值时，尾流对小扰动的增长指数接近于零，在很长时间内尾流处于二维定常状态.此时在柱体上游或近尾流一定位置沿着垂直于来流方向施加宽度很小的短时脉冲射流后，能够迅速激发出规则的旋涡脱落，并能够持续很长时间不衰减.但是，如果在远尾流区某位置施加同样的扰动，则不能激发持续的旋涡脱落.研究发现当扰动强度较小（脉冲射流宽度比b／B＝0.04，脉冲射流出口速度比u／U＝15.6）时，即使在近尾流区施加扰动，也不能激发持续的旋涡脱落.当脉冲射流宽度比保持b／B＝0.04不变，扰动射流出口速度增大为u／U＝31.2时，当在区域（12＜X／B＜10）内施加横向扰动时，均能够激发旋涡脱落.以上结果表明，临界雷诺数附近矩形柱体尾流中存在一个绝对不稳定性区，该区域内的有限幅值扰动将会迅速发展放大，并演化为旋涡脱落；而且尾流具有很强的非线性效应，旋涡脱落状态受扰动强度的影响很大.

［1］WILLIAMSON C，GOVARDHAN R.Vortex－induced vibration［J］.Annual Review of Fluid Mechanics，2004，36：413－455.

［2］ROCKWELL D.Sympon nonsteady fluid dynamics［J］.Fluid Mech，1990，12：379－394.

［3］童秉纲，崔尔杰.现代流体力学进展［M］.北京：科学出版社，1991：25－55.

［4］OERTEL H.Wakes behind blunt bodies［J］.Annual Review of Fluid Mechanics，1990，22：539－564.

［5］HANNEMANN K，OERTEL H.Numerical simulation of the absolutely and convectively unstable wake［J］.Fluid Mech，1989，199：55－88.

［6］HUERRE P，MONKEWITZ P.Local and global instabilities in spacially developing flows［J］.Annual Review of Fluid Mechanics，1990，22：473－537.

［7］TRIANTAFYLLOU G，CHRYSSOSTOMIDIS C.On the formation of vertex streets behind stationary cylinders［J］.Fluid Mech，1986，170：461－477.

［8］KARNIADIKIS G，TRIANTAFYLLOU G.Frequency se－lection and asymptotic states in laminar wakes［J］.Fluid Mech，1989，199：441－469.

［9］MONKEWITZ P.The absolute and convective nature of instability in two－dimensional wakes at low Reynolds numbers［J］.Phys Fluids A，1988，31：999－1006.

［10］YANG X，ZEBIB A.Absolute and convective instability of a cylinder wake［J］.Phys Fluids A，1989，1：689－696.

［11］孙德军.钝体尾迹的稳定性分析及控制［D］.合肥：中国科技大学，1995.

［12］邵传平，鄂全学，王 薇.圆柱尾流的绝对不稳定性［J］.力学学报，1999，31（1）：1－9.

［13］PROVANSAL M，MATHIS C，BOYER L.Benard－von Karman instability：transient and forced regimes［J］.Fluid Mech，1987，182：1－22.

［14］MATSUMOTO M，SHIRATO H，ARAKI K.Spanwise coherence characteristics of surface pressure field on 2－D bluff bodies［J］.Journal of Wind Engineering and Industrial Aerodynamics，2003，91（1，2）：155－163.

［15］BRUNO L，FRANSOS D，COSTE N.3Dflow around a rectangular cylinder：a computational study［J］.Annual Review of Fluid Mechanics，2010，98（6，7）：263－276.

［16］MANNINI C，SODA A，SCHEWE G.Unsteady RANS modelling of flow past a rectangular cylinder：Investigation of Reynolds number effects［J］.Computers and Fluids，2010，39（9）：1609－1624.

［17］MANNINI C，SODA A，SCHEWE G.Numerical investigation on the three－dimensional unsteady flow past a 5：1 rectangular cylinder［J］.Journal of Wind Engineering and Industrial Aerodynamics，2011，99（4）：469－482.