基于响应阈值的群机器人地图创建探索策略

阎 静，曾建潮，张国有

(太原科技大学计算机科学与技术学院，复杂系统与计算智能实验室，太原030024)

随着群智能研究的发展，群机器人系统受到了越来越多研究者的关注，这主要是由于群机器人系统除了具有多机器人系统的并行性、鲁棒性和柔性等优点外[1]，还有其自身特有的优点，如机器人结构的简单性、个体数量的伸缩性和同构性等。迄今为止，群机器人研究已积累了若干基准任务[2]，如:队形分布[3]、搬运、围捕、搜索和地图创建等问题。在这些任务当中，地图创建特别引人关注，它是移动机器人导航和智能机器人真正实现自主的最重要条件之一[4]。现实生活中当地震、矿难等突发性事件发生时，需要快速获得灾难现场的准确环境信息，为救援工作赢得时间，这时群机器人地图创建就能发挥作用。机器人地图创建中有很多问题需要解决，如:测量误差的减少、问题规模的估计、地图创建的一致性问题、环境中动态事物的处理和地图创建过程中的探索策略等[5]。本文基于黄蜂群的响应阈值模型设计了一个群机器人地图创建的探索策略。

1 算法的生物学背景

群机器人研究起源于生物学的启发，通过对社会性昆虫如蚂蚁、白蚁和黄蜂等观察，人们发现这些社会性昆虫虽然个体都很简单，但通过个体之间的协作，整个群体可以完成复杂的任务，并且当它们面对多项需要完成的任务时，会自动调节资源分配和参与这些任务的个体数量[6]，这一现象被Bonabeau等人用黄蜂群响应阈值模型来解释，描述为公式(1)。在公式(1)中S是与某一任务相关的刺激强度，响应阈值θ是一个内部变量，对S做出响应，可以通过公式(1)计算出任务被执行的概率[7]。

本文基于响应阈值模型提出的探索策略很好的满足了群机器人系统的要求。群机器人系统具有以下特征:(1)该系统应该包括大量的个体[8];(2)系统没有中央协调机制，群中的机器人具有同构性[9];(3)群体中的机器人能力有限;(4)个体机器人具有有限的感知能力和通讯能力[10]。基于上述特征，算法的设计必须满足群体规模的伸缩性、个体的自治性和个体功能的简单性等要求。如果机器人携带各种传感器，如激光雷达、声纳和摄像头等设备将搜集到的相邻路径信息作为任务的刺激强度，并根据机器人自身的响应阈值就可决定对任务的参与倾向，提高地图创建的效率，同时也可满足群机器人系统的特征要求。

2 算法响应函数及前提假设

根据黄蜂群的响应阈值模型所提出的算法响应函数如下:

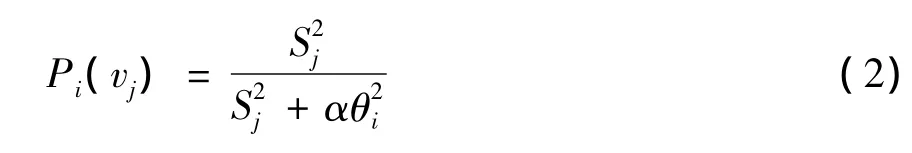
公式(2)中Sj是顶点j的任务量度相当于任务的刺激强度，θi是机器人i的响应阈值，αi是调节因子(0＜α＜1)，Sj的具体公式表示如下:

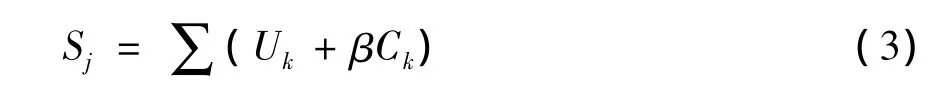
公式(3)中Uk表示顶点j的未访问路径数量，Ck表示顶点j的已访问路径数量，β表示调节因子(0＜β＜1)。由公式(2)可以看出，当机器人所在顶点的相邻顶点如果包含的未访问路径数量较多时，该顶点Sj值就大，机器人访问该顶点的概率就大;如果相邻顶点的未访问路径较少，该顶点Sj值就小，相应机器人访问该顶点的概率就小。这样机器人会以较大概率访问含未访问路径较多的相邻顶点，从而提高了地图创建的效率。

本文算法实现对机器人的功能要求如下:(1)有限感知能力:感知判断环境中的顶点和边;(2)环境顶点和边的标识能力:机器人能对工作环境中的顶点或边进行特征信息的提取和保存;(3)标识的识别能力:机器人能够对所处环境的特征信息与机器人的内部表示进行匹配;(4)全局通信能力:机器人能够进行广播通信，同时这种直接通信是异步进行的[11]，但这种通信并不用来对机器人间的行为进行协调;(5)较准确的测距能力。

机器人需要维护的信息包括:(1)所创建的地图Mat=(V，L);(2)顶点权值信息数组Value[]:保存相临顶点由公式(2)计算出的权值;(3)探测边集合E:机器人首先将探测到的顶点边进行临时标识后，存放在集合E中，这里称为临时边。

3 探索策略算法描述

3.1 机器人状态

机器人的运动是一个可离散化的连续过程，根据机器人状态的变化可分成若干关键点，将所有状态连续起来便形成一个过程[12]。本文构造了一个有限状态自动机来对单机器人的状态进行描述，有限状态自动机(finite automaton，FA)M是一个五元组:M=(Q，∑，δ，q0，F)。

有限状态自动机模型中各变量的具体实现如下:(1)状态的有穷集合Q={WaitState，Recognition-State，MarkState，MoveState，MapAdditionState，Search-State，SelectState}。集合Q由七种状态构成，分别是:等待状态(WaitState)、识别状态(RecognitionState)、标识状态(MarkState)、地图信息添加状态(MapAdditionState)、搜索状态(SearchState)、选点状态(Select-State)和移动状态(MoveState)。(2)可接受的输入集合∑ ={RecognizeVisited，RecognizeNoAccess，FindT-empEdge，FindNothing，Markdid，MapUpdate，JudgeEqual，JudgeNoEqual，MoveNewVertex，SlectNewVertex}。集合∑包含了机器人在地图创建过程中遇到的物理事件，包括:①RecognizeVisited:顶点已被访问;②RecognizeNoAccess:顶点未被访问;③FindTempEdge:有临时边被找到;④FindNothing:临时边未被找到;⑤Markdid:顶点和边都被做了标记;⑥MapUpdate:地图更新完毕;⑦JudgeEqual:集合E和集合L相等;⑧JudgeNoEqual:集合E和集合L不相等;⑨MoveNewVertex:新顶点被访问;⑩SlectNewVertex:新的访问顶点被选出。(3)转移函数δ是Q×∑→Q的一个映射，被有限状态自动机识别。(4)起始状态q0={RecognitionState}。(5)结束状态F={Wait-State}。具体状态转换图见图1。

图1 机器人有限状态自动机状态转换图Fig.1 The finite state automata state transition figure of robot

3.2 探索策略描述

结合图1对本文探索策略描述如下:机器人首先进入识别状态判断该节点是否被访问，如已被访问就进入地图信息添加状态，否则进入节点标识状态;在地图信息添加状态，机器人将节点信息和来时边的信息(包括路径长度)一起添加到所创建地图Mat=(V，L)中，加入L中的是按节点标识命名的正式边，同时修改E中的临时边改成正式边，完成后通知其它机器人进行地图信息更新;而机器人在节点标识状态会对节点和边进行标识，并将边进行临时标识后加入E中，完成后机器人进入地图信息添加状态，将顶点信息和来时边的信息(包括路径长度)一起添加到地图中，通知其它机器人进行信息更新，地图更新完毕后，机器人进入未访问边搜索状态，在此状态机器人将搜索一条临时边作为下一访问路径，此时机器人会面临三种情况:(1)机器人找到了一条临时边:机器人会进入移动状态;(2)机器人未找到临时边，但此时集合E不等于集合L:机器人会进入选点状态，机器人通过响应函数计算出相邻边的响应值，按响应值依概率选择下一条访问路径;(3)机器人未找到临时边，且集合E和集合L相等:机器人认为地图创建完成进入等待状态。当机器人进入移动状态后，机器人会移动到下一访问顶点进行访问，此时机器人会重新进入节点识别状态。

4 仿真实验

4.1 实验方案

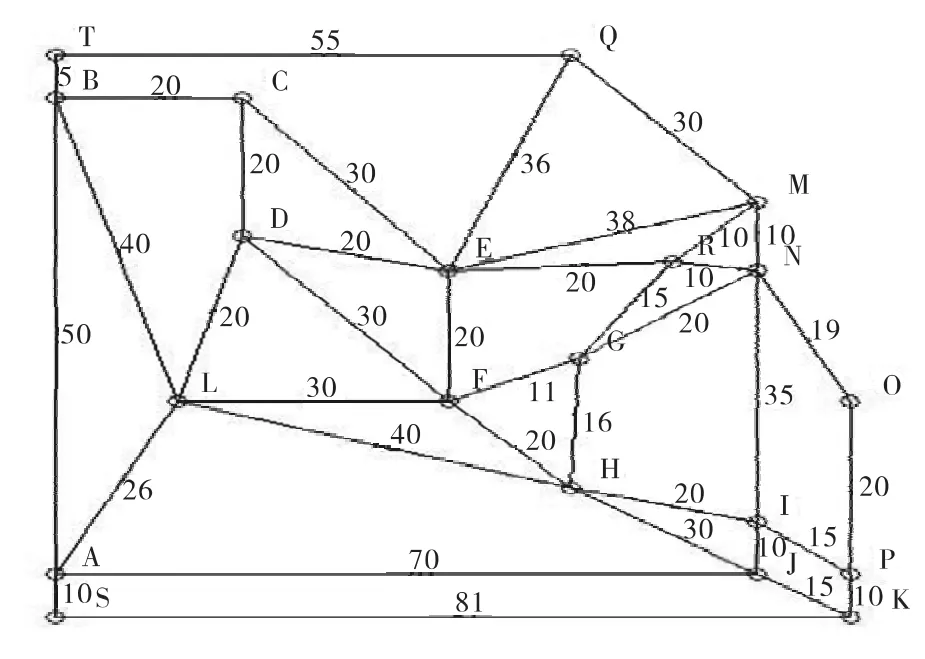
图2 群机器人地图创建仿真拓扑地图Fig.2 The building simulation topology map of swarm robot map

采用JavaSe设计的仿真平台对提出的算法进行仿真实验，用多线程模拟群机器人的并行访问，实验方案制订如下，仿真环境用带权拓扑地图描述，见图2，在该地图中共包含有20个顶点和39条边，边长一共是991个单位距离长度。实验中分别用2、4、6、8和10个数量的机器人进行实验，这里假设机器人匀速运动，运动的速度是单位距离/单位时间，实验对每个数量的机器人都进行20次实验，最后取平均值，按响应阈值的不同实验分三组进行，实验中其他参数设置如下，公式(2)中的α=0.016(0＜α ＜1)，公式(3)中的 β=0.6.

4.2 评价指标

(1)总覆盖长度:机器人在地图创建完成后所走过的路径总长度，包括机器人重复走过的路径;(2)覆盖时间:机器人完成地图全覆盖所需的时间，这里用总覆盖长度比机器人数来表示覆盖时间;(3)覆盖率:机器人所创建地图的路径长度与工作环境的路径长度之比，这里所计量的路径长度不包括重复路径。

4.3 实验结果

机器人按照不同响应阈值进行仿真实验后，将实验结果平均值列为表1和表2，表中机器人创建地图的覆盖率都是100%.

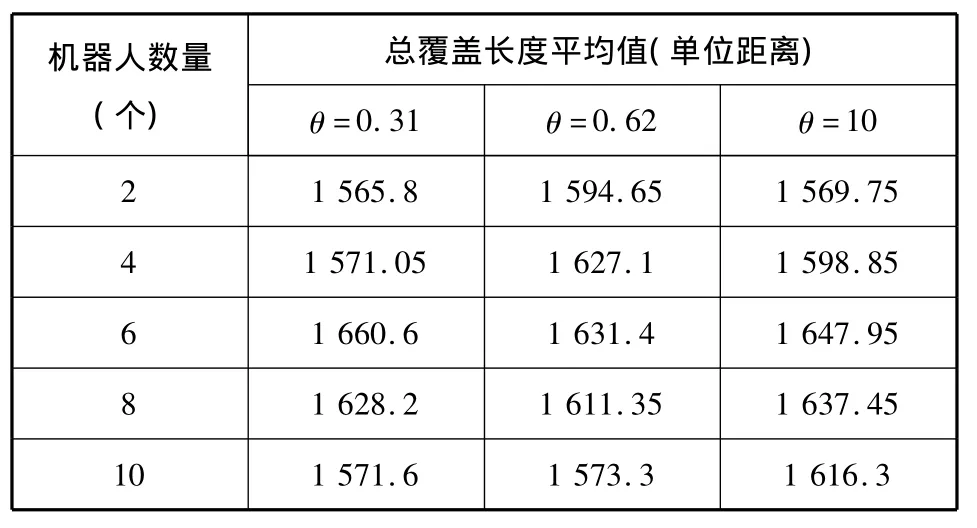
表1 20次实验总覆盖长度平均值表Tab.1 Experiment 20 times total coverage length average table

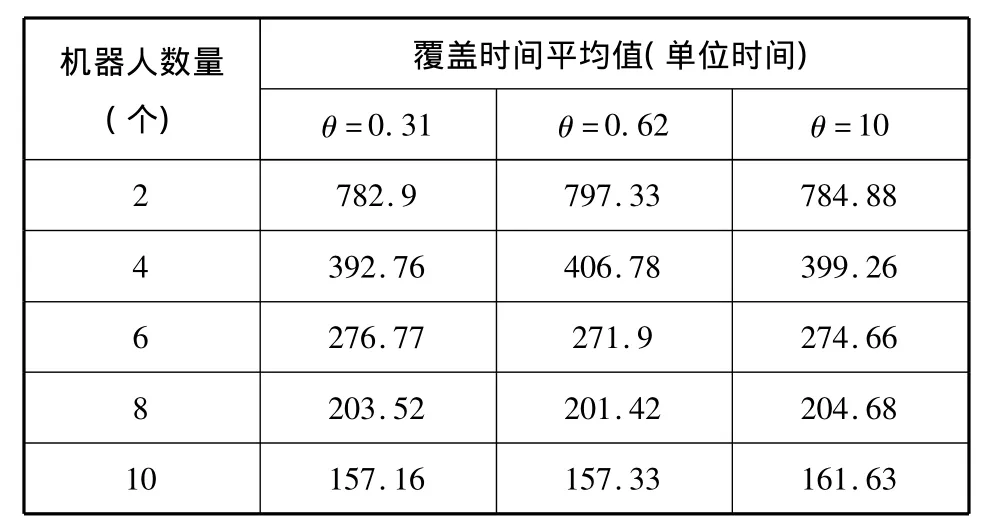
表2 20次实验总覆盖时间平均值表Tab.2 Experiment 20 times total coverage time average value table

4.4 实验结果分析

由表1可以看出当机器人数量较少时，如机器人的数量是2个或4个的时候，表中响应阈值θ=10的总覆盖长度比θ=0.31的大，却比θ=0.62的要大，这可以解释为阈值设置的大小在机器人较少数量的情况下对总覆盖长度的影响不明显，而当机器人的数量大于6个的时候，由表1可以看出θ=0.31和θ=0.62的总覆盖长度明显少于θ=10的总覆盖长度，这也可以解释为当机器人的数量较多时，响应阈值的设置对地图创建效率的影响较大，且响应阈值设置的较小时效果较好。由表2可知当机器人的响应阈值分别设置为θ=0.31、θ=0.62和θ=10时，随着机器人数量的增加，机器人地图创建所用的覆盖时间也随之下降，这说明随着机器人数量的增加，机器人整体的探索距离并没有增加，这也就是说算法满足了群机器人系统的伸缩性要求，当机器人地图创建的覆盖时间降低时，也就意味着通过增加机器人的数量，提高了群机器人创建地图的效率。

5 结论

通过实验结果可以看出，本文算法很好的满足了群机器人系统的伸缩性，实验结果表明当响应阈值设置的较小时效果较好，并且机器人的数量越多受响应阈值的影响越大。本文中的仿真实验是在一个特定的加权拓扑地图上进行的，下一步研究需要对实验地图的规模和种类进行扩充，另外算法中群机器人的探索效率还会受到很多因素的影响，如任务调节因子的设置，地图中顶点和边的数量等，以及这些参数之间的相互关系，这些都需要进一步的研究。

[1]谭民，范永，徐国华.机器人群体协作与控制的研究[J].机器人，2001，23(2):179-181.

[2]薛颂东，曾建潮.群机器人研究综述[J].模式识别与人工智能，2008，21(2):183-185.

[3]谌海燕，曾建潮.基于PSO的多机器人编队控制[J].太原科技大学学报，2009，30(5):28-31.

[4]蔡自兴，贺汉根，陈虹.未知环境中移动机器人导航控制研究的若干问题[J].控制与决策，2002，17(4):385-390.

[5]THRUN S.Robotic Mapping:A Survey[R].Technical Report CMU-CS-02-111.School of Computer Science Carnegie Mellon U-niversity Pittsburgh，USA，2002，:3-5.

[6]张国有，曾建潮.基于黄蜂群算法的群机器人全区域覆盖研究[J].模式识别与人工智能，2011，24(3):433.

[7]BONABEAU ERIC，THERAULAZ GUY，DENEUBOURG JEAN_LOUIS.Fixed Response Thresholds and the Regulation of Division of Labor in Insect Societies[J].Bulletin of Mathematical Biology，1998，60:753-756.

[8]SAHIN E.Swarm Robotics:From Sources of Inspiration to Domains of Application[C]//Proc of the SAB Workshop on Swarm Robotics.Santa Monica，USA，2004:10-20.

[9]BALCH T.Hierarchic Social Entropy:An Information Theoretic Measure of Robot Group Diversity[J].Autonomous Robots，2000，8(3):209-238.

[10]王海.群机器人技术进展[C]//中国自动化学会第二十五届青年学术年会论文集，沈阳:东北大学出版社，2010:2-4.

[11]李进，薛颂东，曾建潮，等.群机器人目标搜索中的通信模式研究[J].太原科技大学学报，2011，32(4):15-19.

[12]王旭阳，吕恬生，徐兆红，等.类人机器人复杂运动的状态转换规划方法研究[J].中国机械工程，2007，18(6):659-662.