复Finsler 流形间的调和映射

肖金秀，贺 群，陈志华，邱春晖

（1.上海工程技术大学 高职学院，上海200437；2.同济大学 数学系，上海200092；3.厦门大学 数学科学学院，福建 厦门361005）

文献[1－5]给出了实Finsler流形间的调和映射的一些开创性成果.而对于复Finsler流形的情形，基于比实Finsler流形更复杂，更不同于Hermite度量的实部即为Riemann度量，复Finsler度量的实部不再是实Finsler度量，导致复Finsler流形间的调和映射 的研究更复杂.文献[6]通过考虑∂－－能量变分研究了紧Riemann曲面到复Finsler流形上的调和映射.最近，文献[7]则通过计算能量变分和应用文献[8]中的非线性椭圆系统研究了复Finsler流形到Hermite流形上的调和映射，并且得到有关Kähler Finsler流形到复流形间调和映射的存在性定理.

本文，通过定义其上的整体内积得到相应 的伴随算子和Laplace算子，并且巧妙地给出了复Finsler度量和实Finsler度量之间的关系，得到了复Finsler流形间调和 映射的能量泛函与∂－能量泛函和∂－－能量泛函之间的关系式，并且通过技巧性的计算分别得到了他们的变分公式，从而给出了调和映射的定义；由于复Finsler流形中有关复Finsler度量的联络系数不仅和底流形上的点有关而且和纤维也有关，进而导致∂－能量与∂－－能量之差不是同伦不变的.

1 预备知识

设M为复n维的复流形，（zk）为其局部坐标，T1，0M为其全纯切丛.设u＝（zk，ηk）∈T1，0M，F（u）为强拟凸复Finsler度量，由zk＝xk＋ixn＋k和ηk＝yk＋iyn＋k知，实函数F（u）＝（xa，yb）不再是TRM＼｛0｝上实Finsler度量.若（gjk－）确定的矩阵是正定的，则称gjk－是强凸的[9].因此，Munteanu引进不同于Abate和Patrizio的方法，实的度量结构不是由决定，而是由矩阵gjk－的实部确定.

命题1[9]设（z，η）由强拟凸复Finsler度量F诱导T1，0M上的 Hermite度量 ，则L2（x，y）：＝gab（x，y）yayb为一实Finsler度量，其中g

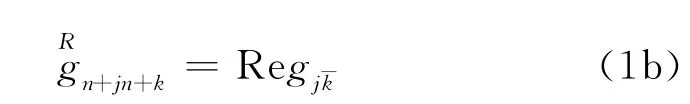
式中：Re表示实部；Im表示虚部.

称L为强拟凸复Finsler度量F诱导的实Finsler度量.设的逆矩阵，即为），由可得：

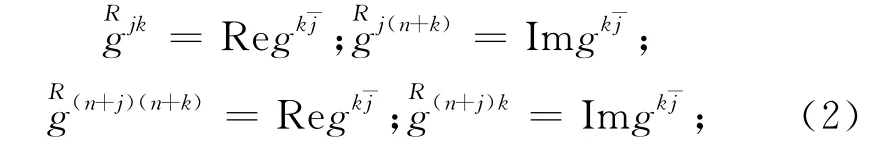
设C＊＝C＼｛0｝，射影切丛PTM定义为PTM＝／C＊且∶PTM→M，则PTM上的Finsler几何量关于切向量（即纤维坐标）是零齐次的.令∧δηn，PTM 体积形式为dV＝dτ∧d∧ dσ ∧d（参见[10－11]）.

引理1 设（M，F）为紧强拟凸复Finsler流形.则对于所有射影切丛PTM上的函数f，

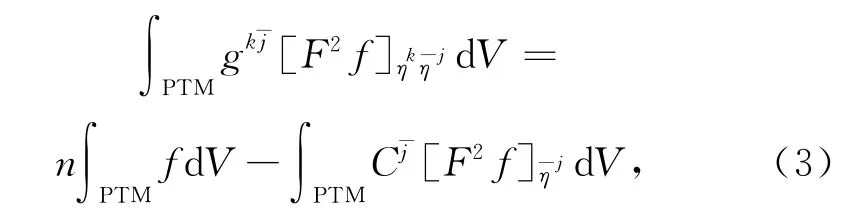
因此，

在PTM上积分得

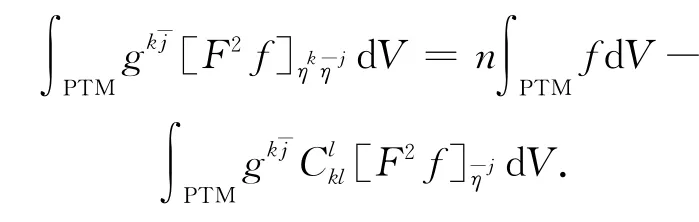
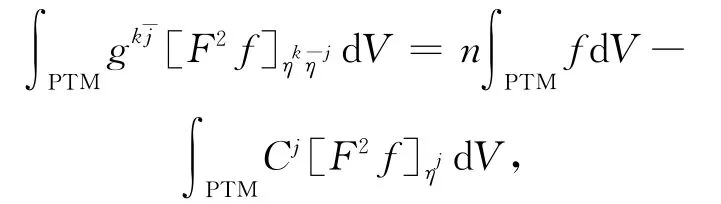
由式（3）得

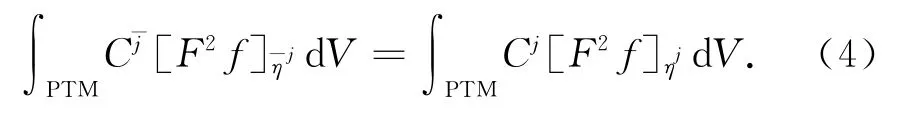
引理2 设（M，F）为紧强拟凸复Finsler流形.若T1，0M上的光滑函数f满足f（z，λη）＝λ－f（z，η），则

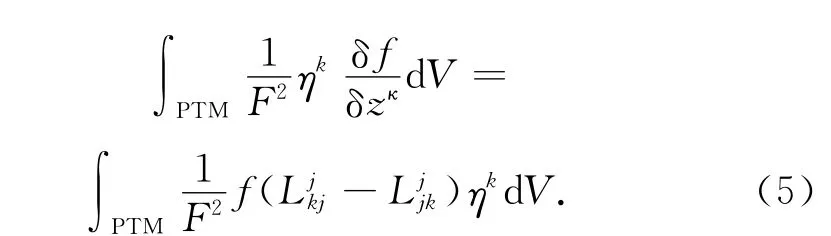
而有

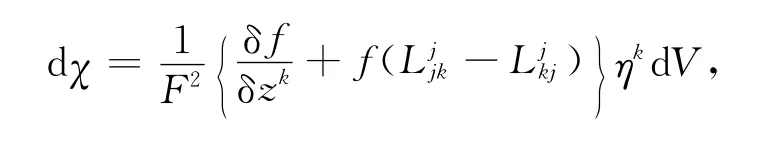
因此

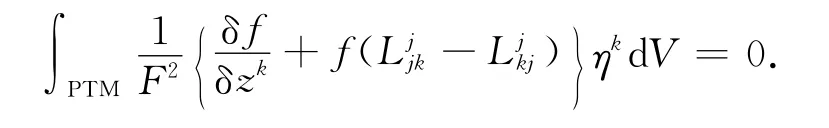
2 调和映射

设（M，F）为n维紧强拟凸复Finsler流形，（N，L）为m维强拟凸复Finsler流形.设f：M→N为非退化光滑映射.记M的局部坐标为｛zi｝以及｛ωμ｝为N的局部坐标，f局部可表示为

设有关度量F的Chern－Finsler联络的联络系数为有关度

量L的联络的联络系数为

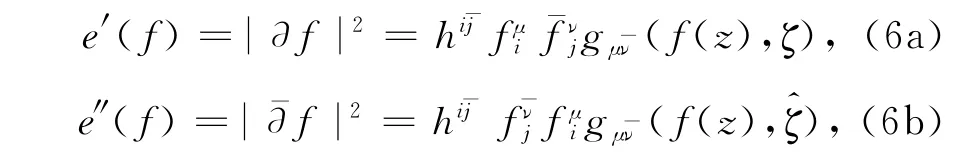
其中f既非全纯也非反全纯.否则，若f全纯则e″（f）＝0；若f反全纯则e′（f）＝0.f的∂－能量泛函和∂－－的能量泛函可定义为

由引理2，公式（6）可重写为

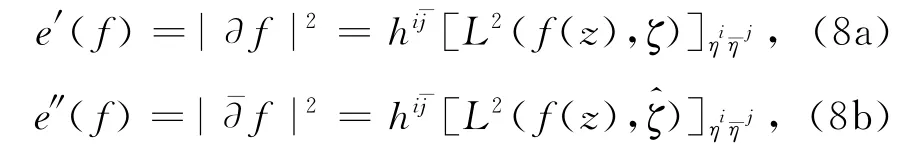
从而式（7）也可重写为

记TRM的实局部坐标为（x1，…，x2n，y1，…，y2n）及TRN的实局部坐标为（x～1，…，x～2m，y～1，…，y～2m），其中zi＝xi＋ixn＋i，ωμ＝x～μ＋ix～m＋μ，则

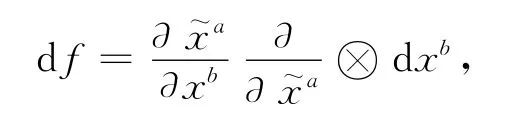
其中1≤a，…≤2m，1≤b，…≤2n且

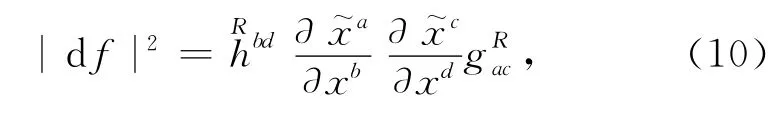
1≤a，c…≤2m，1≤b，d…≤2n.根据式（1）—（2），得

从而，f的能量密度可定义为.由式（6），（11），有

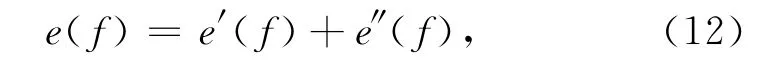
且

则，

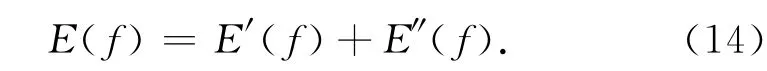
现考虑f＝f0的光滑变分，即一族光滑映射ft∶M→N，t∈D＝ ｛z∈C｜｜z｜＜ε｝.

则f的∂－能量泛函和∂－－能量泛函变分为

由变分｛ft｝诱导上的向量为

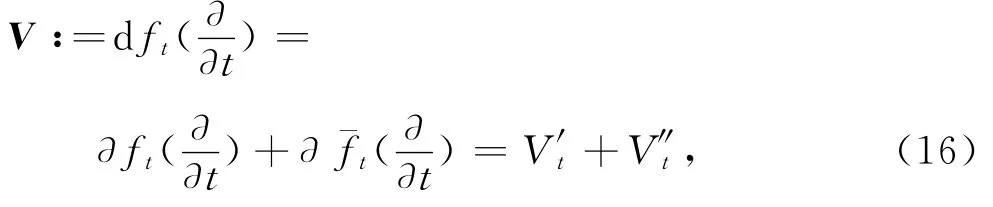
且

则

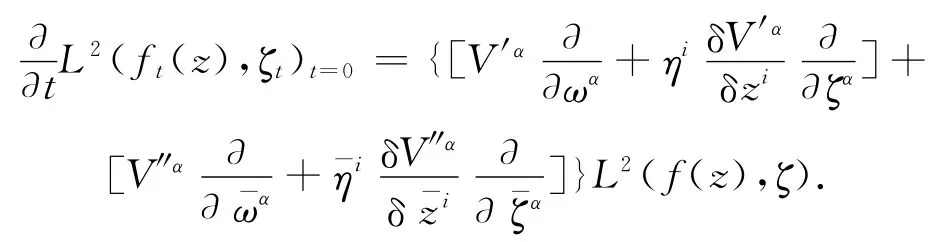
由引理2得

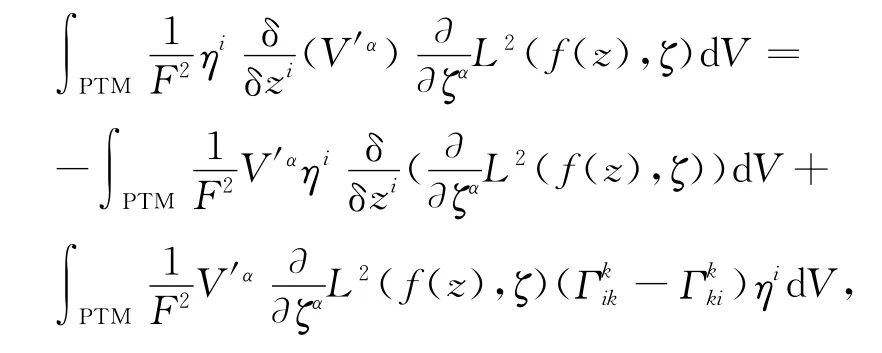
且

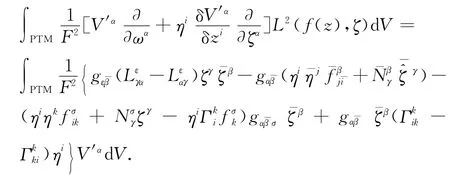
类似地，

以及

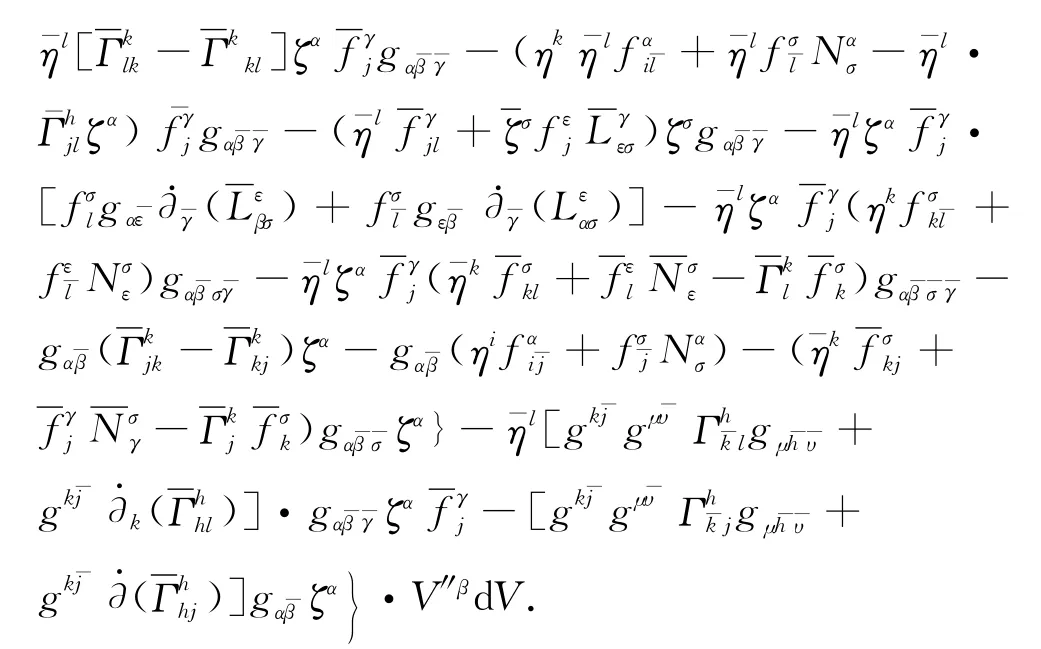
因此，有

定理1 设（M，）为紧强拟凸复Finsler流形，（N，L）为强拟凸复Finsler流形.若f：（M，F）→（N，L）为非退化且非反全纯映射，∂－能量泛函的第一变分为

其中

以及

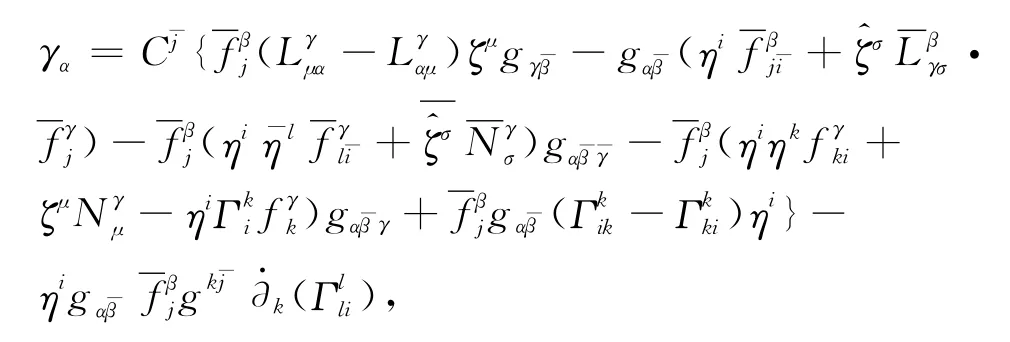
和

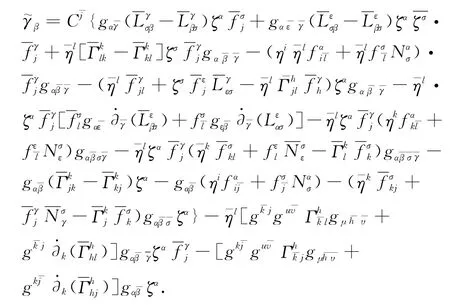
类似地，

定理2 设（M）为紧强拟凸复Finsler流形，（N，L）为强拟凸复Finsler流形.若f：（M，F）→（N，L）为非退化且非全纯映射.则－能量泛函的第一变分为

其中：

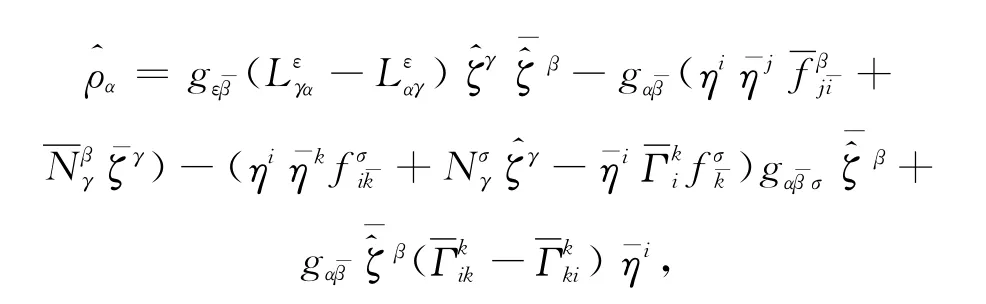
以及

和

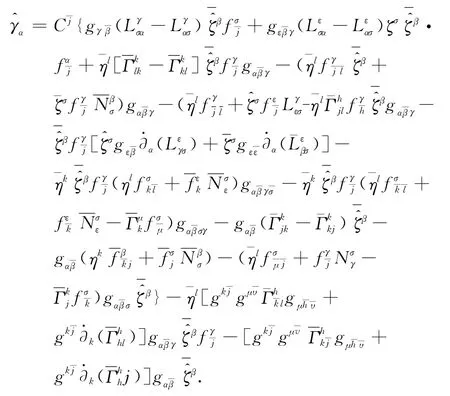
注意1 若（N，L）为Hermite流形同样可以得到文献 [7]中的定理3.1.

注意2 若（M，F）为紧Riemann曲面，可以得到文献[6]中的结果.

令

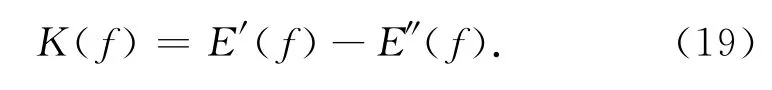
则，

定理2 在复Finsler流形上，K（f）不是同伦不变的.

由式（17）和（18）知，对于 Käahler流形间的光滑映射f，K（f）是同伦不变的.

[1] He Q，Shen Y B.Some results on harmonic maps for Finsler manifolds[J].International Journal of Mathematics，2005（16）：1017.

[2] He Q，Shen Y B.Some properties of harmonic maps for Finsler manifolds[J].Houston Journal of Mathematics，2007（33）：683.

[3] Mo X H.Harmonic maps from Finsler manifolds[J].Illinois Journal of Mathematics，2001，45（4）：1331.

[4] Mo X H，Yang Y.The existence of harmonic maps from Finsler manifolds to Riemannian manifolds[J].Science in China Series A：Mathematics，2005，48（1）：115.

[5] Shen Y B，Zhang Y.Second variation of harmonic maps between Finsler manifolds[J].Science in China Series A：Mathematics，2004，47（1）：39.

[6] Nishikawa S.Harmonic maps of Finsler manifolds[C]∥Topics in Differential Geometry. Bucharest： Editura Academidi Române，2008：207－247.

[7] Han J W，Shen Y B.Harmonic maps from complex Finsler manifolds[J].Pacific Journal of Mathematics，2008，236（2）：341.

[8] Jost J，Yau S T.A nonlinear elliptic system for maps from Hermitian to Riemannian manifolds and rigidity theorems in Hermitian geometry[J].Acta Mathematica，1993，170（2）：221.

[9] Munteanu G.Complex spaces in Finsler，Lagrange and Hamilton geometries [M]. [S.l.]：Kluwer Academic Publishers，2004.

[10] Xiao J X，Zhong T D，Qiu C H.Bochner technique in Strongly Kähler Finsler manifolds[J].Acta Mathematica Scientia，2010，30（B1）：89.

[11] Bland J，Kalka M.Variations of holomorphic curvature for Kähler Finsler metrics[J].Contemporary Mathematics，1996（196）：121.