面向浮动车取样偏差修正的数据融合方法

李慧兵，杨晓光

（同济大学 交通运输工程学院，上海 201804）

路段平均行程时间作为反映道路拥挤程度的关键交通参数之一，历来受到交通管理与控制部门的高度重视.路段平均行程时间的精确度、完整性与时效性，直接影响动态交通管理措施的应用效果.

不同数据源需要不同的模型算法来估计和预测路段平均行程时间值，考虑在我国大中城市路网上，浮动车数据具有数据精度高，覆盖范围广，成本低等优点，因此，对路段平均行程时间的估计和预测来说，目前浮动车数据应用最广［1］.然而由于浮动车样本量的限制［2］，以及浮动车参数计算模型的局限性［3］，单纯利用浮动车数据计算得到的路段平均行程时间（average link travel time，ALTT）的精度常常无法满足先进交通管理系统（advanced traffic management system，ATMS）系统的需求.

前人的研究表明：浮动车样本的路段平均行程时间可以准确地反映穿越路段全体车辆的路段平均行程时间［4－6］.然而Sen等［7－8］分析了从实地采集到的浮动车数据，在对浮动车路段平均行程时间进行统计分析之后，得到这样的结论：由于浮动车样本的时空分布具有随机性，因此，样本采样总是有偏差的，所以无论浮动车样本量有多大，浮动车样本的路段平均行程时间都可能不会接近全体车辆的路段平均行程时间.Hellinga等［9］近期的文章给出了与Van Aerde等［4］和 Sen等［7］不同的结论，但 Van Aerde等［4］和Sen等［7］的结论本身并没有错误，它们都只是适用于特定交通和浮动车样本量情况.这些文章［7－9］均表明：由于浮动车样本的偏差，不管浮动车数据的样本量有多大，单纯利用浮动车数据计算出来的路段平均行程时间都可能无法逼近全体车辆的路段平均行程时间.

在参考传统浮动车模型和真实路段平均行程时间模型的基础上，本文提出一种基于浮动车数据和线圈数据的数据融合模型，然后对模型提出的小时段进行划分，最后对模型进行实例验证.

1 融合数据环境

为了把上述融合模型应用于实际中，路网中的线圈应该采用实时自适应交通控制系统的线圈布设方式，这些线圈可以检测到每1s内交叉口上游出口的断面流量、占有率等数据；运行在路网上的浮动车实时发送（数据采样间隔为1s）浮动车数据，该数据包括车辆经纬度、时间、点速度、车辆编号等.由于浮动车每1s发送一次数据，通过比对每辆浮动车的实时经纬度与检测线圈的位置，就可以得到每辆浮动车通过线圈检测器的具体时刻.

2 融合模型建立

本融合模型是基于以下假设建立起来的：在某小时段内到达的每辆浮动车的运行轨迹（路段行程时间）同与该浮动车在同一小时段内到达的其他车辆的运行轨迹（路段行程时间）相似.

2.1 传统浮动车模型

基于浮动车数据的路段平均行程时间传统模型如下：

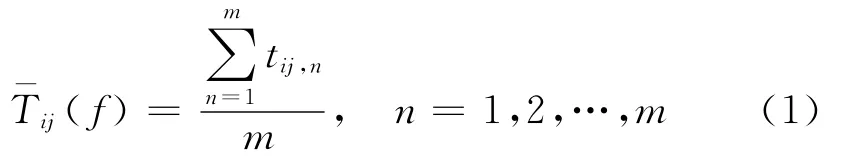
由于传统模型未考虑浮动车取样偏差对路段平均行程时间计算的影响，因此单纯利用浮动车数据计算得到的路段平均行程时间存在较大误差.

2.2 真实路段平均行程时间模型

假设路段平均行程时间的计算间隔为5min（全文同），那么路段上全体车辆的路段平均行程时间（路段平均行程时间真实值）可表示如下：

2.3 融合模型

参照式（2），把其中小时段内真实平均行程时间替换为单辆浮动车的行程时间，即可得到本文的融合模型.该模型可有效融合线圈流量数据和浮动车行程时间，其表达式如下：

其中，根据每个计算间隔内通过某路段的浮动车数m，把该间隔划分为m个小时段，每辆浮动车都会在其对应的小时段内通过目标路段，比如，第1辆浮动车会在第1个小时段通过目标路段，第2辆浮动车会在第2个小时段通过目标路段，…，第m辆浮动车会在第m个小时段通过目标路段.对比公式（2）和（3），可以看出，要使式（3）的融合结果接近于式（2）的真实路段平均行程时间，就必须使tij，n接近.Hellinga等［9］指出，在浮动车行程时间计算间隔内，不同时刻到达的浮动车会产生不同的延误，比如，在有效红灯间隔内到达交叉口进口道的浮动车与在有效绿灯间隔内到达进口道的浮动车所产生的延误差别很大，甚至在同一有效红灯间隔内，不同时间点到达的浮动车所产生的延误也会有较大差别（在过饱和交通状态下，很多车辆会经历二次排队，这些车辆所产生的延误要比只经历过一次排队的车辆要大得多）.为了使tij，n接近，如何划分计算间隔i内的m个小时段就显得尤为重要.

3 小时段划分方法

某计算间隔（5min）内小时段划分的原则在于——使每个小时段内通过的浮动车行程时间tij，n接近于该小时段内通过的全体车辆路段平均行程时间.如果tij，n与该小时段内其余车辆的行程时间相接近，那么tij，n就比较接近了.

为了清晰地表述小时段的划分方法，需要设定一条示例路段（图1），该路段为1号交叉口与2号交叉口之间，西向东的左转路段.

融合2号线圈检测器组检测到的流量数据以及每辆浮动车的行驶轨迹信息（图2），可以对计算间隔i的小时段进行划分.

小时段划分流程如下：

（1）记录在计算间隔i（5min）内，通过示例路段所有浮动车的ID号以及浮动车数；

图1 示例路段示意图Fig.1 Diagram of object link

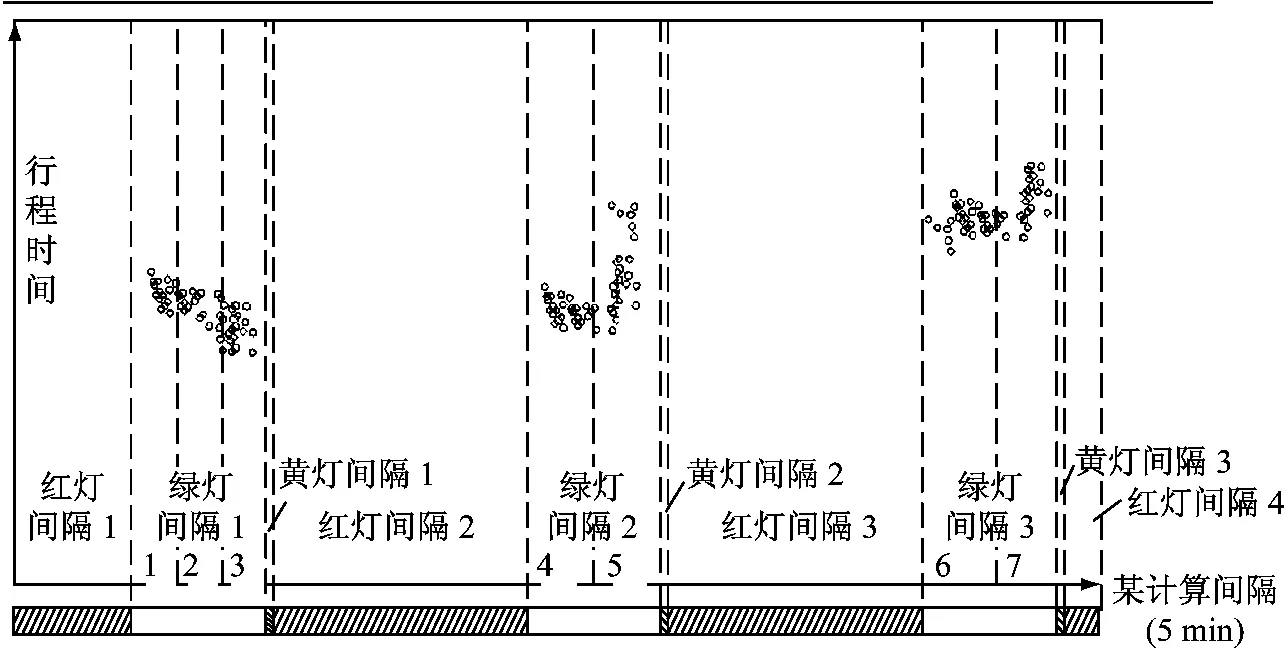
图2 2号线圈检测器组检测到的流量以及浮动车分布图Fig.2 Distribution of traffic flow and floating cars detected by the 2nd loop detectors

（2）记录每辆浮动车分别通过交叉口出口断面线圈检测器组1和2的时刻，它们之间的时间差就是该浮动车穿越示例路段的行程时间；

（3）利用式（1）计算得到基于浮动车数据的路段平均行程时间；

（4）如图2所示，横坐标代表某计算间隔的长度（5min），纵坐标代表行程时间，坐标下方给出了2号交叉口左转相位在该5min内的信号配时图.从该图2可以看出，有7辆浮动车在该时间间隔内通过示例路段.

（5）小时段划分的前提是：每一小时段内均有一辆浮动车通过示例路段.由于在红灯间隔内，不会有车辆通过，因此，不考虑红灯间隔，只考虑3个绿灯＋黄灯的间隔.在每个（绿灯＋黄灯）间隔内，假设有k（k≥2）辆浮动车通过，则第1辆浮动车所属小时段始于该计算间隔i的起点，终于第1辆和第2辆浮动车分别到达2号检测器组的时间中点，第k辆浮动车所属小时段始于第（k－1）辆和第k辆浮动车分别到达2号检测器组的时间中点，终于该（绿灯＋黄灯）间隔的终点.第i（i＝2，3，…，k－1）辆浮动车所属小时段均始于第（i－1）辆和第i辆浮动车分别到达2号检测器组的时间中点，终于第i辆和第（i＋1）辆浮动车分别到达2号检测器组的时间中点.

这种划分方法可以保证行驶轨迹相似（或在2号交叉口处所经历的延误相近）的车辆被划分在同一小时段.同时，计算间隔i内的浮动车样本量越大，利用该融合模型计算得到的路段平均行程时间准确度就会越高，因为此时计算间隔所划分的小时段数变多，某小时段内浮动车样本的行驶轨迹（路行程时间）就会更接近于该小时段内其余车辆的行驶轨迹（路段行程时间）.

4 实例分析

4.1 数据来源

本文以南京市中山路南北向的道路（介于建宁路与汉中路之间）作为实际参照路网，利用Vissim生成该路网上的各种原始数据，包括浮动车数据、线圈数据、各路段的实际行程时间等.如图3所示，仿真路网为一条主干路，包括5个交叉口和4条路段，所有交叉口的信号控制方式都为定时控制，信号配时是典型的4相位配时方案，信号周期均为120s.最后，该路网生成一个平峰和一个晚高峰（10：00～10：45和17：40～18：25）两个时段的数据，其中浮动车占全体车辆的百分比介于1%和10%之间.本文的研究对象为路段1左转相位所在的路段（介于广州路与汉中路之间，长度为400m），研究的目标变量是该路段的平均行程时间（图3）.

图3 仿真路网Fig.3 Road network based on Vissim simulation

4.2 实验结果分析

本文使用相对误差（relative error，RE）和平均相对误差（mean relative error，MRE）来对融合模型的有效性进行评价，表示如下：

式中：REi为第i个计算间隔内的路段行程时间相对误差；Ai为第i个计算间隔下的实际路段行程时间；Ei为第i个计算间隔下的路段行程时间估计值；n为评价时段内的计算间隔数.

根据Vissim获取的路网原始数据，通过传统浮动车模型和融合模型分别计算研究路段的平均行程时间，得到一个平峰和一个晚高峰（10：00～10：45和17：40～18：25两个时段）下的路段平均行程时间，见表1—2；分别计算这两种模型下的行程时间相对误差（表3—4），同时绘制相应的曲线图（图4—7）.其中，基于传统浮动车模型的路段平均行程时间估计值用ATF表示，基于融合模型的路段平均行程时间估计值用ATD表示，路段平均行程时间真实值用RAT表示；基于传统浮动车模型的路段平均行程时间相对误差用REF表示，基于融合模型的路段平均行程时间相对误差用RED表示.

在平峰期，基于传统浮动车模型计算得到的路段平均行程时间MRE为14.75%，基于融合模型计算得到的路段平均行程时间MRE为5.01%.

在高峰期，基于传统浮动车模型计算得到的路段平均行程时间MRE为16.62%，基于融合模型计算得到的路段平均行程时间MRE为7.23%.

表1 在平峰期，不同模型下计算得到的路段平均行程时间Tab.1 ALTTs based on different calculation methods during the off－peak period s

表2 在高峰期，不同模型下计算得到的路段平均行程时间Tab.2 ALTTs based on different calculation methods during the peak period s

表3 在平峰期，不同模型下计算得到的路段平均行程时间相对误差Tab.3 RE of ALTTs based on different calculation methods during the off－peak period %

表4 在高峰期，不同模型下计算得到的路段平均行程时间相对误差Tab.4 RE of ALTTs based on different calculation methods during the peak period %

图4 在平峰期，不同模型下计算得到的路段平均行程时间曲线图Fig.4 Curves of ALTT based on different models during off－peak period

图5 在高峰期，不同模型下计算得到的路段平均行程时间曲线图Fig.5 Curves for ALTT based on different models during peak period

图6 在平峰期，不同模型下计算得到的路段平均行程时间RE曲线图Fig.6 Curves of RE of ALTT based on different models during off－peak period

图7 在高峰期，不同模型下计算得到的路段平均行程时间RE曲线图Fig.7 Curves of RE of ALTT based on different models during peak period

5 结论

（1）本文首先基于传统浮动车模型对路段平均行程时间进行估计，其相对误差较大（平峰期MRE为14.75%；高峰期 MRE为16.62%）；建立了一个融合模型，利用该模型分别在平峰时段和高峰时段对路段平均行程时间进行估计，与传统浮动车模型相比，其行程时间相对误差显著减小（平峰时段MRE为5.01%；高峰时段MRE为7.23%），基本满足出行者对实时信息精度的要求，因此可以作为改进的浮动车计算模型应用于ITS智能交通系统中.

（2）该模型可以很大程度上消除浮动车的取样偏差，因此具有较大的理论价值和实际应用价值；但是出于理论研究的必要性，仿真路网中的交叉口采用的是固定信号配时，实时自适应交通控制系统内的交叉口信号配时实行实时微调，因此该模型在该系统中的实际应用效益还需要进行实地验证［10］.

（3）研究中浮动车数据的采样间隔为1s，但实际中浮动车数据的采样间隔一般为10—30s，因此，需要修正该模型以便将其更好地应用于实践.当浮动车数据发送间隔比较大（10—30s）时，可通过融合交叉口信号配时信息及每个浮动车点的状态信息，结合动态的路段划分，来获取每辆浮动车通过线圈检测器的时刻［11－12］.

（4）目前许多城市采用的不是实时自适应交通控制系统，并且线圈检测器很容易毁坏，因此如何利用该融合模型对浮动车数据和其他类型检测器（视频检测器，雷达检测器等）检测到的车流量进行融合是一个值得研究的课题.

［1］姜桂艳，常安德，吴超腾.基于GPS浮动车的交通信息采集方法［J］.吉林大学学报：工学版，2010，40（4）：971.JIANG Guiyan，CHANG Ande， WU Chaoteng.Traffic information collection method based on GPS equipped floating car［J］.Journal of Jilin University：Engineering and Technology Edition，2010，40（4）：971.

［2］张存保，杨晓光，严新平.基于浮动车的交通信息采集系统研究［J］.交通与计机，2006，24（5）：31.ZHANG Cunbao，YANG Xiaoguang，YAN Xinping.Traffic data collection system based on floating cars［J］.Computer and Communications，2006，24（5）：31.

［3］胡明伟.基于GPS的实时交通信息采集方法的研究［J］.公路交通技，2007，24（5）：121.HU Mingwei.Study on GPS－based real－time traffic information collection method［J］.Journal of Highway and Transportation Research and Development，2007，24（5）：121.

［4］Van Aerde M，Hellinga B，Yu L，et al.Vehicle probes as realtime ATMS sources of dynamic O－D and travel time data：large urban systems［C］／／Proceedings of the ATMS Conference.Petersburg：［s.n.］，1993：207－230.

［5］Srinivasan K K，Jovanis P P.Oversaturation delay estimates with consideration of peaking［C］／／Transportation Research Record 1537，TRB.Washington D C：［s.n.］，1996：15－22.

［6］Turner M S，Holdener D J.Probe vehicle sample sizes for realtime information：the Houston experience［C］／／Proceedings of Vehicle Navigation and Information Systems （VNIS）Conference.Seattle：［s.n.］，1995：3－9.

［7］Sen A，Thakuriah P，Zhu X，et al.Frequency of probe reports and variance of travel time estimates ［J］.Journal of Transportation Engineering，1997，123（4）：285.

［8］Sen A，Soot S，Ligas J，et al.Arterial link travel time estimation：probes，detectors and assignment－type models［C］／／Preprint No.970943，Transportation Research Board，76th Annual Meeting. Washington D C：Transportation Research Board，1997：1256－1272.

［9］Hellinga B，Fu L.Assessing expected accuracy of probe vehicle travel time reports［J］.Journal of Transportation Engineering，American Society of Civil Engineers，1999，125（6）：1.

［10］王明军，李志恒，张毅.基于UTC／SCOOT的城市交通控制管理平台设计应用［J］.公路交通科技，2006，23（6）：37.WANG Mingjun，LI Zhiheng，ZHANG Yi. Design and application of traffic control management platform based on UTC／SCOOT［J］.Journal of Highway and Transportation Research and Development，2006，23（6）：37.

［11］姜桂艳，常安德，张玮.基于GPS浮动车的自然路段行程时间估计方法［J］.公路，2009，2（5）：87.JIANG Guiyan，CHANG Ande，ZHANG Wei.Physical link travel－time estimation method based on GPS equipped floating Car［J］.Highway，2009，2（5）：87.

［12］于德新，高学英，杨兆升.基于GPS数据及车辆运行特性分析的单车路段行时间估计［J］.吉林大学学报：工学版，2010，40（4）：965.YU Dexin，GAO Xueying，YANG Zhaosheng.Individual vehicle travel－time estimation based on GPS data and analysis of vehicle running characteristics［J］.Journal of Jilin University：Engineering and Technology Edition，2010，40（4）：965.