方形高层建筑风压脉动非高斯特性分析

韩 宁，顾 明

（同济大学 土木工程防灾国家重点实验室，上海200092）

在风工程实际应用中通常假设结构表面风压服从正态分布，并据此得到结构的设计风荷载.然而，大量的风洞试验还有现场实测证明结构表面的实际风压并非全部如此.对于高层建筑，在其表面来流的分离区内实测得到的压力脉动就是典型的非高斯分布.如果仍按照高斯分布的假定来计算围护结构表面的风压将会得到偏低的结果，这对围护结构是不安全的.目前，仅有较少的研究涉及高层建筑风压的非高斯特性.Peterka等［1］指出来流直接撞击到结构表面，在迎风面表现为广义正平均风压，其他3个面表现为负的平均风压，而介于两者之间的测点所占据的百分比很小，本文的试验数据也验证了这一结论.但是Peterka等［1］通过上述平均风压来区分高斯和非高斯分布并不总是正确，Lou［2］证实在高层建筑的正压区域也会出现偏度.Kumar［3］在其博士论文中定性地给出偏度大于0.5且峰度大于3.5为高斯和非高斯的界限.但文献［3］的研究对象为低矮建筑物，该结论并不能完全适用于其他形式的结构.譬如孙瑛等［4］在对大跨屋盖结构进行非高斯分析时采用同样的方法得到的标准却是偏度绝对值大于0.2且峰度绝对值大于3.7.本文的研究对象为高层建筑，在用Kumar的结论进行非高斯分析时同样发现其并不适应于这种结构形式，所以，本文在其研究的基础上，独立给出了高层建筑结构非高斯的描述方式，然后分析了单体方形高层建筑非高斯特性，并对其表面进行了分区.

1 试验简介

试验模型为尺寸为900mm×150mm×150 mm的方柱，几何缩尺比为1∶400.在模型上共计布置496个测点，每个立面上均有124个测点，4个面测点布局相同，均在模型的最上部和棱边处布置较密的测点，具体的测点布置图见文献［5］.试验在同济大学土木工程防灾国家重点实验室TJ－2风洞进行.TJ－2风洞为闭口回流式矩形接口风洞，试验段宽3.0m、高2.5m、长15.0m.采用被动模拟方法在TJ－2风洞模拟了我国规范（GB50009—2001）［6］中的C类风场，几何缩尺比为1∶400.由于我国规范未直接给出各类地貌紊流度剖面，故本次试验采用日本建筑荷载规范（AIJ2004）［7］建议的紊流度公式.详细的平均风速剖面和紊流度剖面的模拟结果与理论值的比较见文献［5］.单体方形建筑风向角如图1.

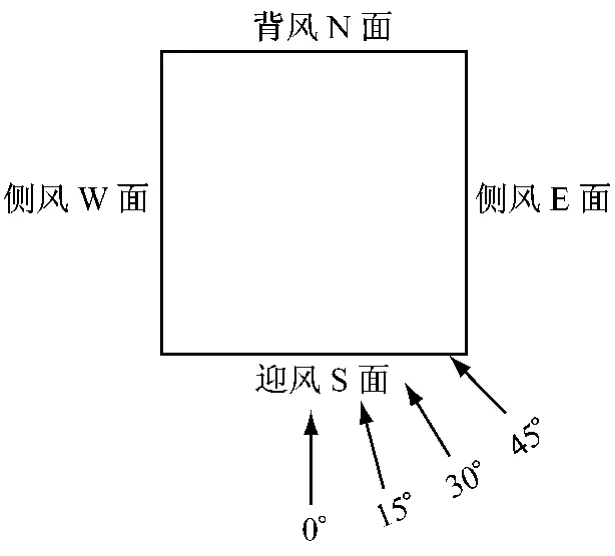
图1 单体方柱风洞试验风向角示意Fig.1 Schematic diagram of wind angle of the single square model

2 非高斯特性描述

偏度（skewness）系数定义如式（1）所示，它是3阶中心矩与均方差的3次方的比值，记为S；峰度（kurtosis）系数定义如式（2）所示，它是4阶中心矩与均方差的4次方的比值，记为K.

服从高斯分布的随机变量的偏度和峰度分别为零和3.偏度体现的是概率分布的非对称性，当偏度大于零时，分布曲线为正偏态曲线，此时曲线的长尾部在横轴正方向，当偏度小于零时，分布曲线为负偏态曲线，此时曲线的长尾部在横轴负方向，见图2a；峰度是用来描述概率分布曲线较高斯分布的凸起程度，当峰度小于3时，分布曲线的峰度比正态曲线低，称为平阔峰曲线，其尾部较高斯分布薄；当峰度大于3时，曲线比较尖峭，称为尖峭峰曲线，其尾部较高斯分布厚，见图2b.综上可知，可以采用偏度和峰度来对信号的非高斯特性进行描述.

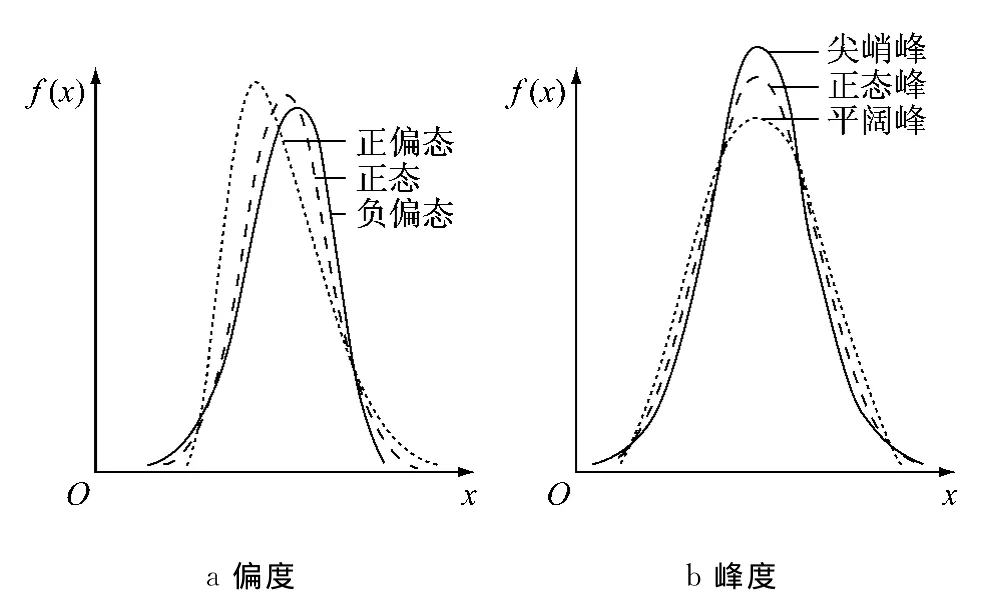
图2 高斯分布和非高斯分布对比Fig.2 Comparison of Gaussian and non－Gaussian distribution

通过对试验结果的处理分析得知0°风向角下迎风面测点风压时程的偏度和峰度间存在一定的关系，如图3.图中 （K－S）／K为归一化峰度.由图可以看出，S面上两者线性相关，但其他3个立面上并不存在这种关系.另根据已有的研究结论，垂直于来流风向的高层建筑其迎风面测点风压分布基本符合高斯分布，这可能意味着其他3个面并不符合高斯分布，这也同时表明非高斯和高斯测点偏度、峰度间的关系并不相同，所以本文正是基于此思想来判断高斯和非高斯的.

对0°风向角下迎风面偏度、归一化峰度（K－S）／K进行回归分析得到如下回归方程：

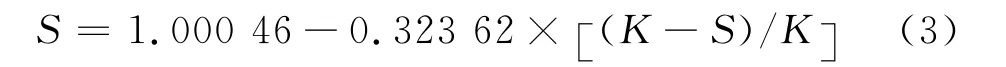
当测点的偏度、峰度满足式（3）时，就认为其服从高斯分布，否则为非高斯分布.在对大量试验数据进行分析后发现该标准有点苛刻，所以本文同时结合各个测点的概率密度图并最终得到高层建筑非高斯特性的判别标准为：｜S｜≥0.25且K≥3.2或｜S｜≥0.45或K≥4.0，其中最后2个条件是考虑偏度、峰度间并不呈线性增加的关系，譬如会出现偏度很大、峰度很小，或是偏度很小、峰度很大的情况，如图4.文献［3］中没有考虑这种情况，本文为了更全面地考虑非高斯测点故将这2种特殊情况亦考虑其中，也即由于偏度很大引起的非高斯和由于峰度很大引起的非高斯2种情况.

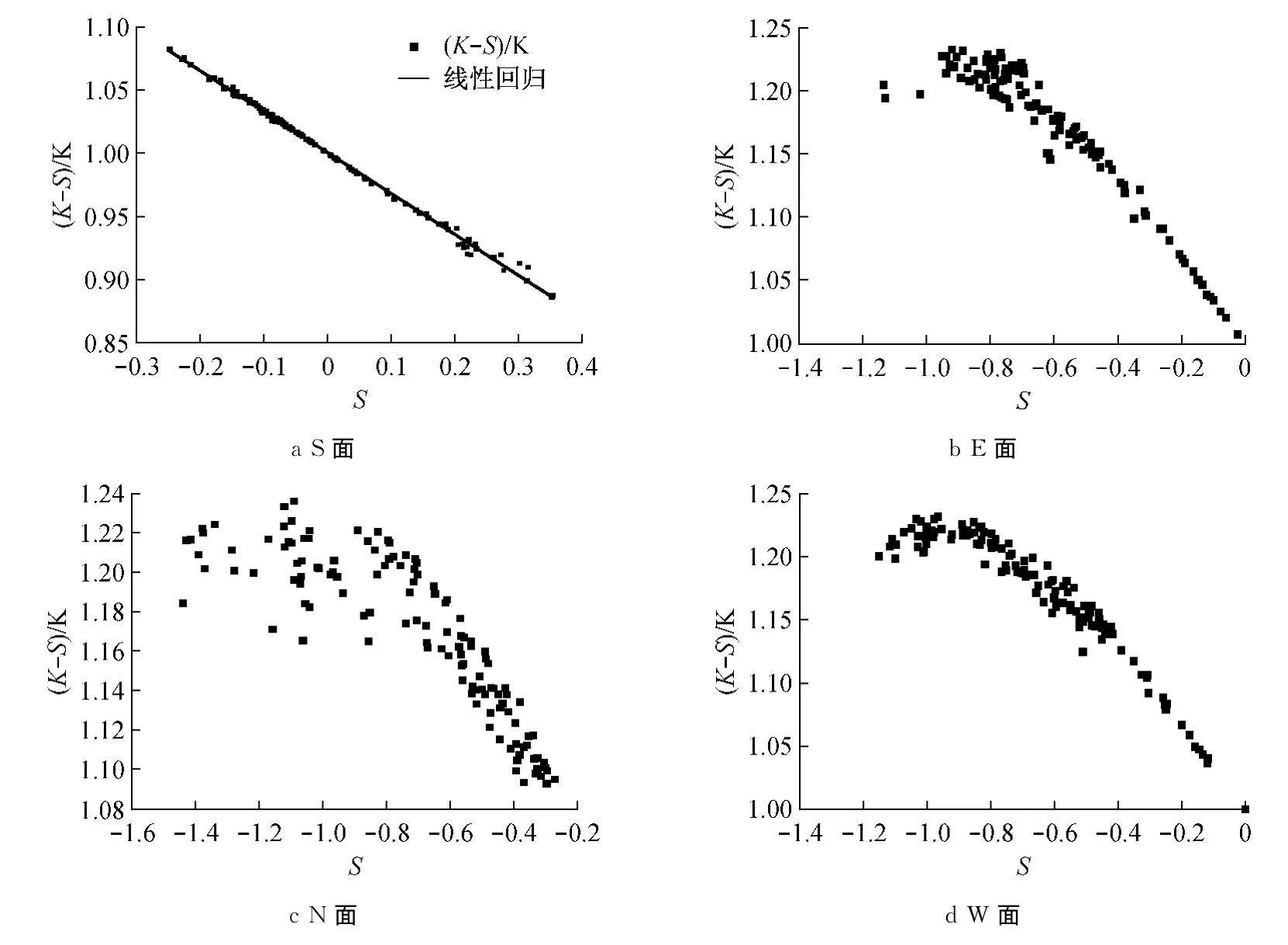
图3 单体建筑0°风向角下偏度和归一化峰度间关系Fig.3 The relationship of skewness and normalized kurtosis on isolated building at 0°wind angle

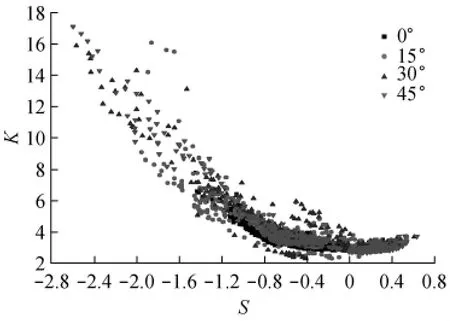
图4 单体建筑给定风向角下4个面偏度、峰度关系Fig.4 The relationship of skewness and kurtosis on isolated building at given wind angles

3 结果分析

由于是方形建筑，截面对称分布，所以这里仅给出4个风向角的影响.

图5为方柱各立面偏度等值线随风向角变化分布图，其中Smax，Smin分别为偏度极大和极小值.由图5a可见，4个风向角下S面均同时出现正偏和负偏，其中正偏占据了S面的大部分区域且正偏值大于0.25的区域随风向角的增大而自S面中部向上扩大.负偏区域在0°风向角下最大，其随风向角增大主要分布在来流风向的左侧靠近棱边区域.单点负偏绝对值在45°风向角下取得最大值1.00，说明此时来流左侧棱边处由于分离流产生的负压较大.图5b中E面偏度等值线随风向角的变化较为显著.在0°风向角下偏度均为负值而在其他风向角下偏度出现了正值，这是因为当风向角增大时，E面部分区域会直接受到来流风的作用.负偏绝对值大于0.45的区域随风向角的增大而减小且位置发生变化.N立面的偏度值在给定的4个风向角下均为负值，如图5c中所示，负偏绝对值大于0.45的区域在风向角由0°增大到30°时逐渐减小，但在45°风向角下又显著增大，这是因为当风向角增大到特定角度之前，N面受其两侧棱边分离流的影响基本相同，而超过该临界角度时，其中一侧棱边的分离流就会占据主要地位.N面单点负偏绝对值在45°风向角下取得最大值2.50，位于远离来流一侧棱边的0.30H（H为建筑高度）处，这或许是由柱状涡旋引起的.由图5d可以看出，W面偏度值在给定风向角下均为负值.负偏绝对值大于0.45的区域随风向角的增大而扩大，当风向角大于0°时，单点负偏绝对值的极大值主要位于远离来流一侧棱边的0.50H附近，其在45°风向角下取得最大值2.70.

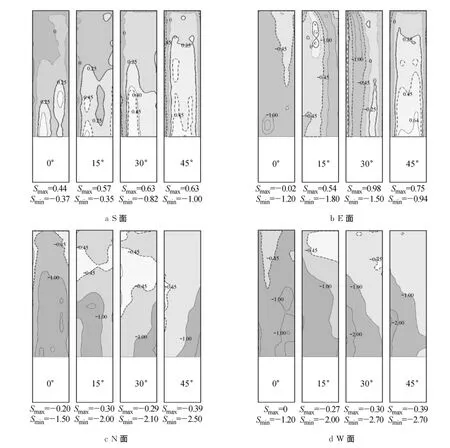
图5 方形建筑各立面偏度等值线随风向角变化分布Fig.5 Contours of skewness on the square building at various wind angles

图6 为方柱各立面峰度等值线随风向角变化分布图，其中Kmax，Kmin分别为峰度极大和极小值.由图6a可以看出，S面峰度值相较于其他3个立面偏小，其峰度大于4.0的区域在0°风向角下主要位于0.40H和0.55H之间远离棱边的中间区域，而在其他风向角下则位于两侧棱边处，因为风向角增大改变了整个立面的流场，使得在0°风向角下立面中部形成的涡旋被打乱而棱边处的分离流却增强了.和偏度等值线分布图不同的是，单点峰度值在30°风向角下取得最大值5.4，这表明偏度和峰度值并不总是同步增大的.由图6b看出风向角对E面峰度的影响较为显著.峰度值小于3.2的区域在15°时位于E面的中间狭长区域而在30°时则移动到靠近棱边的两侧区域，在45°风向角下占据了E面的绝大部分区域，这表明该风向角下峰度偏离正态峰的程度最小.单点峰度值在15°风向角下取得最大值9.4，位于靠近后侧棱边0.60H处.N面峰度等值线随风向角的变化相对较为规则，如图6c所示，峰度大于4.0的区域随风向角的增大呈减小趋势且逐渐向远离来流一侧移动，这是因为N面在0°风向角下受尾流的影响最大，而随着风向角的增大，分离流开始起作用，这样在分离流和尾流综合作用下单点峰度最大值出现在45°风向角下，数值为17.0，位于远离来流侧的0.30H处.由图6d可见，W面峰度等值线分布图在0°风向角下和其他3个风向角有显著不同，在0°风向角下，其前侧为分离流区域，所以峰度值大于4.0的区域主要位于此，但在其他3个风向角下，峰度值大于4.0的区域则分布于沿着约50°角斜向下的后侧区域，这或许是因为当风向角增大时W面逐渐处于尾流和分离流的综合作用下.单点峰度在45°风向角时取得最大值18.0，位于靠近左棱边0.45H附近.

图6 方形建筑各立面峰度等值线随风向角变化分布Fig.6 Contours of kurtosis on the square building at various wind angles

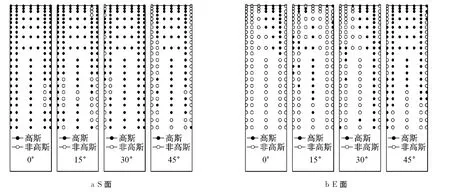
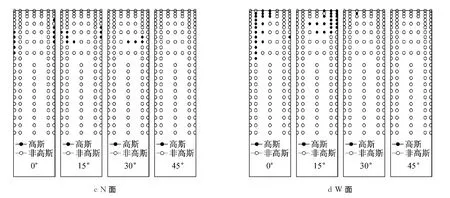
图7 单体建筑各个立面非高斯区域随风向角变化分布Fig.7 Non－Gaussian zones on each face of isolated building at various wind angles

由图7可以看出，① 对于S面，高斯区域占据S面绝大部分区域，这是因为在给定的风向角范围内S面均受来流直接作用.非高斯区域随风向角的增大而增大，所以45°风向角为最不利风向角.② 在0°风向角下可以清晰看出E面分离区和再附区的位置，在0.90H以上的迎风棱边角部和0.80H以下呈斜向下一个弧度为分离流区域，这和文献［8］的结论是一致的.随着风向角的增大逐渐有部分来流直接作用到E面上，原来的分离区和再附区被打乱，此时非高斯区域主要位于E面前缘或是后缘部分.当风向角为45°时，来流处于主导控制地位，高斯区域此时分布面积最大，非高斯区域主要位于0.40H以下，这或许是由于此处形成了柱状涡造成的.③ 给定风向角范围内N面基本为非高斯区域，高斯区域仅出现在风向角介于0°和30°之间时S面0.80H的局部很小区域.④给定风向角范围内W面以非高斯区域为主，高斯区域仅出现在风向角介于0°和15°之间时W立面0.80H以上的左侧或是右侧区域.

4 结论

（1）通过对测点风压时程的偏度、峰度及概率密度函数图进行归纳分析，给出了高层建筑非高斯特性的判断准则.

（2）分析了高层建筑非高斯特性随风向角变化的趋势并给出了不同风向角下高斯和非高斯分区，发现受来流直接作用的立面主要为高斯区域而受分离流和尾流作用的区域主要为非高斯区域.对于规则高层建筑物可以根据给出的非高斯区域分布图推测不同风向角下其大致分布情况.

（3）实际工程中可以找出建筑的主导风向角从而给出建筑物围护结构非高斯区域，再进一步进行极值分析.

［1］Peterka J A，Cermak J E.Wind pressures on buildings—probability densities［J］.Journal of Structual Division，1975，101（6）：1255.

［2］Lou J J.Extreme value analysis of peak wind pressure on buildings［D］.Fort Collins：Colorado State University，1981.

［3］Suresh Kumar，K.Simulation of fluctuating wind pressures on low building roofs［D］.Montreal：Concordia University，1997.

［4］孙瑛，武岳，林志兴，等.大跨屋盖结构风压脉动的非高斯特性［J］.土木工程学报，2007，40（4）：1.SUN Ying，WU Yue，LIN Zhixing，et al.Non－Gaussian features of fluctuating wind pressures on long span roofs［J］.China Civil Engineering Journal，2007，40（4）：1.

［5］韩宁，顾明.两串列方柱局部脉动风压干扰研究：第1部分 迎风面效应［J］.振动与冲击，2009，28（12），188.HAN Ning，GU Ming.Interference effects on local fluctuating pressure of two square tall buildings in tandem arrangement：part 1 windward side effects ［J］.Journal of Vibration and Shock，2009，28（12）：188.

［6］中华人民共和国住房和城乡建设部.GB50009—2001建筑结构荷载规范［S］.北京：中国建筑工业出版社，2006.GB50009—2001 Load code for the design of building structures［S］.Beijing：China Architecture and Building Press，2006.

［7］Architectural Institute of Japan.Recommendations for loads on buildings［S］.Tokyo：Architectural Insitute of Japan，2004.

［8］Peterka J A，Meroney R N，Kothari K M.Wind flow patterns about buildings［J］.Journal of Wind Engineering and Industrial Aerodynamic，1985，21：21.