随机场的随机谐和函数表达
2012-07-31梁诗雪孙伟玲
梁诗雪,孙伟玲,李 杰,2
(1.同济大学 土木工程学院,上海200092;2.同济大学 土木工程防灾国家重点实验室,上海200092)
实际的工程结构,由于材料特性、边界条件和系统输入均不同程度存在随机性,因而在许多场合将工程结构视为随机结构系统[1]是较确定性结构系统较为合理的一种反映方式.举例言之,对于混凝土材料,由于初始随机元(微裂缝、微孔洞等)和随机组分(骨料分布等)的存在,导致工程结构中混凝土强度、弹性模量等是三维随机场.采用概率论的观点才能更科学、细致地反映随机结构的受力力学行为[2].
在随机场直接模拟方法中,最为典型的即为谱表现[3]方 法、Karhunen-Loeve分 解 方 法[4]、双 重 正交分解方法[5]等.文献[6]对有代表性的方法进行了比较研究.然而,由于上述方法采用无穷级数,为了保证足够的精度,须引入足够多的随机变量对随机场进行模拟,增加了计算难度、降低了计算效率.
1969年,Goto和Toki率先提出了一类频率和相位同时具有随机性的谱表现方法[7].Shinozuka等对谱表现方法进行了系统深入的研究[8],并在1996年将这一工作扩展至多维随机场模拟[9].在上述背景下,陈建兵、李杰提出了随机谐和函数的概念[10].在此基础上,孙伟玲等进一步提出了随机过程的第二类随机谐和函数表达[11].研究表明:当频率与相位在经过剖分的子空间内分别服从独立均匀分布、幅值由随机频率与目标功率谱密度决定时,无论随机谐和函数分量的个数是多少,该随机过程的功率谱密度函数均精确地等于目标功率谱密度函数.
本文试图将上述随机谐和函数表达进一步扩展至空间多维随机场,并证实采用随机谐和函数表达二维(多维)随机场的适用性.
1 二维随机场的第二类随机谐和函数表达
随机场是随机过程在空间域(场域)上的自然推广.对于二维随机场f(u)其自相关函数
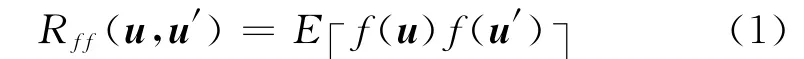
式中:u为二维空间变量,表示数学期望.定义自协方差函数

则自协方差函数与自相关函数关系为Kff(u,u′)=Rff(u,u′)-E(f(u))E(f(u′)).对于平稳随机场,其自相关函数可写为Rff(u,u′)=Rff(u-u′)=Rff(r),r为距离向量.
单个波动组分在时间上的频度称为频率,而在空间上的频度称为波数,其表示2π单位长度内波的个数.波数K=2π/τ,τ为波长.
平稳随机场f(x1,x2)的自相关函数与功率谱密度函数Sff(K1,K2)间存在如下维纳-辛钦关系:
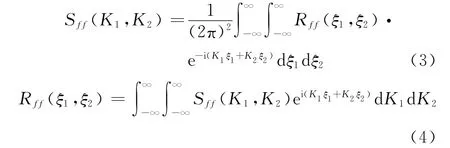
式中:K1,K2分别为x1,x2方向的波数;ξ1,ξ2分别为x1,x2方向的距离.出于实际应用考虑,通常取波数-K1u≤K1≤K1u,-K2u≤K2≤K2u,其中K1u<∞,K2u<∞分别为随机场在x1,x2方向的上限截止波数,由此,式(4)可写为

二维随机场双象限单边功率谱Gff(K1,K2)为

对随机过程的随机谐和函数表达[11]作二维扩展,有二维随机场的随机谐和函数表达

式中:N1,N2为随机谐和函数展开项数;K1n1,K2n2分别为随机场第n1,n2个谐和分量波数;An1n2,分别为幅值和相位角。的内点,且满足的内点,且满足并记波数K1n1,K2n2和相位角为随机变量.
显然,式 (7)的自相 关 函 数 为R~f~f(ξ1,ξ2)=对于式(7)所示的随机谐和函数,存在以下定理:
(2)K1n1,K2n2,n1=1,2,…,N1,n2=1,2,…,N2为相互独立的随机变量,分别服从区间内均匀分布,概率密度函数为pKjnj(Kj).


不妨设f(x1,x2)为零均值的平稳随机场,则应有
证明 由式(7),有
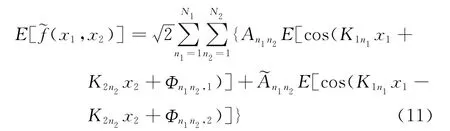
若相位角Φn1n2,1,Φn1n2,2和波数K1n1,K2n2服从均匀分布,易知

将式(14)进行分解


当m1≠n1或m2≠n2时,式(15)第1项可写为

同理,当m1≠n1或m2≠n2时,式(15)第4项的值也为零.考察式(15)第2,3项,对于任意m1,m2,n1,n2易知其值恒为零.综上所述,仅考虑第1项和第4项在m1=n1且m2=n2时有

将式(8)~(10)代入(17),有

2 随机谐和函数随机场的性质
2.1 平稳性
由第1节的证明同时根据式(18)可见采用随机谐和函数表达的随机场的相关函数仅与坐标差有关,且(x1,x2)为零均值平稳随机场.
2.2 渐进正态性
采用Laning-Batting提出的双变量中心极限定理[12]并推广到空间域,则满足定理(1)的条件且当N1,N2→∞时,随机场(x1,x2)任意n个坐标点的截口随机变量组成的随机向量((x11,x21),(x12,x22),…,(x1n,x2n))趋向于多维联合正态分布.事实上,对于式(7)定义的二维随机场,定义

令Z11,Z21,…,ZN1N2是N1×N2个独立双变量随机向量其1阶矩存在且已知,则此二维随机向量的和为由 Laning-Batting 定理知,当N1→∞且N2→∞时,若满足

考察式(21)括号内第1项,根据孙伟玲等的研究[11]易知:当N1,N2→∞,ΔK1n1→0,ΔK2n2→0时有

类似地,式(21)括号内第2~4项分别为零,因此


根据Laning-Batting定理可知Zn1n2=(Xn1n2,Yn1n2)具有渐进正态性.
根据多维正态随机变量的性质可将结论推广至任意n个坐标值所形成的随机向量,即(~f(x11,x21),(x12,x22),…,(x1n,x2n))均具有渐进正态性.
2.3 截口概率密度函数
通过截口随机变量的概率密度函数考察随机谐和函数式(7)的性质.首先,引入随机谐和函数的前几阶中心距对生成的随机场进行描述,α1~α4分别表示随机场前4阶矩.

同理可证
对随机场4阶中心矩进行讨论,显然峰度系数ce为

将式(6),(9),(10)代入上式,当波数区间ΔK1,ΔK2取ΔK11=ΔK12=…=ΔK1N1=ΔK1=K1u/N1且ΔK21=ΔK22=…=ΔK2N1=ΔK2=K2u/N2时,有


则ce可写为ce=-3γ·(2N1N2)-1.
对于随机场的一维概率密度函数,当前4阶矩均已知时,可以采用Pearson[13]分布函数族逼近pf(y,(x1,x2))的表达式

前已述及二维随机谐和函数形式前4阶矩不随坐标位置的变化而改变,因此p~f(y,(x1,x2))=由此可以获得随机场的一维概率密度函数.
采用相对熵[14]比较2个概率密度函数的近似程度:若2个函数完全相同,则相应的相对熵为零.2个函数相差越大,则相对熵绝对值越大.取标准正态分布为目标分布,相对熵φ)表示如下:

此时,考察p~f(y)趋向于正态分布的速率,对σ2=1的情况进行讨论[11],由Pearson分布形式和归一化条件,得

将上式代入式(32)可获得相对熵.图1给出了当二维随机场谱密度形状参数γ取1.5和1.9时随机分量不同取值所对应的截口概率密度分布函数与标准正态分布的概率密度函数,图2给出了相对熵的对比.可见,随着N1,N2的增大,随机场的一维概率密度函数pf(y)很快趋向于标准正态分布,而其相对熵则很快地趋近于零.
3 多维随机场的随机谐和函数表述
式(7)所示的二维随机谐和函数形式可以推广至多维情况.对于m维情况,若目标函数f(u)服从且为平稳随机场,则有


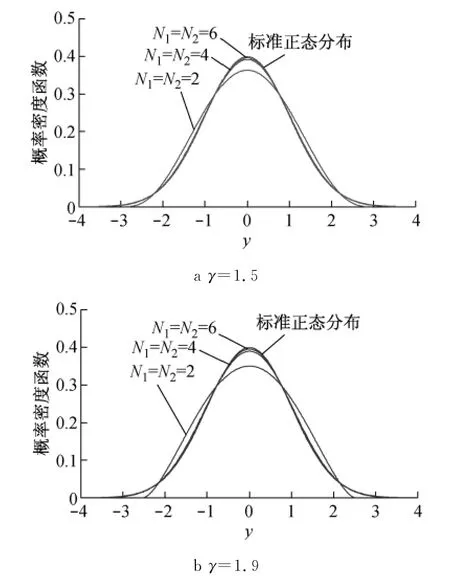
图1 一维概率分布与标准正态分布Fig.1 One-dimensional probability density function and normal distribution

图2 一维概率分布与标准正态分布的相对熵Fig.2 Relatively entrophy of one-dimensional probability density function and normal distribution

4 数值算例
采用式(7)表述的随机谐和函数生成二维随机场.图3a给出了上述情况下目标功率谱密度函数;图3b给出了采用随机谐和分量N1×N2=8×8的目标函数的功率谱密度函数;图3c给出了采用经典谱表现方法×=64×64的功率谱密度函数;图4,图5分别给出了在K1,K2方向的3种功率谱的比较.可见,经典谱表现方法和随机协和函数表达均能较好地符合目标功率谱,然而,采用随机谐和函数生成的随机场所需随机变量更少,计算耗时更短.
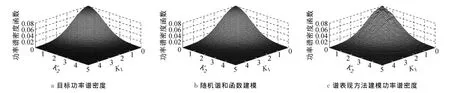
图3 功率谱密度函数Fig.3 Power spectral density function

图4 K1方向功率谱密度函数Fig.4 Power spectral density function spectrum of K1

图5 K2方向功率谱密度函数Fig.5 Power spectral density function spectrum of K2
5 结论
将第二类随机谐和函数推广至多维随机场,可以采用较少的随机谐和分量表示较为丰富的概率信息.证明了对于二维甚至多维随机场,当随机波数和随机相位服从独立均匀分布时,采用有限项随机协和函数表达的随机场的功率谱密度函数可精确地等于目标功率谱函数.同时,这类随机场服从平稳性、渐进正态性.以数值算例验证了采用随机谐和函数生成的二维随机场,相比经典的谱表现方法,本文建议方法可以反映更多的概率信息,所需展开项数更少,计算更为快速、有效.
[1]李杰.随机结构系统——分析与建模[M].北京:科学出版社,1996.LI Jie.Stochastic structural systems:analysis and modeling[M].Beijing:Science Press,1996.
[2]李杰.混凝土随机损伤力学的初步研究[J].同济大学学报:自然科学版,2004,32(10):1270.LI Jie.Research on the stochastic damage mechanics for concrete material and structures [J].Journal of Tongji University:Natural Science,2004,32(10):1270.
[3]Shinozuka M,Jan C M.Digital simulation of random processes and its applications[J].Journal of Sound and Vibration,1972,25(1):111.
[4]Huang S P,Quek S T,Phoon K K.Convergence study of the truncated Karhunen-Loeve expansion for simulation of stochastic processes[J].International Journal for Numerical Methods in Engineering,2001,52(9):1029.
[5]李杰,刘章军.基于标准正交基的随机过程展开法[J].同济大学学报:自然科学版,2006,34(10):1279.LI Jie,LIU Zhangjun.Expansion method of stochastic processes based on normalized orthogonal bases[J].Journal of Tongji University:Natural Science,2006,34(10):1279.
[6]Grigoriu M.Evaluation of Karhunen-Loeve,spectral,and sampling representations for stochastic processes[J].Journal of Engineering Mechanics,2006,132(2):179.
[7]Goto H,Toki K.Structural response to nonstationary random excitation[C]//World of Earthquake Conference Engineering,4th.Santiago:[s.n.],1969:130-144.
[8]Shinozuka M,Deodatis G.Simulation of stochastic processes by spectral representation [J].Applied Mechanics Reviews,1991,44(4):191.
[9]Shinozuka M,Deodatis G.Simulation of multi-dimensional Gaussian stochastic fields by spectral representation[J].Applied Mechanics Reviews,1996,49(1):29.
[10]陈建兵,李杰.随机过程的随机谐和函数表达[J].力学学报,2011,43(3):503.CHEN Jianbing,LI Jie.Stochastic harmonic function and spectral representations[J].Chinese Journal of Theoretical and Applied Mechanics,2010,43(3):503.
[11]孙伟玲,陈建兵,李杰.随机过程的第二类随机谐和函数表达[J].同济大学学报:自然科学版,2011,39(10):1413.SUN Weiling,CHEN Jianbing,LI Jie.Stochastic harmonic functions of the second kind for spectral representations[J].Journal of Tongji University:Natural Science,2011,39(10):1413.
[12]Laning J H,Battin R H.Random processes in automatic control[M].New York:McGraw-Hill,1956.
[13]Zhao Y G,Ono T.Moment methods for structural reliability[J].Structural Safety,2001,23(1):47.
[14]克莱因 M.古今数学思想[M].朱学贤,申又枨,叶其孝,等.上海:上海科技出版社,2002.Kline M.Mathematical thought from ancient to modern times[M].Translated by ZHU Xuexian,SHEN Youcheng,YE Qixiao,et al.Shanghai:Shanghai Science and Technical Publishers,2002.
[15]Shinozuka M,Deodatis G.Response variability of stochastic finite element systems[J].Journal of Engineering Mechanics,ASCE,1988,114(3):499.
