土方调配经济方案的Matlab实现

王 升

(长治市人民防空办公室，山西长治 046000)

1 概述

“三通一平”是施工准备工作的一项重要内容，而场地平整的关键是土方调配方案的确定。土方调配优化方案的确定就是在满足土方总运输量(m3－m)最小或土方总运输成本(元)最小的条件下，确定挖方区和填方区之间土方的调配方向和数量，从而达到缩短工期和降低工程成本的目的。

土方调配最优方案的确定是以线性规划为理论基础，由于土方调配在线性规划中属于运输问题，通常采用单纯形法或表上作业法[1-4]求解，由于表上作业法求解线性规划问题简单方便，应用较为广泛，但由于在用表上作业法确定土方调配时，可能会遇到很多问题，尤其是用“闭回路法”对非最优方案进行调整时，往往要经过多次调整才能找到最优方案，而且所找到的方案只是近似最优解，和精确解之间存在一定的误差。Matlab软件[5]包具有最优化工具箱，可以求解各类优化问题，尤其对线性规划问题的求解，利用Matlab的最优化工具箱可以方便实现。Matlab软件包是当今国际认可的最好的科学计算工具，故文中采用最优化方法进行土方调配方案的求解，并用Matlab编制了相应的计算程序，可供工程技术人员参考使用。

2 土方调配问题数学模型的建立

假设某施工场地有m个挖方区，用i=1，2，3，…，m表示，有n个填方区，用j=1，2，3，…，n表示，已知这m个挖方区的挖方量为a1，a2，a3，…，am，通写为 ai(i=1，…，m)，n 个填方区的填方量分别为 b1，b2，b3，…，bn，通写为 bj(j=1，…，n)，从第 i个挖方区到第j个填方区的土方单位运价或土方平均运距为Cij。上面这些数据通常用单位运价(或平均运距)及填挖土方量平衡表表示，见表1。

假设xij代表从第i个挖方区调运到第j个填方区的土方量，在挖填平衡的原则下进行场地平整时，根据线性规划理论，土方调配方案的优化设计问题，即在土方总运输成本(元)或土方总运输量(m3－m)最小前提下的xij求解问题，可以归结为求解以下约束优化模型:

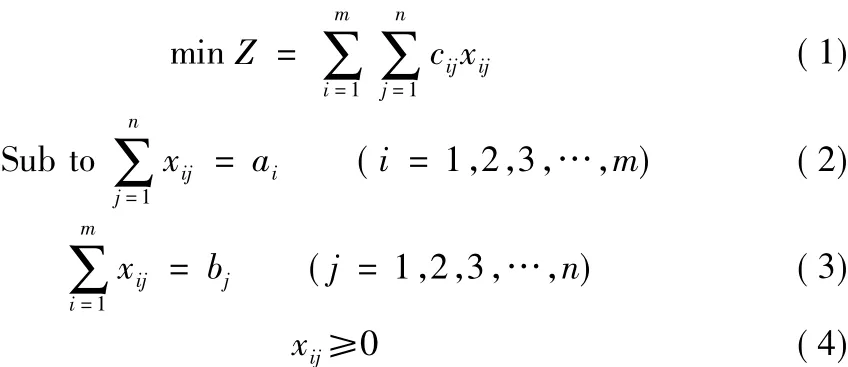
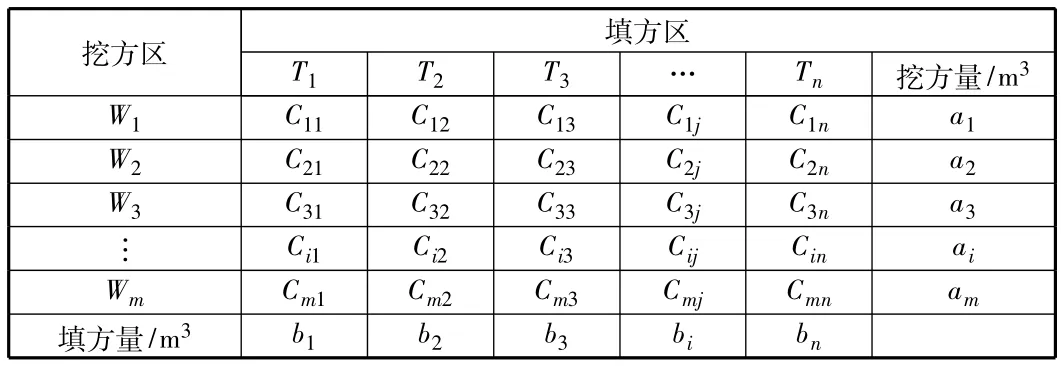
表1 单位运价(或土方运距)及填挖土方量平衡表

式(1)为目标函数，表示优化目标为土方总运输成本(元)或土方总运输量(m3－m)最小;式(2)表示第i个挖方区的挖方量为ai;式(3)表示第j个填方区的填方量为bj;式(4)表示从第i个挖方区调运到第j个填方区的土方量必须符合实际意义，即从第i个挖方区调运到第j个填方区的土方量xij要不小于0。式(1)～式(4)四个数学表达式共同形成了土方调配问题的数学模型。根据挖填平衡的原则，在场地平整过程中总的挖方量等于总的填方量，即，所以其涉及的独立方程个数实际为(m+n－1)个。但由于模型中涉及到m×n个变量，一般在实际情况中，方程组有无穷多组解，其中每一组都能得到(m+n－1)个变量值，而在这无穷多组解中如何获取一组最优的结果便是土方调配的关键所在。实际工程中，表上作业法得到了广泛的应用，但由于应用此方法求解时，往往需要经过多次循环才能找到优化解。对一些复杂的工况，表上作业法的计算效率和精度成为制约此方法应用的难点。应用Matlab的优化工具箱可以快速而准确的找到此类问题的优化解。

3 土方调配方案的Matlab实现

由m个挖方区的挖方量ai和由n个填方区的填方量bj合并组成的列向量用B表示。设:

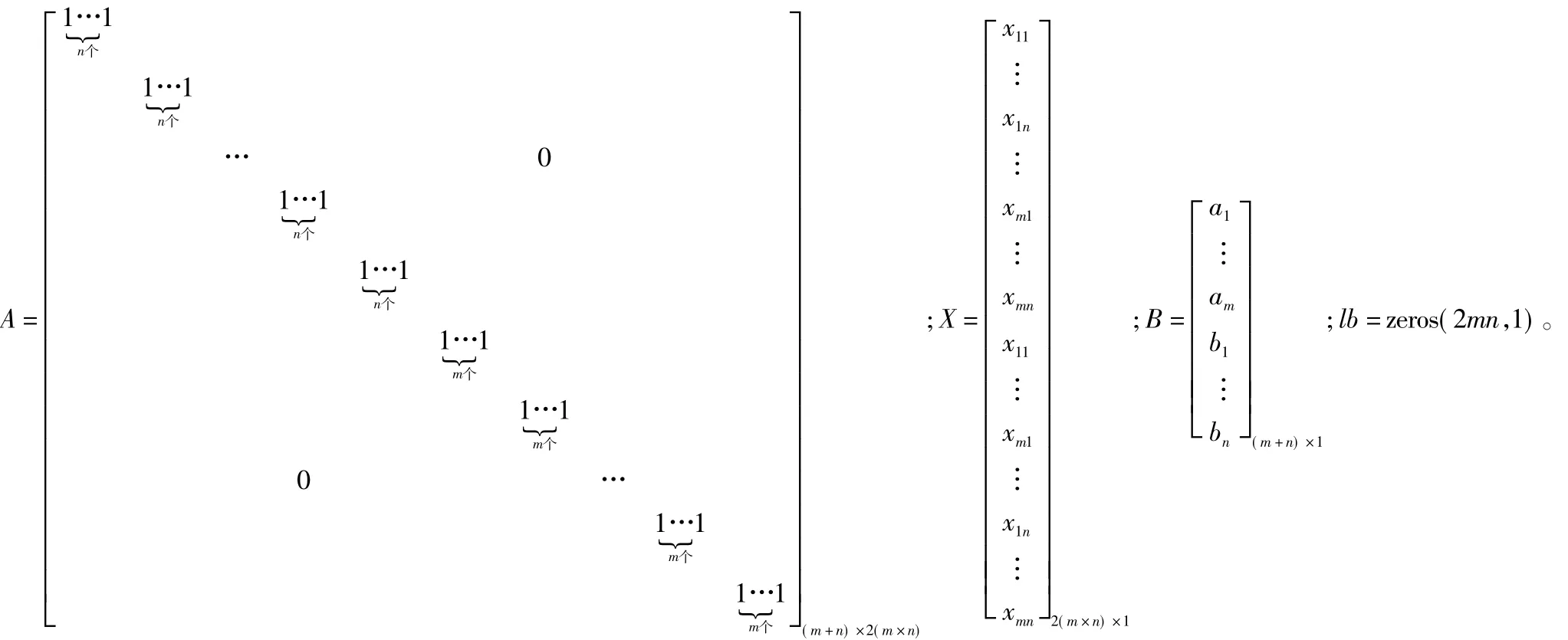
则该优化问题可以表示为如下的Matlab数学问题［5］。

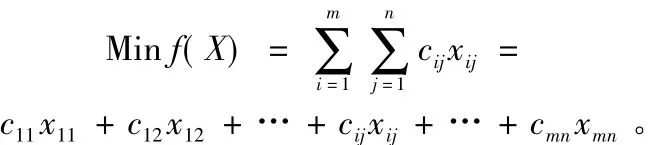
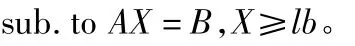
用以下的Matlab命令可以方便的求解土方调配问题的经济优化解。

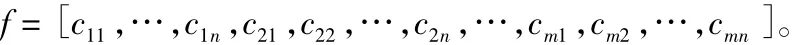
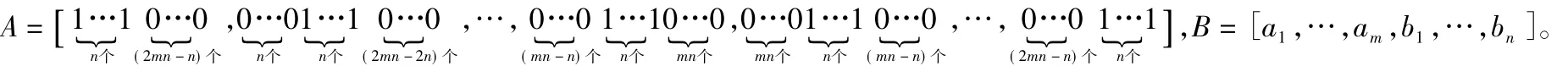
lb=zeros(2mn，1)，［X，fval，exitflag，output，lambda］=linprog(f，［］，［］，A，B，lb)。

4 优化算例

为了便于说明，本文通过一个具体算例［1］来说明土方调配方案的Matlab实现问题。

算例:某施工场地进行平整时，将挖方区分为W1，W2，W3，W4四个区，填方区分为T1，T2，T3三个区，各区间的单位运价及土方挖填量如表2所示。

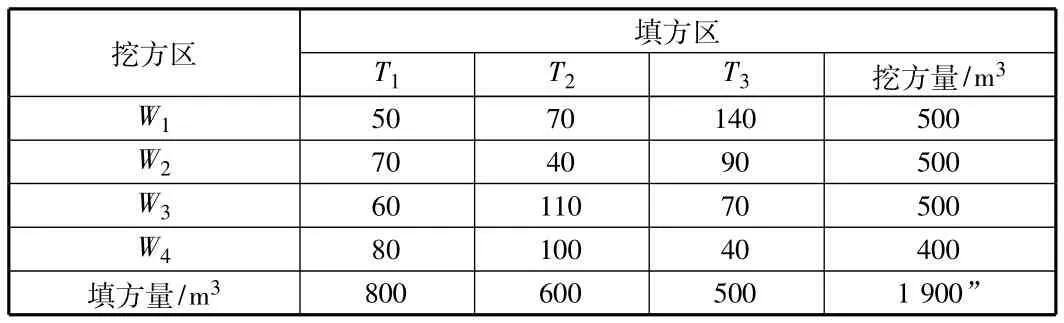
表2 单位运价及土方挖填量表

则该算例的优化问题表示为如下的Matlab数学问题:

Minf(X)=50x11+70x12+100x13+70x21+40x22+90x23+60x31+110x32+70x33+80x41+100x42+40x43。

sub．to AX=B，X≥lb。

用以下的Matlab命令可以方便的求解土方调配问题的经济优化解。

f=［50;70;100;70;40;90;60;110;70;80;100;40］;

A=［111000000000;000111000000;000000111000;000000000111;100100100100;010010010010;001001001001］;

B=［500;500;500;400;800;600;500］;

lb=zeros(12，1);

［X，fval，exitflag，output，lambda］=linprog(f，［］，［］，A，B，lb)。

将以上命令带入Matlab计算器，运行结果如下:

此计算结果与用表上计算法[1]计算的结果相吻合。

5 结语

本文用Matlab提供的优化工具箱对土方调配问题进行了经济优化方案的求解。通过算例表明，将线性规划理论用于Matlab环境中，采用最优化方法进行土方调配方案的优化求解，计算速度较快，计算结果较为精确。

本文的研究成果可以用于指导工程实践，为工程技术人员解决工程实际问题提供了基本方法和思路。

[1] 重庆大学.土木工程施工(上册)[M].北京:中国建筑工业出版社，2003.

[2] 李长安，李新辉.表上作业法优化土方调配方案解析[J].河南水利与南水北调，2010(7):53-56.

[3] 刘大为，张方华.运输问题表上作业法的改进[J].科技资讯，2008(12):87-89.

[4] 曾国勋.最小树求解的表上作业法[J].四川工程职业技术学院学报，2010(2):105-109.

[5] 薛 山.MATLAB基础教程[M].北京:清华大学出版社，2011.