语言混合加权平均距离测度及其在决策中的应用

崔松岩，彭定洪，李楠楠

(1.浙江海洋学院，浙江 舟山 316000;2.哈尔滨理工大学管理学院，哈尔滨 150040)

0 引言

在实际的决策过程中，由于决策问题本身的复杂性和决策环境的模糊性，专家就同一决策问题不能给出方案的精确的数字信息，而是可能使用语言短语给出方案的语言决策信息[1,2]。鉴于语言变量有利于减轻决策过程中决策者的认知压力，利于决策者把握事物的真实状态等优点，对语言评价信息的研究引起了国内外众多专家的重视，并取得大量的研究成果。

距离测度是用于区分两个对象差异的重要工具之一。目前，诸多学者对模糊集、区间数、直觉模糊数、语言变量[3,4]等的距离测度进行了深入研究，并广泛应用到决策、数据挖掘、模式识别等诸多领域。标准汉明距离，加权汉明距离是应用最为广泛的距离测度，它们分别由算术算术平均、加权平均集结而成。最近，受有序加权平均(OWA)算子[5]启发，XU与CHEN[6]提出了有序加权距离测度，该距离测度具有OWA优良性质，因此得到了广泛关注及进一步研究。针对语言变量间的距离，XU[3]定义了两个语言变量的偏离度概念，Merigó与CASANOVAS[4]提出了语言加权平均距离测度(LOWA)。众所周知，加权平均算子(WA)与有序加权平均算子(OWA)的本质区别在权重向量的确定，前者权重用于反映决策者对变量重要程度的判断，而后者则强调变量的序权重用于反映不同的决策策略(规则)或决策者的决策态度。因此，为兼顾加权平均与有序加权平均各自优势，本文在文献[4]基础上提出一种语言混合加权平均距离测度，并简要分析它的优良性质，据此依据理想点思想，给出一种多属性决策方法。

1 预备知识

令S={sα|α=0,1,2,...,τ}为一个具有奇数个元素的语言术语集，它满足以下特征[1]：(1)有序性：sα＞sβ当α＞β；(2)存在逆算子：Neg(sα)=sβ，其中α+β=τ；(3)最大值：如果i≥j，那么max(si,sj)=si，(4)最小值：如果i≥j，那么min(si,sj)=sj。

例如语言术语集S可以定义如下：

S={s0=极差，s1=非常差，s2=差，s3=稍差，s4=一般，s5=稍好，s6=好，s7=非常好，s8=极好}。

为了避免运算过程中的信息损失，文献[2,3]将离散语言术语集 S 拓展为连续语言术语集Sˉ={sα|α∈[0,τ]}。当sα∈S，称sα为原始术语，否则，称sα为虚拟术语。通常，原始术语用于决策者判断，虚拟术语用于运算。

2 混合加权语言距离测度

定义 1[4]令X=(sX1,sX2,...,sXn)与Y=(sY1,sY2,...,sYn)为表征对象X与Y的两组语言变量集，则一个语言有序加权平均距离(LOWAD)测度是一个具有相关权重向量w=(w1,w2,...,wn)，满足的映射LOWAD:Sn×Sn→S：

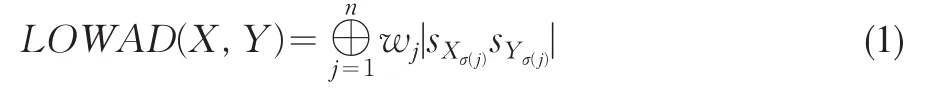
其中(σ(1),σ(2),...,σ(n))为(1,2,...,n)具有|sXσ(j-1)sYσ(j-1)|≥ |sXσ(j)sYσ(j)|特点的排列。

如果定义一个排序ε:(1,2,...,n)→(1,2,...,n)为σ:(1,2,...,n)→(1,2,...,n) 的 逆[7]， |sXj-sYj| 为{|sXj-sYj|,j=1,2,...,n}中第ε(j)大元素，则式(1)也可表示为：

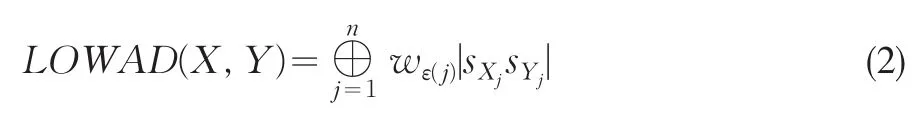
定义2 令X=(sX1,sX2,...,sXn)与Y=(sY1,sY2,...,sYn)为表征对象X与Y的两组语言变量集，则一个语言加权平均距离(LWAD)测度是一个具有重要性权重向量ω=(ω1,ω2,...,ωn)，满足的映射LWAD:Sn×Sn→S：

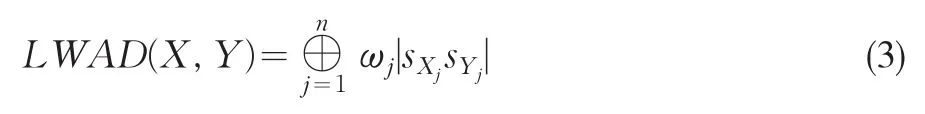
显然，语言加权平均距离(LWAD)测度与语言有序加权平均距离(LOWD)测度的本质区别在权重向量的确定，前者权重用于反映决策者对语言距离分量重要程度的判断，而后者则强调语言距离分量的序权重用于反映不同的决策策略(规则)或决策者的决策态度。因此，为兼顾加权平均与有序加权平均各自优势，下面介绍一种语言混合加权距离测度。

定义3 令X=(sX1,sX2,...,sXn)与Y=(sY1,sY2,...,sYn)为表征对象X与Y的两组语言变量集，则一个语言混合加权平均距离(LHWAD)测度是一个具有相关权重向量w=(w1,w2,...,wn)，满足的映射LHWAD:Sn×Sn→S：

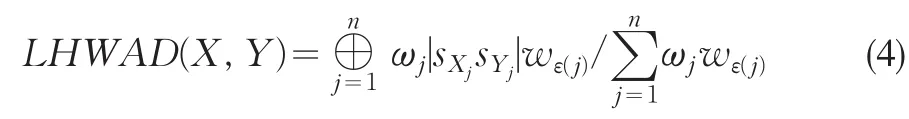
其中ε(̇̇)为一个排列函数，ω=(ω1,ω2,...,ωn)是|sXjsYj|重要性权重，且满足

定理1语言加权平均距离(LWAD)是混合加权语言距离的特殊形式。

定理2有加权平均距离(LOWAD)是混合加权语言距离的特殊形式。

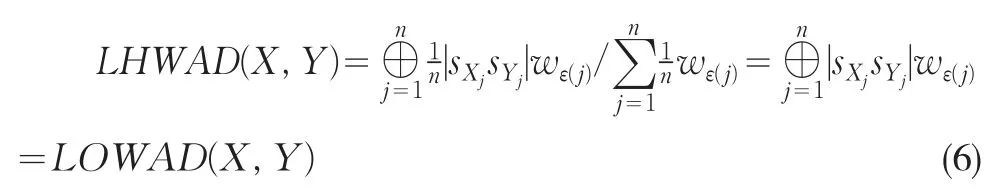
从定理1与2可知，LHWAD测度泛化了LOWAD测度(1)与LWAD测度(3)，因此它兼顾了集结过程中的重要性权重与反应决策策略或决策者态度的序权重。

混合加权语言距离测度有以下性质：

（1）幂等性如果|sXjsYj|=d,j=1,2,...,n，则:

（2）介值性

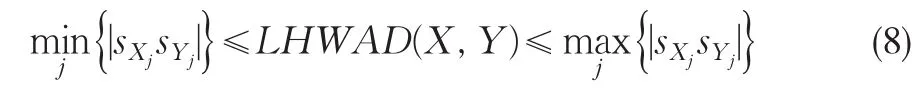
（3）单调性令Z=(sZ1,sZ2,...,sZn)，如果所有|sXjsZj|,j=1,2,...,n，则:

（4）对称性

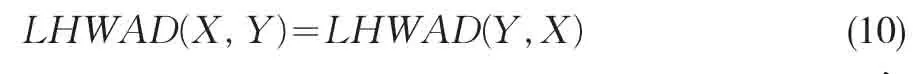
语言距离分量的排序与其序权重向量的确定是混合加权语言距离测度的关键。从一般的排序角度来看，混合加权语言距离(LHWAD)可分为降序LHWAD(D-LHWAD)测度与升序LHWAD(A-LHWAD)测度。设D-LHWAD的序权重为w+j，A-LHWAD的序权重为w-j，则w+j与w-j具有如下关系

对于降序LHWAD测度的序权重向量的确定，最常用且简洁的方法式利用语言量化方法获取[8]，

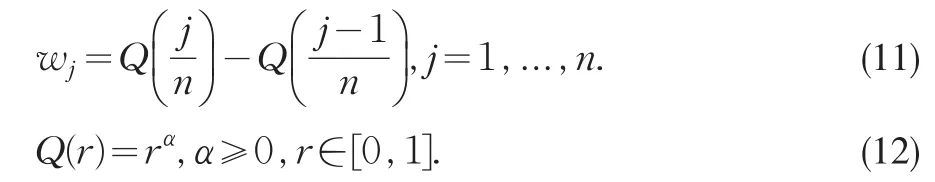
其中参数α为决策策略参数，它通过不同的决策策略语言取值来反应介于“所有”与“至少一个”间距离分量需要被满足不同的决策策略，常见的决策策略及它们相应的参数α取值[9]如表1所示。

表1 决策策略及其参数取值

3 基于LHWAD测度的多属性决策方法

对于多属性决策问题，设m个备选方案Ai(i=1,..,m)依据n个属性xj(j=1,…,n)进行优选或排序，其中属性重要性权重为满足方案的属性值用语言术语形式表达。

下面给出一种基于语言混合加权距离测度的多属性决策方法，具体步骤如下：

（1）确定正负理想解

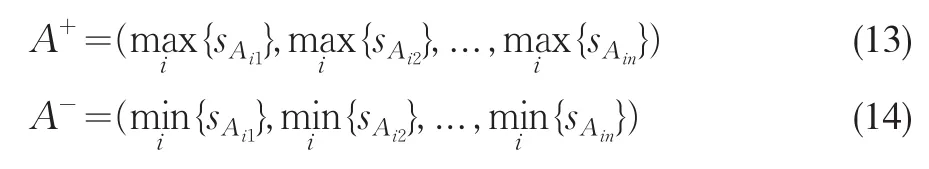
（2）确定决策策略，求取序权重向量

根据实际决策情况，利用语言术语确定决策策略参数α，进而利用式(11)与(12)确定D-LHWAD序权重，利用D-LHWAD与A-LHWAD序权重间关系确定A-LHWAD序权重。

（3）确定正负区分度

根据接近正理想解，远离负理想解为优思想，即距离正理想解越小，距离负理想解越大性能越好。分别利用式

(4)获取决策方案Ai与正/负理想解的正/负语言区分度：

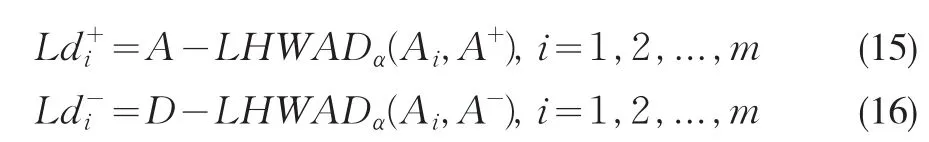
（4）确定方案贴近度

根据方案同时接近正理想解，远离负理想解为优原理，构造语言贴近度：

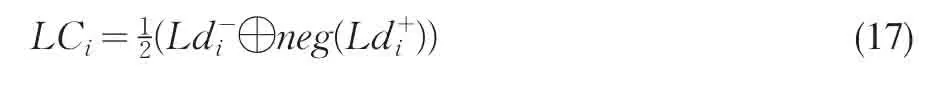
（5）方案排序

根据语言贴近度LCi对方案Ai进行选择排序。

4 算例

考虑某个风险投资企业进行项目投资问题，对5个备选企业A1～A5依据4个评价属性：风险因素(C1)、社会政治影响因素(C2)、环境影响因素(C3)和成长因素(C4)进行排序。为简单起见，假设属性权重向量为ω=(ω1,ω2,ω3,ω4)=(0.1,0.3,0.2,0.4)，每个备选方案对属性的满足程度用语言术语集{s0,s1,s2,s3,s4,s5,s6}={极差,非常差,差,一般,好,非常好,极好}表示，所得的语言评估矩阵为:

下面根据本文所提出的方法进行求解：

步骤1分别利用式(13)和(14)确定正理想方案与负理想方案。

步骤2根据实际情况，确定决策策略参数α=2，即考虑“很多”指标，进而利用式(11)与(12)确定序权重向量。

步骤3分别利用式(15)和(16)，获取各方案正负语言区分度

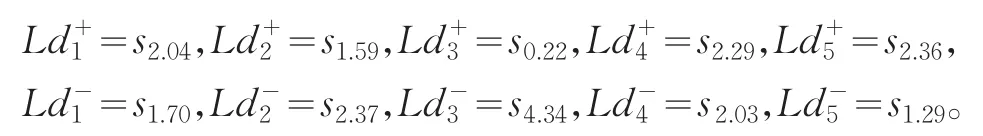
步骤4利用式(17)得到各方案语言贴近度

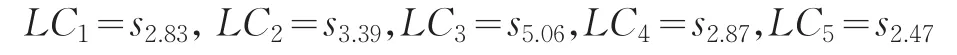
步骤5根据所得贴近度，对决策方案进行排序。

A3≻A2≻A4≻A1≻A5，A3为最优备选方案。

为了证实该法的有效性与优越性，我们再次将语言加权平均距(LWAD)离测度与语言有序加权平均距离(LOWAD)测度应用到本文所提方法中，其结果如表2所示。

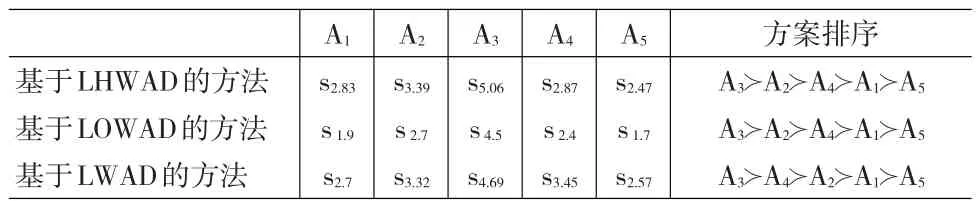
表2 不同语言距离下的决策结果比较

显然，采用三种语言距离测度获取的排序结果基本一致，其最优备选方案均为A3，除采用LWAD获取的结果A4与A2出现逆序，表明该方法的有效性。值得注意的是不同的决策策略得出的序权重向量会对排序结果产生影响，决策策略应根据实际需求选择。

5 结论

本文在语言有序加权平均距离测度[4]基础上，提出了一种混合加权语言距离测度，该距离测度不仅能考虑每个数据自身的重要性程度，而且还能体现该数据所在位置的重要性程度，因而泛化了语言加权距离测度与语言有序加权距离测度，分析了该距离测度的一些优良性质。进而提出了一种多属性决策方法，并通过实例验证了该方法的有效性与可行性。

[1]Herrera F,Alonso S,Chiclana F,et al.Computing with Words in Deci⁃sion Making:Foundations,Trends and Prospects[J].Fuzzy Optimiza⁃tion and Decision Making,2009,8(4).

[2]XU Z.A Method Based On Linguistic Aggregation Operators for Group Decision Making with Linguistic Preference Relations[J].Infor⁃mation Sciences,2004,166(1～4).

[3]XU Z.Deviation Measures of Iinguistic Preference Relations in Group Decision Making[J].Omega,2005,33(3).

[4]Merogój M,Casanovas M.Decision Making with Distance Measures and Linguistic Aggregation Operators[J].International Journal of Fuzzy Systems,2010,12(3).

[5]Yager R R.On Ordered Weighted Averaging Aggregation Operators in Multicriteria Decision-making[J].IEEE Transactions on Systems,Man,and Cybernetics,1988,18(1).

[6]Xu Z,Chen J.Ordered Weighted Distance Measure[J].Journal of Sys⁃tem Science and System Engineering,2008,17(4).

[7]Lin J,Jiang Y.Some Hybrid Weighted Averaging Operators and their Application to Decision Making[J].Information Fusion,2011,(06).

[8]Yager R R.Quantifier Guided Aggregation Using OWA Operators[J].International Journal Intelligent System,1996,11(1).

[9]Malczewski J.Ordered Weighted Averaging with Fuzzy Quantifiers:GIS-Based Multicriteria Evaluation for Iand-use Suitability Analysis[J].International Journal of Applied Earth Observation and Geoinfor⁃mation,2006,8(4).