不规则形状小行星引力场组合建模方案
2012-07-25束磊刘睿张迎春
束磊,刘睿,张迎春
(1.哈尔滨工业大学卫星技术研究所,黑龙江哈尔滨 150001;2.西北工业大学精确制导与控制研究所,陕西西安 710072)
引言
1996年,为探测近地 Eros 433小行星,美国NASA的NEAR项目发射了名为“鞋匠号”(Shoemaker)的探测器。2001年,经过一年的在轨观测,“鞋匠号”成功地在爱神星表面软着陆。之后,欧洲和日本也各自发射了多个小行星探测器。
小行星的引力场模型对于探测器的动力学建模至关重要。由于多数小行星的形状极不规则,其引力场与地球、月球这样的近圆天体有很大差别。天体重力场分析通常采用球谐模型方法[1-4]。但是,球谐模型中假定了一个作为参考的限制球[2]。在限制球外空间,有限阶的球谐展开式能够较为准确地反映小行星引力场的强度和分布;但在限制球内,球谐展开式会发散,无法准确描述真实引力场。为了解决这一问题,本文引入多面体模型法[5-6],尽管该模型存在因为真实小行星密度非恒定引起的误差,但由于该模型在限制球内不存在发散问题,故在限制球内其精度相对于球谐模型更高。文献[7]提到了多面体模型,但也只是将其应用于求解球谐模型的球谐系数,还没有用多面体模型对不规则形状小行星的引力场建模的报道。文献[3]中引力场模型用的是球谐模型,但没有考虑球谐模型的发散问题。
本文结合球谐模型和多面体模型各自的优缺点,提出了一种基于软着陆或超低轨道飞行过程中轨道高度不断变化对引力场模型进行切换的思想,即在分界半径外的引力场用球谐模型计算,分界半径内用多面体模型计算。
1 两种引力场模型
1.1 球谐模型
小行星引力位的球谐展开式为:

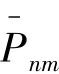
球谐模型中,限制球定义为:球心星体为质心;半径为参考半径Re,通常Re取星体的最大半径。确定各阶球谐系数后,可得到该引力位的解析式:

NASA官网上公布有Eros 433小行星的8阶球谐系数,这些系数是根据探测器得到的数据计算而来的,本文利用这些系数建立球谐模型。但对于不规则形状小行星,当R<Re时,即检验点在限制球内时,式(1)存在(Re/R)n,模型存在发散的可能。
1.2 多面体模型
多面体模型是由若干个小三角形组成的多面体来逼近真实小行星的形状。在假设小行星内部等密度情况下,可通过三重积分近似计算出整个小行星的外引力场强度和分布[6]。由于无法准确得到真实小行星的密度分布,通常将小行星的密度近似为其平均密度[6]。真实小行星密度非恒定会引起一定的误差,但在限制球内其精度相对于发散的球谐模型更高。将小行星等效为内部密度恒定的多面体后,根据文献[6]中的推导,其引力位为:

其中:

U对各坐标轴求导,可求得引力位梯度,其分量即为各坐标轴上的引力加速度。

以上各式中的符号定义如表1所示。

表1 多面体模型中相应符号的定义
以爱神星Eros 433为例,参考NASA官网公布的探测数据,取其表面3 897个点,构成7 790个三角形面,这样构成的多面体能够高度模拟爱神星的真实形状,如图1和图2所示。下文在这一模型的基础上进行仿真计算。

图1 爱神星多面体三维图

图2 爱神星多面体平面图
2 轨道动力学方程
以小行星软着陆为应用目的,本文将探测器绕小行星运动的轨道动力学方程建立在小行星固定坐标系下。首先建立小行星的固定坐标系Oxyz:原点O在小行星质心,z轴为小行星自转轴(最大惯量轴),x轴为最小惯量轴,y轴满足右手定则。
建立惯性坐标系Ox1y1z1:原点O在小行星质心,x1轴平行于小行星赤道面与黄道面的交线,且指向春分点,z1轴为自转轴,y1轴满足右手定则。星体固定坐标系Oxyz和惯性坐标系Ox1y1z1之间的关系如图3所示。

图3 星体固定坐标系和惯性坐标系
设[xyz]T及[x1y1z1]T分别为物体在固定坐标系和惯性坐标系下的坐标。由坐标变换可得:
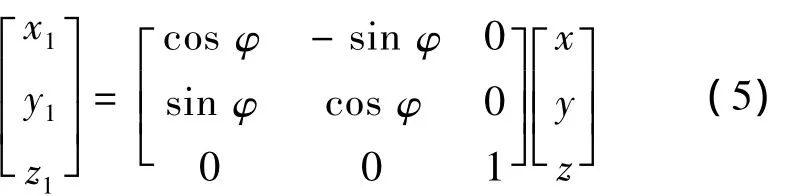
探测器在固定坐标系中的位置、速度和加速度矢量分别为r,r'和r″。
由于小行星自身旋转,故星体固定坐标系为动坐标系,其相对于惯性坐标系的旋转角速度为Ω。假设小行星只绕最大惯量轴旋转,则其旋转角速度在惯性空间的坐标可表示为Ω=[0 0ω]T。由力学知识可得:

式中,aa为绝对加速度;ae为牵连加速度;ar为相对加速度;ac为科氏加速度。其中:
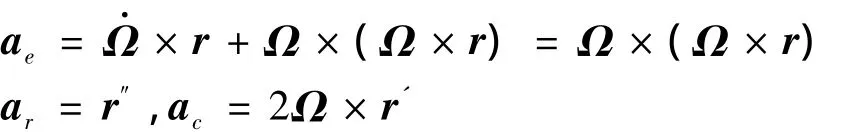
则:

将各坐标代入上式得:

又因为=∂U/∂r,所以,探测器运行的轨道动力学方程为:

爱神星Eros 433绕其最大惯量轴自转,自转角速度约为每天1 639.4°,自转不能忽略。
3 引力场模型仿真对比
3.1 引力加速度对比
以爱神星Eros为例,画出两种模型在不同轨道高度下引力加速度的分布曲线,结果如图4~图6所示。

图4 xy平面初始高度50 km轨道处三种引力加速度对比
从图4可以看出,在高轨道处(初始高度50 km),x,y轴上绕轨一周的加速度变化曲线基本一致,量级在10-7,z轴上有一定的差异,量级为10-10,可以忽略。

图5 yz平面初始高度10 km轨道处三种引力加速度对比

图6 yz平面初始高度10 km轨道处多面体模型与中心引力模型加速度对比
图5表明,在低轨道处(初始高度10 km),应用球谐模型得到的引力加速度变化剧烈,且与多面体模型和中心引力模型加速度差异很大,约为其105倍,说明球谐模型在此轨道处发散。
图6为yz平面内初始高度10 km轨道处多面体模型和中心引力模型的引力加速度绕轨一周的变化曲线。其变化趋势基本一致,说明了多面体模型没有发散问题,应用于低轨是合理的。
3.2 非球形引力作用下探测器轨道变化仿真
设定探测器初始轨道位置及飞行速度,在两种模型的引力场作用下,比较轨道高度的变化。
将惯性坐标系转换为固定坐标系可得:

对方程两边同时求导,得:

假设探测器初始时刻运行在xy平面或yz平面内,设定惯性坐标系下初始条件如表2所示。

表2 探测器在轨运行初始条件
结合轨道动力学方程,利用Simulink搭建仿真模块,仿真得到不受控飞行轨道在两种模型下随时间变化的曲线,如图7和图8所示。
图7为xy平面内50 km轨道的变化曲线,仿真时间为105s。该轨道高度两种模型的x和y坐标基本重合,而z坐标呈周期性变化。轨道半径同样呈周期性变化,且两者变化趋势一致。球谐模型轨道变化约为2.2 km,多面体模型的轨道变化约为1.8 km,差别不大。

图7 xy平面初始高度50 km轨道变化
图8为yz平面内20 km轨道的变化曲线。两种模型坐标初始基本重合,球谐模型的轨道变化很剧烈,当轨道半径降为16 km左右后,呈明显的发散趋势,而此时多面体模型的轨道高度仍然在摄动的作用下缓慢地变化着。

图8 yz平面初始高度20 km轨道变化
由此可见,球谐模型并不适用于小行星附近空间(限制球内),而多面体模型在限制球内还是限制球外都适用。多面体模型计算量较大,利用Matlab仿真耗时较多,但利用C语言等底层语言编程可以显著提高速度,可以实时运算[8],而球谐模型计算更加简便快捷,故针对软着陆或超低空飞行,考虑将两种模型结合起来使用,一般情况下,分界半径比限制球半径稍大。
3.3 分界半径确定
探测爱神星的探测器轨道一般是xy平面内的逆行轨道,本文着重分析两种重力场模型的偏差,通过计算两种模型加速度,可得出两种模型在平面内各个点处的加速度偏差。加速度偏差分布见图9。图中,不同的灰度代表不同的偏差值。

图9 球谐引力场模型与多面体引力场模型加速度偏差分布图
由图9可知,在20 km轨道半径以内,越接近星表,两种加速度模型的偏差越大,故将分界半径取为20 km。在分界半径外,球谐模型能快速准确地计算引力场;在分界半径内,球谐模型是发散的,而多面体模型仍能准确描述小行星外引力场。
4 结论
本文提出了一种小行星引力场组合建模方案,以爱神星引力场模型为例,通过仿真可得以下结论:
(1)在高轨道处(初始高度50 km),多面体模型和球谐模型之间引力加速度误差基本可以忽略,且对不受控探测器轨道摄动影响的差别不大,说明在高轨道处两种模型都能较准确地描述引力场。
(2)在低轨道处(初始高度10 km),球谐模型引力加速度约为多面体模型的105倍,球谐模型在此轨道处发散,说明球谐模型不适用于限制球内低轨卫星轨道。
(3)考虑到球谐模型计算简单快捷但存在发散问题,而多面体模型无发散问题但计算量大,故结合两者的优点,确定了xy平面内的探测器轨道的分界半径取20 km。对小行星引力场建模时,分界半径外空间用球谐模型,分界半径内空间用多面体模型。
[1]Werner R A.Spherical harmonic coefficients for the potential of a constant-density polyhedron [J].Computers and Geosciences,1997,23(10):1071-1077.
[2]Scheeres D J,Williams B G,Miller J K.Evaluation of the dynamic environment of an asteroid:Applications to 433 Eros[J].Journal of Guidance,Control,and Dynamics,2000,23(3):466-475.
[3]Huang X Y,Cui H T,Cui P Y.An autonomous optical navigation and guidance for soft landing on asteroids[J].Acta Astronautica,2004,54(10):763-771.
[4]Miller J K,Konopliv A S,Antreasian P G,et al.Determination of shape,gravity,and rotational state of asteroid 433 Eros[J].Icarus,2002,155(1):3-17.
[5]Cangahuala L A.Augmentations to the polyhedral gravity model to facilitate small body navigation[R].AAS-05-4185,2005.
[6]Werner R A,Scheeres D J.Exterior gravitation of a polyhedron derived and compared with harmonic and mascon gravitation representations of asteroid 4769 Castalia [J].Celestial Mechanics and Dynamical Astronomy,1997,65(3):313-344.
[7]张振江,崔祜涛,任高峰.不规则形状小行星引力环境建模及球谐系数求取方法[J].航天器环境工程,2010,27(3):383-388.
[8]Gregory Lantoine.Optimal trajectories for soft landing on asteroids[R].AE8900 MS Special Problems Report,Space Systems Design Lab,2006.
