一种虚拟目标点的弹道迭代确定方法

王继平，肖龙旭，王安民，林红斌，杜林峰

（1.第二炮兵装备研究院，北京 100085；2.中国人民解放军96271部队，河南 洛阳 471000）

引言

为了提高弹道导弹的精度，一方面要提高导航设备的精度，另一方面要采用先进的制导方法，减小制导方法误差。基于虚拟目标点的闭路制导方法是一种高精度的显示制导方法，它首先要确定虚拟目标点。传统虚拟目标点的确定是基于标准弹道，对地球扁率和再入阻力影响进行修正，但存在百米左右的修正误差［1］。当实际弹道偏离标准弹道，虚拟目标点变化较大时，采用标准弹道确定的虚拟目标点进行闭路制导会产生较大的方法误差。若是处于弹道设计阶段，在标准弹道闭路制导段还没有确定的情况下，传统方法失去了标准弹道关机点基准，确定不了虚拟目标点。

本文的弹道迭代确定方法却能适应这一情况，精确确定虚拟目标点。在飞行过程中，可采用自由飞行弹道的快速计算方法，实时迭代计算虚拟目标点，保证了虚拟目标点相对实际弹道的精度。

1 虚拟目标点的弹道迭代计算思想

虚拟目标点弹道迭代计算分为射前标准弹道迭代和弹上实时迭代计算。射前标准弹道迭代计算量大，计算时间相对较长。文献［2-3］分别对标准弹道迭代作了相关研究，虽然文献［3］的弹道迭代效率较高，但是目前的弹载计算机仍无法实现弹上实时计算，况且对于虚拟目标点的迭代计算，文献［3］的方法不再适用。本文采用类似文献［2］的弹道迭代方法进行虚拟目标的确定，其精度相对标准弹道高得多。弹上实时迭代计算要求计算量小，因而采用自由段飞行弹道的快速计算方法，且弹上采用高性能计算机，才能保证实时性要求。虚拟目标点确定精度由自由段飞行弹道计算精度和再入阻力实时修正精度决定。

射前标准弹道迭代计算思想为:虚拟目标点一般离真实目标点不远，首次弹道计算时可以假设虚拟目标点位于目标点，之后按修正的虚拟目标点进行计算。在闭路制导段进行需要速度增量计算，并进行导引和关机控制，再经过被动段弹道解算落点，通过大地贝赛尔反解［2］求取落点偏差。然后根据落点偏差信息反复修正虚拟目标点，直到落点偏差为零，此时对应的虚拟目标点就是要求的虚拟目标点，同时也确定了闭路制导段。

弹上实时迭代计算思想为:在飞行过程中，当导弹离关机点不远时，对虚拟目标点进行实时迭代修正。以当前需要速度、位置、导弹飞行时间作为关机状态，利用自由飞行弹道的快速计算方法，计算地球扁率对落点的影响；采用拟合方法计算再入阻力对落点的影响；对两者进行修正确定新的虚拟目标点，再以新的虚拟目标点迭代计算需要速度；依此法再次确定虚拟目标点，比较相邻两次虚拟目标点的经纬差，当小于要求值时，迭代结束，即得到当前状态对应的虚拟目标点。

下面首先给出闭路制导的需要速度计算方法和导引关机控制策略，在此基础上探讨虚拟目标点的弹道迭代确定方法。

2 闭路制导导引与关机控制

2.1 闭路制导需要速度计算

闭路制导需要速度是根据导弹当前状态和虚拟目标点，通过椭圆弹道迭代求取的。需要速度可以固定关机点倾角、被动段飞行时间、再入倾角等为条件进行迭代，本文拟采用固定关机点倾角为条件，具体迭代计算公式见文献［1］。

2.2 闭路制导导引

闭路制导方法常在大气层外使用，仅由推力提供视加速度。为了使导弹耗能最少，按“方向与速度增量Δva一致”的原则进行导引控制。设导弹制导控制周期为T，推力沿弹体轴向，则推力控制方向为:

式中，φa，ψa，γa为弹体系相对发射惯性坐标系的绝对俯仰角、绝对偏航角和绝对滚动角；vgxa，vgya，vgza为需要速度增量在发射惯性坐标系下的分量。

2.3 闭路制导关机控制

关机控制采用如下关机条件:

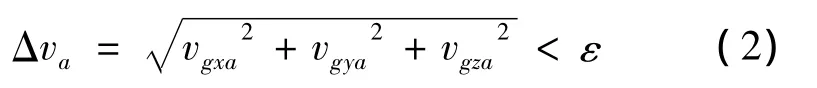
式中，ε为一实际要求的小量。

3 虚拟目标点的标准弹道迭代计算

导弹虚拟目标点的标准弹道迭代计算在射前完成，弹道解算采用龙格-库塔转阿达姆茨数值积分法，在闭路制导段按式（1）和式（2）进行导引和关机控制，弹道迭代参数为虚拟目标点经纬度（LM，BM）。其迭代方法与步骤如下:

（1）令当前虚拟目标点经纬度等于目标点经纬度（LT，BT）:

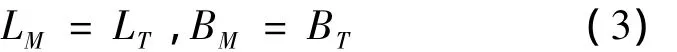
（2）计算以当前虚拟目标闭路制导产生的落点偏差（ΔL，ΔH）对（LM，BM）的偏导数矩阵。

分别给（LM，BM）一个小扰动（δLM，δBM），得:

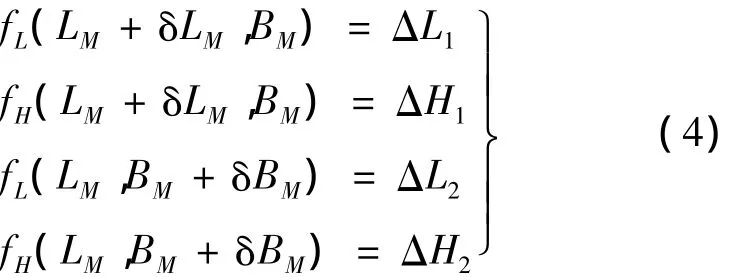
根据上式，落点偏差（ΔL，ΔH）对（LM，BM）的偏导数矩阵为:

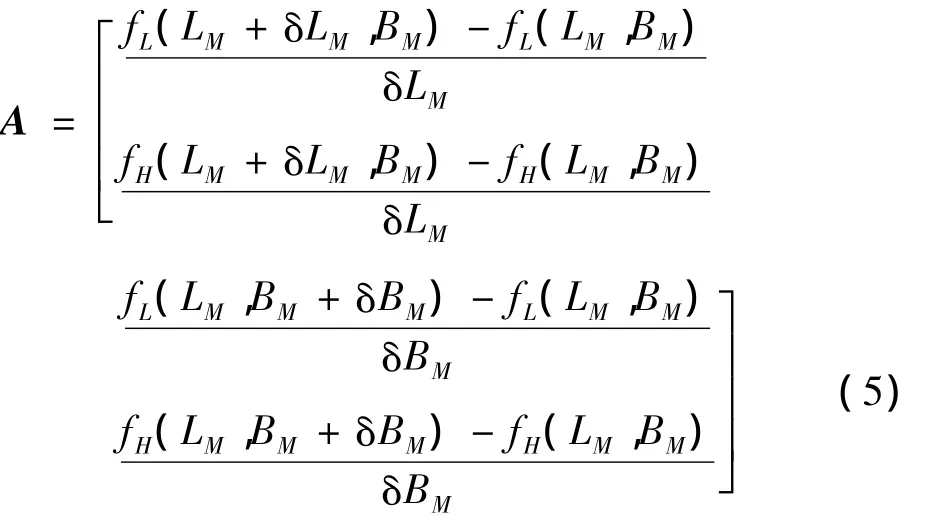
（3）计算当前虚拟目标改变量（ΔLM，ΔBM）

设虚拟目标变化了（ΔLM，ΔBM）后，落点偏差为零，则:

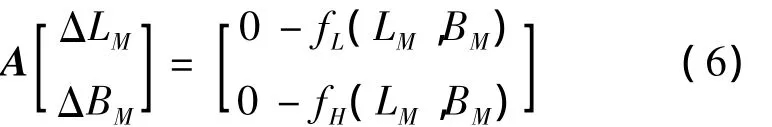
根据式（6），得:

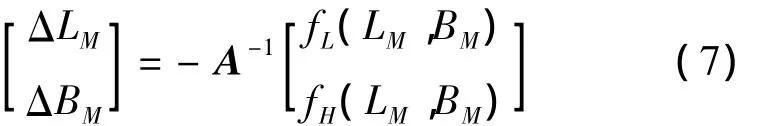
（4）计算以虚拟目标（LM+ΔLM，BM+ΔBM）进行闭路制导产生的落点偏差；

（5）以LM=LM+ΔLM，BM=BM+ΔBM为当前虚拟目标，重复步骤（2）～（4），直至落点偏差ΔL＜ε1，ΔH＜ε2（ε1，ε2为要求小量），此时对应的（LM，BM）即为迭代确定的虚拟目标点。

4 虚拟目标点的弹上迭代实时计算

导弹虚拟目标点的弹上实时迭代计算，采用自由飞行弹道的快速计算方法确定地球扁率影响，采用拟合计算方法确定再入阻力影响，在闭路制导段按式（1）和式（2）进行导引和关机控制，弹道迭代参数为虚拟目标点经纬度（LM，BM）。首先给出自由飞行弹道的快速计算方法和再入阻力影响的实时修正方法。

4.1 自由飞行弹道的快速计算方法

常用的自由飞行弹道的快速计算方法有:自由段弹道解析解的非正交分解法［4-6］、中间轨道法［7］和基于状态空间摄动的自由段弹道解析法［5-6］等。其中非正交分解法的落点偏差精度在百米左右；中间轨道法、基于状态空间摄动的自由段弹道解析法落点偏差计算精度都在40 m以内［5］。可根据需要选择相应的自由段弹道快速计算方法，分别令地球扁率系数J为常值和J=0，计算落点偏差，即为地球扁率对落点的影响。

4.2 再入阻力影响的实时修正方法

当导弹再入大气层后，要受到空气动力的作用。假定弹头是静稳定的，弹头烧蚀是均匀的，即是轴对称的，则可认为再入段导弹的攻角为零。再入段气动阻力的影响是再入点高度、再入点速度、弹道倾角及弹头的阻重比的函数。若导弹型号已定，弹道倾角固定，则再入阻力影响只是落速和再入点高度的函数，可将射程角偏差（Δβx）拟合成再入点速度Vc、再入点高度hc的函数［8］。

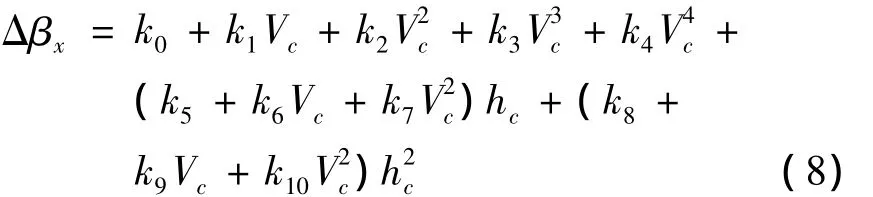
式中，ki（i=0，…，13）为拟合系数。从而可根据射程角偏差确定落点经纬度偏差:

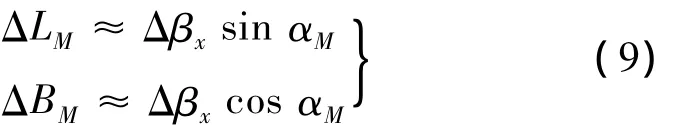
式中，αM为落点射向方位角。

4.3 弹上迭代实时计算方法与步骤

虚拟目标点的弹上迭代实时计算方法与步骤如下:

（1）以真实目标点为虚拟目标点（LM1，BM1），计算需要速度vRxa，i，vRya，i，vRza，i，其中，vRxa，i，vRya，i，vRza，i为需要速度在发射惯性坐标系下的分量，下标i代表弹上制导周期数；

（2）以需要速度和当前位置、时间为当前状态，采用自由飞行弹道的快速计算方法计算再入速度和地球扁率引起的落点偏差（ΔLM1，ΔBM1）；

（3）将再入速度和再入高度代入拟合公式（8），计算再入阻力引起的落点偏差（ΔLM2，ΔBM2）；

（4）对地球扁率和再入阻力引起的落点偏差进行修正，获得虚拟目标点:

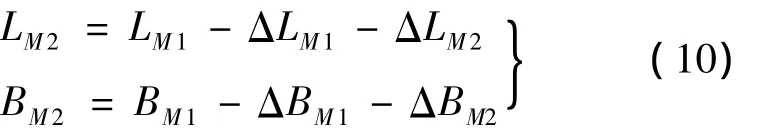
（5）当|LM，j+1－LM，j|＜ε1，|BM，j+1－BM，j|＜ε2（j=1，2，…，n）时，停止迭代；否则以虚拟目标点（LM2，BM2）计算需要速度vRxa，i，vRya，i，vRza，i，转入（2）。

5 仿真算例及结果分析

5.1 算例条件

5.2 算例结果

经仿真计算，标准弹道迭代经两次迭代修正后达到迭代要求。虚拟目标弹上迭代计算的每个制导周期经过两次迭代达到迭代要求。仿真计算机平台为CPU主频2.83 GHz，四核处理器；内存3.37 G；操作系统Windows xp2，采用C语言在VC++6.0编程环境下运行迭代代码耗时0.141 ms，可见在高性能计算机上实现实时计算是可能的。

虚拟目标点迭代结果见表1。

表1 虚拟目标点迭代结果

由表1可知，按迭代后的虚拟目标点进行闭路制导，落点偏差在1 m内。

按最终的虚拟目标进行闭路制导，其导弹速度（Vx，Vy，Vz）和需要速度（Vrx，Vry，Vrz）随时间的变化曲线见图1，俯仰角、偏航角随时间的变化曲线见图2，俯仰角、偏航角迭代终值与初值之差（Δφa，Δψa）随时间的变化曲线见图3。

由图3可知，随虚拟目标点变化，闭路制导的俯仰角、偏航角也随之变化。虚拟目标点迭代确定后，闭路制导段也同时确定。

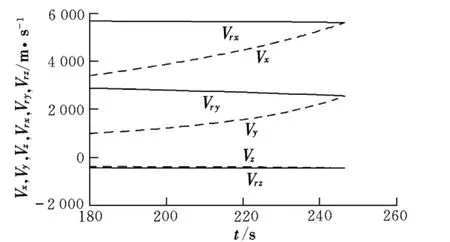
图1 导弹速度和需要速度随时间的变化曲线

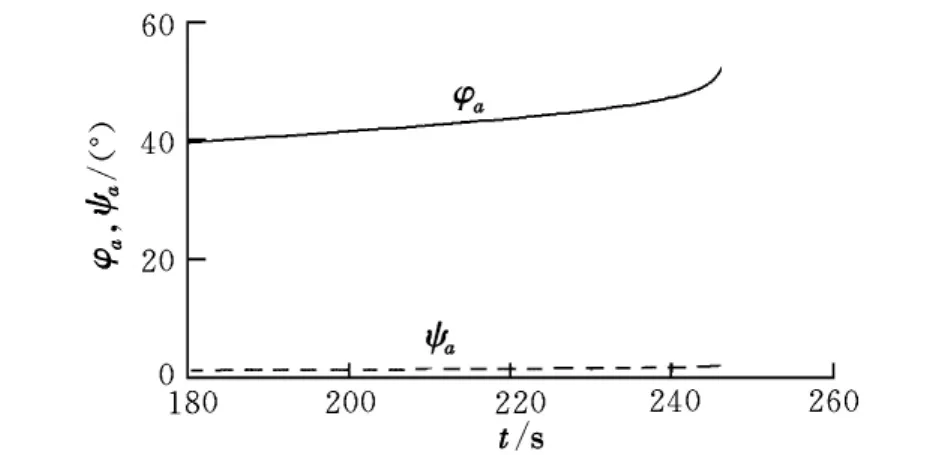
图2 φa和ψa随时间的变化曲线

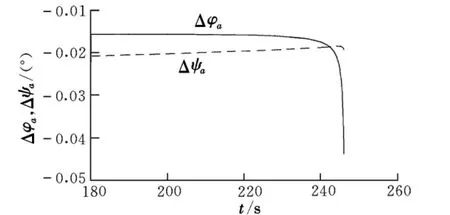
图3 Δφa和Δψa随时间的变化曲线

当实际弹道与标准弹道偏离不大时，射前标准弹道迭代确定的虚拟目标点精度高，按其进行闭路制导，方法误差在80 m内；当导弹推力产生大偏差时，实际弹道偏离标准弹道很大，按射前装订的虚拟目标点进行闭路制导误差达300 m以上，在飞行过程中采用实时迭代计算的虚拟目标点进行闭路制导，落点误差可精确到100 m左右。虚拟目标点实时迭代计算随时间的变化曲线如图4所示。

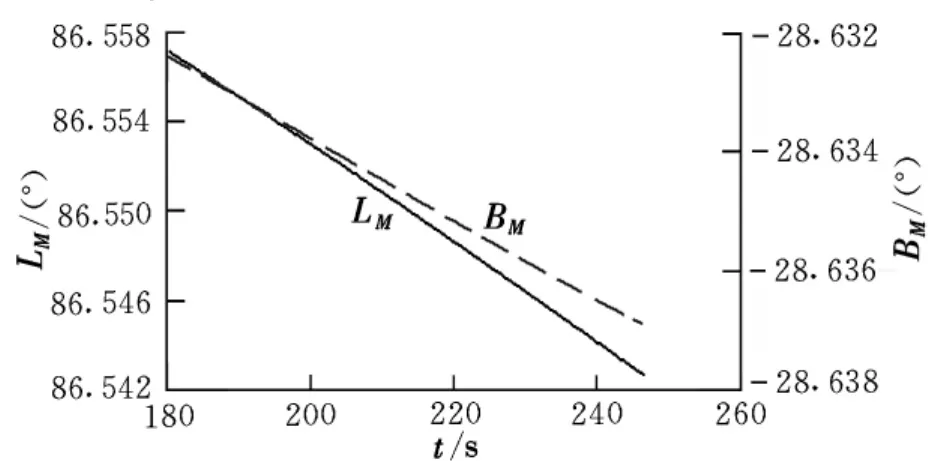
图4 虚拟目标随时间的变化曲线

可见，在闭路制导段开始与结束虚拟目标点变化较大，而起关键作用的是最终的虚拟目标点，因而整个闭路制导段实时迭代计算虚拟目标点没有必要，只需在关机前一小段时间进行迭代计算实时修正即可，之前用地面装订虚拟目标诸元制导。

6 结束语

虚拟目标点的射前标准弹道迭代确定方法，在闭路制导段设计时能够有效发挥其作用，并能根据迭代要求达到所需精度。但由于需要解算弹道，且进行弹道迭代，因而比虚拟目标点的传统确定方法耗时。虚拟目标点的弹上迭代实时计算方法，由于采用迭代思想同样能根据迭代要求达到所需精度，但精度限于自由飞行弹道的快速计算精度和再入阻力影响的修正精度。实际使用中，为减小弹上计算负荷，闭路制导段可先按射前装订的虚拟目标点进行制导，到关机点前几秒时，采用虚拟目标点实时迭代计算，根据弹载计算机性能可适当加大迭代计算周期，按实时计算的虚拟目标点进行闭路制导，以提高制导精度。

［1］王继平，王明海.基于虚拟目标点制导的误差分析［J］.飞行力学，2007，25（4）:50-53.

［2］马丹山，王明海，车明波.弹道导弹的标准弹道迭代方法研究［J］.飞行力学，2007，25（4）:48-53.

［3］王明海，李邦杰.弹道导弹弹道设计的一种快速迭代方法［J］.飞行力学，2007，25（2）:76-77.

［4］张毅，肖龙旭，王顺宏.弹道导弹弹道学［M］.长沙:国防科学技术大学出版社，2005.

［5］李连仲.弹道飞行器自由飞行轨道的解析解法［J］.宇航学报，1982，3（1）:1-17.

［6］郑伟.地球物理摄动因素对远程弹道导弹命中精度的影响分析及补偿方法研究［D］.长沙:国防科学技术大学，2006.

［7］刘林.人造地球卫星轨道力学［M］.北京:高等教育出版社，1992.

［8］肖龙旭，王顺宏，魏诗卉.地地弹道导弹制导技术与命中精度［M］.北京:国防工业出版社，2009.