鸭式旋翼/固定翼飞机过渡模式控制律设计

黄晶，李俨，赵凯瑞，张梦妮

（西北工业大学自动化学院，陕西西安 710129）

引言

鸭式旋翼/固定翼（Canard Rotor/Wing，CRW）飞机是有别于常规直升机和常规固定翼飞机的一类新型飞行器。鸭式旋翼/固定翼飞机采用先进的CRW理念［1］设计，其最显著的特征是装有一副既可高速旋转作旋翼又可停转锁定作固定翼的旋翼/固定翼，这使得该机既能像直升机那样垂直起降低速飞行，又能像固定翼飞机那样高速巡航飞行。

CRW飞机具有三种工作模式:直升机模式、固定翼模式和过渡模式［1］。在低速飞行时以直升机模式工作，高速飞行时以固定翼模式工作，在直升机模式和固定翼模式之间存在着过渡模式。CRW飞机在直升机模式和固定翼模式时可以分别按照直升机和固定翼飞机的控制方法进行控制，但是过渡模式存在强非线性和控制输入转移等问题，所以研究CRW飞机平稳过渡问题具有十分重要的意义。

1 飞机模型的建立

图1为典型的CRW飞机X-50A的左前视图。该机机头前部装有鸭翼，用于抵消飞机在高速运动时尾部平尾的升力力矩。其主要气动部件包括旋翼操纵面和固定翼气动面两部分［2-3］。旋翼操纵面包括总距、纵向周期变距和横向周期变距；固定翼操纵面包括鸭翼、水平尾翼和垂尾。

飞机小扰动方程能较好地反映飞机的开环特性并适用于控制律的设计。在过渡模式，飞机速度跨度范围较大，而小扰动方程仅在状态量变化较小的范围内适用，故需要建立能准确反映过渡模式飞机气动特性并能适用于过渡模式仿真的非线性数学模型。本文首先建立CRW飞机的非线性数学模型，然后进行小扰动线性化得到飞机的线性模型（其中非线性方程用于进行过渡模式仿真，小扰动方程用于进行控制律设计）。

1.1 纵向非线性模型

CRW飞机纵向非线性数学模型［4-5］建立如下:

式中，V，θ，ωz，α，H分别为速度、俯仰角、俯仰角速度、迎角和高度；m，Iz和g分别为飞机质量、飞机绕机体轴的转动惯量和重力加速度；FT，L，D，Mz分别为发动机推力、升力、阻力和俯仰力矩。

1.2 “小扰动”线性化模型

对非线性方程进行小扰动线性化［6］，线性化后结果如下:

式中，X为飞机状态量，X=［V，α，ωz，θ，H］T；Ai和Bi为系数矩阵，i=1，…，6分别代表6个不同速度状态点；U为控制输入量，U=［δH，δC，φ7，θ2，PT］T，其中δH，δC，φ7，θ2，PT分别为气动面平尾偏角、鸭翼偏角、旋翼总距、旋翼纵向周期变距和尾部螺旋桨发动机推进功率。

1.3 配平

在进行过渡模式控制律设计前还需考虑飞机的平衡问题，即计算飞机初始发动机功率、旋翼总距、平尾偏角的初始值，保证飞机作直线平飞运动。另外，CRW飞机在进入过渡模式时，因为飞机的控制具有冗余操纵面，在某个工作点的配平控制输入值并不唯一。本文采用收敛速度较快的二分法进行配平。将鸭翼和旋翼纵向周期变距设为固定值（δC=12°，θ2=0°），通过二层嵌套的循环程序，分别用δH配平俯仰力矩，用φ7，PT配平升力和阻力，经过计算机反复循环计算，最终得到不同速度的平衡点。

2 过渡模式控制律设计

过渡模式过程如下:飞机尾部安装螺旋桨，螺旋桨推进加速，飞机在低速时升力主要靠旋翼提供，随着飞机速度增大，在平尾和鸭翼上的升力不断增加，旋翼上的升力负担减小；另一方面，平尾和鸭翼上的升力力矩大小相等，方向相反，飞机同时能保证俯仰姿态稳定。当飞机速度达到转换速度Vt时，在鸭翼和平尾上的升力和正好略大于飞机重力，旋翼升力负担为0，这时候旋翼逐渐停转直至锁定，即完成飞机的模式过渡。

2.1 总体设计方案

本文中CRW飞机控制结构由速度控制回路、俯仰姿态控制回路和高度控制回路组成。控制律总体设计方案如图2所示。

图2 CRW飞机控制律总体设计框图

2.2 控制律设计

速度输入信号采用匀加速输入，其表达式为:

式中，VR为飞机参考速度输入信号；V0为飞机初始速度；a为飞机加速度；t为时间。

尾部螺旋桨功率:

式中，PT为尾部螺旋桨功率输入；V为速度测量值（由飞机非线性模型解算得到）；KP－PT为速度控制律的比例系数；PT－trim为尾部螺旋桨功率配平值。

旋翼总距:

式中，ωH－φ7为总距高度误差权重；HR为参考高度输入信号；H为高度测量值（由飞机非线性模型解算得到）；KP－φ7和KD－φ7分别为总距高度控制律的比例系数和微分系数；φ7－trim为总距配平值。总距高度控制律采用PD控制。

旋翼纵向周期变距:

式中，ωθ－θ2为纵向周期变距俯仰角误差权重；θR为俯仰角参考输入信号；θH为高度误差引起的俯仰角输入；θ为俯仰角测量值（由飞机非线性模型解算得到）；KP－θ2和KD－θ2分别为纵向周期变距控制律的比例系数和微分系数。纵向周期变距控制律采用PD控制。

平尾偏角:

式中，ωθ－δH为平尾俯仰角误差权重；KP－δH和KI－δH分别为平尾控制律的比例系数和积分系数；δH－trim为平尾配平输入。平尾控制律采用PI控制。

高度误差产生的俯仰角输入:

式中，ωH－δH为平尾高度误差权重；HR为高度参考输入信号；H为高度测量值（由飞机非线性模型解算得到）；KP－θH和KD－θH分别为平尾高度控制律的比例系数和微分系数。平尾高度控制律采用PD控制。

鸭翼偏角:

2.3 指数控制输入权重分配

高度误差和俯仰角误差控制输入权重分配律均采用指数形式，由以下公式计算得到:

高度误差指数控制输入权重分配原理如图3（a）所示。随着速度增大，输入给平尾的高度误差权重由0逐渐增加到1，平尾控制作用逐渐增强；输入给总距的高度误差权重由1逐渐减小到0，总距控制作用逐渐减小，旋翼逐渐卸载。

俯仰角误差控制输入权重分配如图3（b）所示。输入给平尾的俯仰角误差权重由0逐渐增加到1，平尾控制作用逐渐增强，输入给纵向周期变距的俯仰角误差权重由1逐渐减小到0，旋翼逐渐卸载。

图3 指数权重控制输入分配曲线

3 仿真结果及分析

针对CRW飞机非线性模型分别进行从直升机模式过渡到固定翼模式（加速过渡）的仿真结果如图4所示。

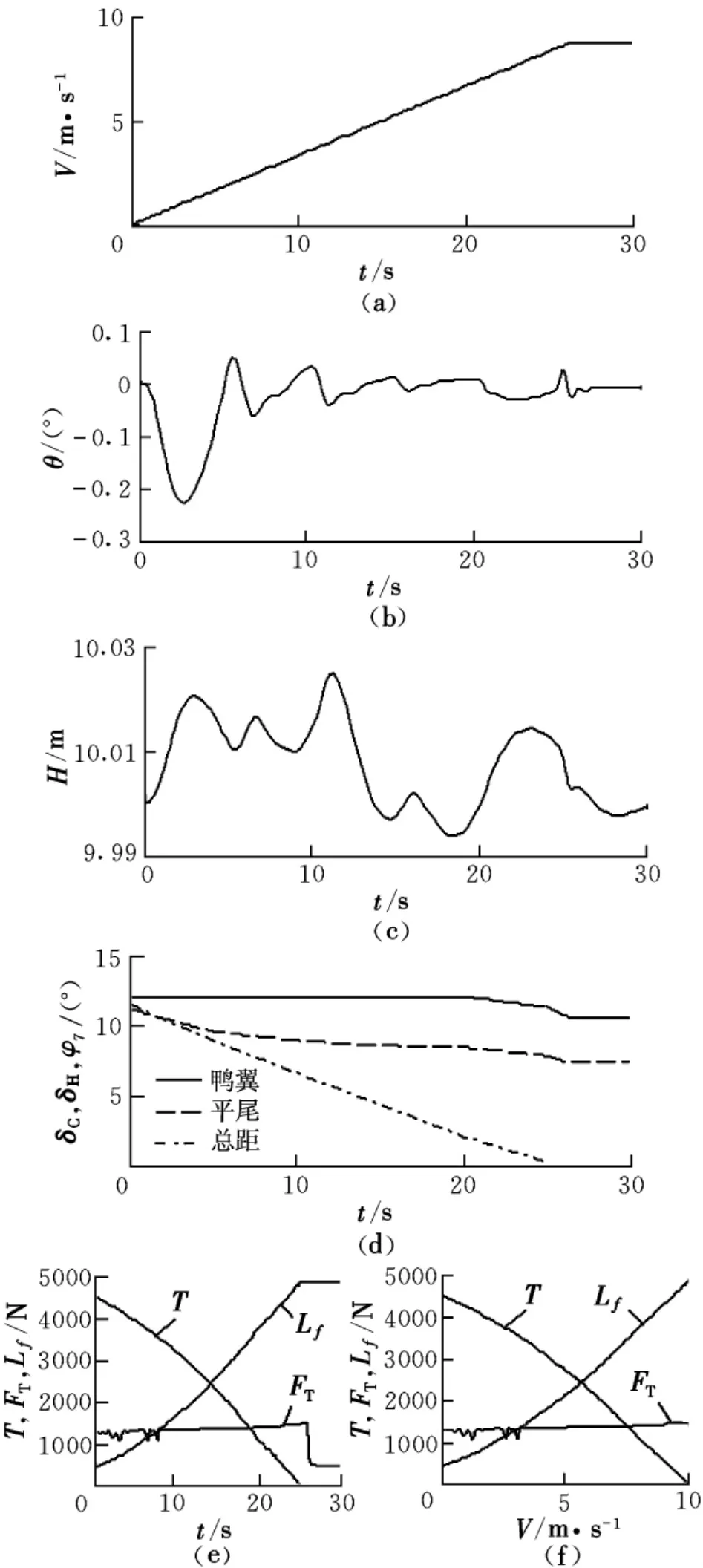
图4 过渡模式控制律仿真曲线

从图4（a）可看出，CRW飞机在整个过渡过程一直作匀加速运动，飞机加速较平稳。从图4（b）和（c）可看出，飞机在过渡过程俯仰角θ变化范围为［－0.25°，0.05°］，高度H的变化范围仅为［9.99，10.03］m，在整个过程中θ和H的抖动范围很小，飞机一直作直线平飞运动。在过渡过程中随着飞机速度增大，旋翼总距的控制输入权重和配平输入值均逐渐减小，总距输入值（图4（d））逐渐减小，当t=25 s时（V=Vt）总距减小为0，旋翼完全卸载。平尾控制输入权重随着速度增大逐渐增大，而平尾输入值（图4（d））逐渐减小，这是因为随着飞机前飞速度增大，平尾舵面效率增大，较小的平尾偏角就能提供所需要的俯仰力矩。图4（e）和（f）表明，在整个过渡模式，随着飞机速度增加，旋翼提供的升力（T）逐渐减小到0，固定翼提供的升力（Lf）逐渐增加直至能完全抵消重力，整个过渡模式的过渡时间大概需要25 s。

4 结束语

本文针对CRW飞机提出控制律总体设计方案和指数控制输入权重分配方法。经仿真验证，本文所提出的方法能有效地保证飞机过渡模式的航迹高度和俯仰姿态的稳定，具有一定的工程实用价值。但是，本文仅进行了直升机向固定翼模式过渡的数字仿真，并未进行固定翼模式向直升机模式过渡的数字仿真。另外，也没有考虑飞机模型不确定性和外加风干扰情况，后续应该考虑以上情况来验证控制律的鲁棒性。

［1］Mitchell C，Vogel B.The canard rotor wing（CRW）aircraft:a new way to fly［R］.AIAA-2003-2517，2003.

［2］Osder S S，Thompson T L.Flight control systems and methods for a jet powered tri-mode aircraft［P］.US:5951608，1999.

［3］邓阳平，高正红，詹浩.鸭式旋翼/机翼飞机的技术发展及其关键技术［J］.飞行力学，2006，24（3）:1-4.

［4］高正，陈仁良.直升机飞行动力学［M］.北京:科学出版社，2003.

［5］卢京潮.自动控制原理［M］.西安:西北工业大学出版社，2004.

［6］吴森堂，费玉华.飞行控制系统［M］.北京:北京航空航天大学出版社，2005.