基于改进不动点的多操纵面飞机重构控制分配

池程芝，章卫国，高亚奎，2，刘小雄，张竞凯

（1.西北工业大学自动化学院，陕西西安 710072；2.中航工业西安飞机设计研究所总师办，陕西西安 710089）

引言

在航空航天领域中，越来越多的飞行器由于多操纵面以及推力矢量技术的应用，具备了较多的气动控制余度，飞行器操纵面的控制方式和组合方式也不再唯一［1］，这使得控制系统的设计难度和复杂性大大增加，但也给重构飞行控制带来了冗余性。控制分配通过合理、有效地分配多种操纵面，使飞机能够适应不同的飞行条件和完成不同的飞行任务，实现不同的飞行控制系统性能目标；同时在飞机操纵面发生故障的情况下，仍然能够通过对剩余多操纵面的重新协调分配来实现控制飞机运动，保持飞机的正常动态性能，提高飞机对故障及损伤的鲁棒性。该技术是解决冗余控制量最优分配的有效方法，已被广泛应用于先进战斗机、民用客机、导弹、航天器等领域［2］。

在控制分配的几类方法［3］中，伪逆法具有计算量小和易于实现等优点，但没有考虑操纵面的饱和（位置和速率）约束限制。近年来的研究热点越来越集中于考虑操纵面饱和约束的情况［4-5］。不动点迭代是一种基于二次规划的控制分配方法，在多操纵面飞机的控制分配问题中应用较多，且已取得了良好的效果［6-7］。但是，考虑到飞控系统对控制分配尤其是容错重构控制分配算法的实时性要求，有必要对不动点迭代的快速改进方法进行研究。本文在不动点迭代过程中探索其沿最大梯度下降方向修正和伪逆法混合的策略，并将改进方法应用于多操纵面飞机的重构控制分配。最后通过仿真验证，表明了该改进方法的快速性和有效性。

1 混合最大方向导数不动点迭代

本节首先对基本不动点和最大方向导数（Max Direction Derivative，MDD）不动点方法进行论述，进而阐述混合MDD不动点迭代方法及其收敛性。

1.1 基本不动点迭代方法

基于二次规划的控制分配问题可描述为［3，6-7］:

设对任意的u=［u1，…，um］T∈Rm，满足

式中，i=1，2，…，m；s（·）代表操纵面约束限制。则式（1）的二次规划问题的解满足以下不动点等式:

这样，可得到不动点迭代格式为:

1.2 MDD不动点迭代方法

MDD不动点法的基本思想是对一组迭代点沿其中的最大梯度下降方向进行修正，以加快迭代的收敛速度。

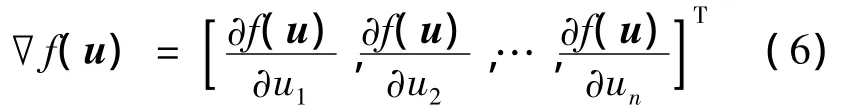
定义 2:对于u0∈Rn，d∈Rn，函数f在点u0关于方向d的方向导数定义为:

用Df（u0；d）表示f在点u0关于方向d的方向导数。当f的一阶偏导数连续可微时，方向导数可用下式计算:

由上面的定义可得，用于不动点迭代的f（u）在u点的梯度定义为:

式中，等式左侧左上角的f表示不动点迭代；Δt为迭代步数的间隔，一般取为1。因此，f在迭代点u0关于方向d的方向导数可用下式计算:

因此，MDD即为

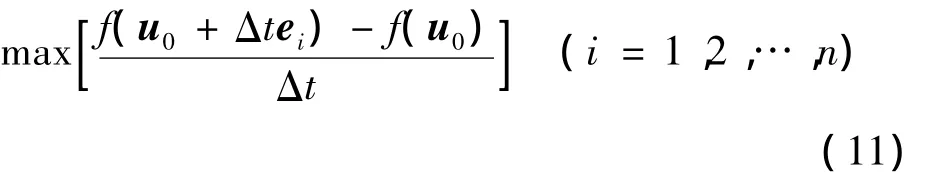
所对应的单位方向ei。

定义3:对于uk，uk+1∈Rn和单位向量ei，函数f在点uk+1关于方向ei的增量定义为:

在MDD不动点迭代算法中，将当前迭代点及其前一个迭代点在MDD上的迭代增量作最小二乘拟合，得到下一迭代点在该MDD上的估计迭代增量作为当前迭代点的更新迭代增量。那么，对于MDD不动点迭代（k≥1，k∈N），其算法步骤如下:

（1）取f（uk），f（uk+1）；

（3）计算 Δf（uk+1；em），Δf（uk；em）（k≥2，k∈N）并进行最小二乘拟合，得到当前迭代点uk+1估计的下一迭代点在em方向上的迭代增量Δ*f（uk+1；em）；

（4）更新f（uk+1）=f（uk+1）+Δ*f（uk+1；em）em；

（5）以uk+2=f（uk+1）作为新的迭代点，计算f（uk+2），f（uk+3）；

（6）若满足k＜K（K∈N）且‖▽ff（uk+1）‖ ＞ξ（ξ＞0），重复步骤（1）～ （5）；否则，转为基本不动点迭代算法。

需要注意，对于存在约束条件的控制分配问题，步骤（4）更新的f（uk+1）还应满足其约束条件。

1.3 混合MDD不动点迭代方法

由于伪逆法具有计算量小和易于实现等优点。但是，其并没有直接考虑到操纵面的饱和（位置和速率）约束限制，不能避免操纵面进入饱和。因此，考虑将伪逆法和MDD不动点法结合，在求解控制分配问题时，先用伪逆法求解，若结果在约束限制内，则采用伪逆法结果；若结果超出约束限制，则用MDD不动点法求解，这种混合MDD不动点迭代方法兼顾了两种方法的优点。

1.4 混合MDD不动点迭代方法的收敛性

在讨论混合MDD不动点迭代法的收敛性之前，先讨论基本不动点迭代法的收敛性［7］。将控制分配问题变为标准的二次规划问题，如下:

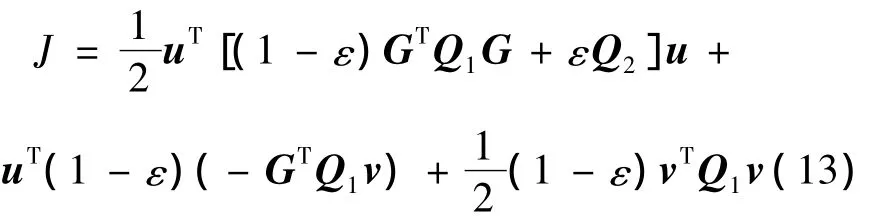
当代价函数为凸函数时，任意优化算法都应满足库恩-塔克（Kuhn－Tucker）［8］条件，基于二次规划的优化算法也不例外。对于凸规划，库恩-塔克条件既是必要条件，也是充分条件。点u*是正定二次规划问题的全局最优解的充要条件为u*为 Kuhn－Tucker点［8］。由文献［9］可知，不动点等式（4）的解也是二次规划问题（14）的唯一解，从而可以得出不动点迭代法可以精确求解二次规划问题［10］。这也就说明了基本不动点迭代法的收敛性。

由此，设u*是该二次规划控制分配问题的全局最优解。设基本不动点的迭代序列为{un}，则该数列收敛于u*。由上文给出的MDD不动点迭代设计步骤可知，该算法仅改变了不动点迭代序列{un}的有限项，因此不影响该序列的收敛性。进一步，由数列极限的唯一性可知，MDD不动点迭代序列也收敛于u*。由此，易知混合MDD不动点迭代序列也是收敛的。

2 仿真实例及分析

2.1 混合MDD不动点法的正常控制分配

采用ADMIRE模型进行仿真，仿真中所用主要数据如下:

操纵面定义如下:

其饱和约束限制如表1所示。

表1 操纵面的位置限制与速率限制

仿真中，在0.5 s输入两组虚拟阶跃信号V1和V2。对两组输入信号进行基于伪逆法（PINV）、内点法（Interior Point，IP）、不动点（FXP）方法和混合MDDFXP方法的控制分配对比，每种方法各进行100次仿真，其各自平均运行时间如表2所示。

表2 不同方法的平均运行时间对比 （s）

从表2中可知，在两组仿真中，混合MDDFXP均是除PINV方法外运行时间最少的方法，并且PINV方法的运行时间相比混合MDDFXP方法并没有绝对的优势。此外，在两组仿真中，混合MDDFXP方法比FXP方法分别提高了12.46%和5.35%。限于篇幅，仅给出了V2输入下的对比图（见图1），并且由于混合MDDFXP方法与FXP方法在分配输出上是一样的，所以仅给出了混合MDDFXP方法与其他方法的对比输出。

图1 V2输入下不同控制分配方法的对比

由图1可知，对于第2组虚拟输入，混合MDDFXP方法的控制分配效果完全达到了期望的输入；并且在PINV方法的控制分配输出中，v1，v2和v3均存在着明显的稳态误差；尤其是PINV方法没有考虑操纵面的饱和约束限制的致命缺点，更将限制其应用；此外，IP方法对于v1，v3的分配结果也存在些较小的稳态误差。

以上分析说明了混合MDDFXP方法在控制分配中的可行性，相比基本FXP方法具有快速性。

2.2 基于混合MDD不动点法的故障重构控制

上文中已验证了混合MDD不动点方法在正常控制分配问题中的有效性和快速性。下面，进一步研究该方法在多操纵面飞机故障情况下的重构控制分配效果。沿用文献［11］中故障时的分配器设计，对右外升降副翼损伤50%的故障进行重构控制分配，在2 s设置相应故障，并在2.5 s进行重构，其仿真曲线如图2所示。

图2 右外升降副翼损伤50%重构前后仿真图

由图2可以看出，重构后的其他正常操纵面很好地补偿了损伤的故障操纵面对输出信号的影响，获得了良好的控制分配效果，而且在1 s之内重构输出即可跟踪上正常输出，这说明了该方法在重构控制分配中的有效性和快速性。

3 结束语

本文研究了一种基于改进不动点迭代的容错控制分配方法，结合了伪逆法和MDD不动点法的优点，并应用于多操纵面飞机的重构控制分配。在正常和故障重构控制分配中，算法不仅考虑了操纵面的饱和约束限制，并且在运行时间上比基本的不动点算法更快速，适合应用于多操纵面飞机的故障重构控制分配。MDDFXP方法步骤（6）中的跳出条件对迭代速度的影响情况是进一步的研究方向。

［1］史静平，章卫国，李广文，等.再分配伪逆算法分配效率研究［J］.中国科学（信息科学），2010，40（4）:519－525.

［2］Oppenheimer M W，Doman D B，Bolender M A.Control allocation for over－actuated systems［C］//14th Mediterranean Conference on Control and Automation.Ancona，Italy，2006:1－6.

［3］Härkegård O.Backstepping and control allocation with applications to flight control［D］.Paris:Linköping University，2003.

［4］Schofield B，Hägglund T.Optimal control allocation in vehicle dynamics control for rollover mitigation［C］//American Control Conference.Washington，USA，2008:3231－3236.

［5］Johansen T A，Fuglseth T P，Tondel P，et al.Optimal constrained control allocation in marine surface vessels with rudders［J］.Control Engineering Practice，2008，（16）:457－464.

［6］Burken J J，Lu P，Wu Z，et al.Two reconfigurable flightcontrol design methods:robust servomechanism and control allocation［J］.Journal of Guidance，Control，and Dynamics，2001，24（3）:482－493.

［7］曲小宇，章卫国，严谨，等.不动点法在飞控系统控制分配中的应用［J］.计算机仿真，2009，26（9）:66－69.

［8］黄红选，韩继业.数学规划［M］.北京:清华大学出版社，2006.

［9］Wang J，Longoria R G.Coordinated and reconfigurable vehicle dynamics control［J］.IEEE Transactions on Control Systems Technology，2009，17（3）:723－732.

［10］Lu P.Constrained tracking control of nonlinear systems［J］.Systems and Control Letters，1996，27（5）:305－314.

［11］崔玉伟，章卫国，李广文，等.基于线性规划的多操纵面重构控制研究［J］.飞行力学，2011，29（2）:41－44.