基于传声器阵列网络的改进高斯粒子跟踪算法*
2012-07-25江潇潇杨旭光赵鲁阳王营冠
江潇潇,杨旭光,赵鲁阳,王营冠
(中国科学院上海微系统与信息技术研究所无线传感器网络与通信重点实验室,上海 200050)
0 引言
目标跟踪一直是军事和民用领域共同关注的一个基本问题,随着现代信息化、网络化的迅速发展,传声器阵列网络由于其隐蔽性好、能耗低、不受光照条件影响等优点成为新的研究热点,有着十分广阔的应用前景。基于声阵列网络的目标跟踪是通过目标发出的声波信号的方位角测量序列估计当前目标的运动状态参数,因此基于声阵列的纯方位跟踪是一个典型的非线性滤波问题。针对非线性问题常用的滤波算法有扩展卡尔曼滤波(extended Kalman filter,EKF)[1]算法,无味卡尔曼滤波(unscented Kalman filter,UKF)[2]算法,粒子滤波(particle filter,PF)[3]算法等。EKF在遇到强非线性问题时精度会严重降低,滤波容易发散,UKF虽然克服了EKF的缺点,在非线性系统中滤波性能优于EKF[4],但却大大增加了运算量,且对观测数据的依赖性较强,容易受到干扰。PF适用于任何非线性非高斯噪声环境,精度较EKF,UKF高,当粒子数趋于无穷时,粒子滤波可达到最优贝叶斯估计。
粒子滤波通过一个蒙特—卡罗过程来完成贝叶斯滤波[5],其基本思想是用一系列随机采样点即粒子来近似状态向量的后验概率密度,以样本均值代替贝叶斯滤波的积分计算从而获得状态估计值。然而PF存在粒子退化问题,虽然重采样技术[6]通过对大权值粒子的复制和分裂以及小权值粒子的剔除可以部分解决退化问题,但同时也带来了粒子耗尽问题等。人们提出了很多关于PF的改进算法,其中扩展卡尔曼粒子滤波(EPF)[7,8]利用当前时刻的量测来提高对后验概率密度函数估计的精度,UKF[9]引入UT(unscented transformation)变换来获得后验概率密度函数的分布,这些算法在提高PF精度的同时却带来了计算量的增加。文献[10]提出了高斯粒子滤波(GPF)算法,相比PF,不需要重采样,不存在粒子退化现象,极大地降低了PF的复杂性和计算量,并且同样适用于非线性非高斯环境。
本文首先建立了传声器阵列网络的跟踪系统模型,接着阐述了GPF的基本原理,针对GPF算法的特点,结合EKF的状态更新算法,对传统的GPF算法进行了改进,并给出了改进的GPF算法流程,最后对算法进行了仿真验证,并与EPF算法与传统的GPF算法进行了比较。
1 基于声阵列网络的目标跟踪模型
1.1 模型描述
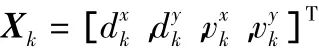
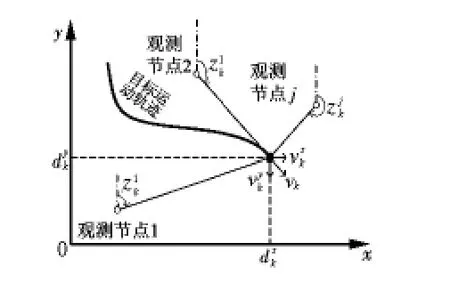
图1 基于声阵列网络的目标跟踪模型Fig 1 Target tracking model based on microphone array networks
1.2 系统状态方程
本文目标的运动模型选择最有普遍意义的恒速模型[11]。假设目标做匀速直线运动,并加入随机的高斯白噪声加速度,可建立离散系统状态方程

式中F和B分别为状态转移矩阵和噪声分布矩阵,Wk为过程噪声,具体表示为
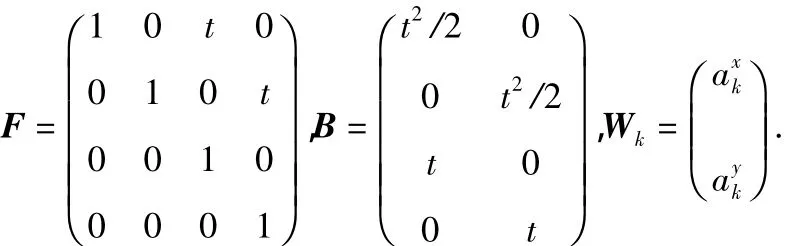
1.3 声阵列量测方程
根据二维几何平面关系,可以得到k时刻声阵列网络的量测方程

式中函数矢量为

表示传感器节点观测值与节点坐标及目标坐标值之间的函数关系,其具体函数形式为
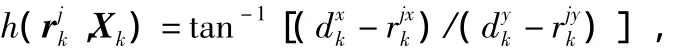
2 GPF及其改进算法设计
GPF采用PF方法确定高斯密度函数,其基本思想是利用重要性采样对状态变量进行后验期望和方差的近似,通过高斯概率密度对非线性系统的滤波概率密度和预测概率密度进行近似。GPF算法只给出了滤波的基本框架,具体实现方法很多。本文在PF算法的基础上,提出了一种新的改进算法,在一定程度上提升了滤波精度和算法的稳定性,在声阵列网络目标跟踪中具有一定的应用价值。
2.1 GPF
GPF是通过粒子滤波方法得到一个高斯分布来近似被估状态量的后验概率分布,具体来说是假设系统在k时刻的后验概率密度函数和k+1时刻的先验概率密度函数为高斯分布,然后对该高斯分布进行抽样。通过对高斯密度函数的采样得到粒子集,从而避免了粒子枯竭,省去了重采样步骤。GPF分为2个阶段:测量更新和时间更新。
1)测量更新
当获得k时刻节点观测量Zk时,高斯粒子滤波可由式(3)表示

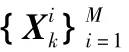
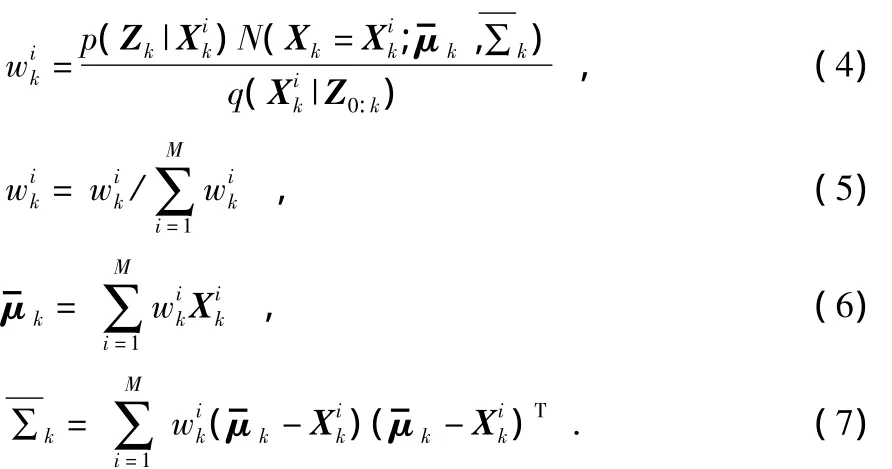
2)时间更新

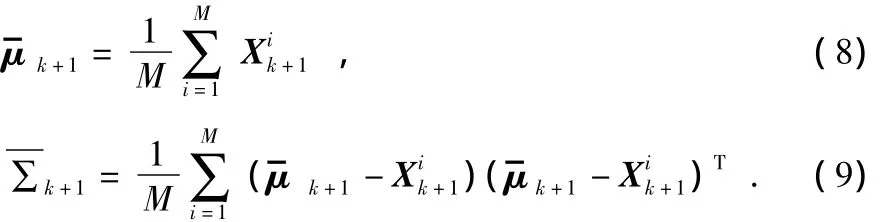
文献[10]同时给出了另一种统计方法,本文采用第二种统计方法进行时间更新

2.2 改进GPF算法
在传统的GPF过程中,粒子的状态更新是通过状态方程和噪声分布对粒子集中的每个粒子逐个进行更新,而且没有充分考虑每个采样时刻量测对状态估计的影响,在一定程度上降低了状态估计的精度,计算量也比较大。本文基于上述观点,提出了一种基于声阵列网络目标跟踪应用的改进GPF算法,一方面,该算法通过利用EKF的状态更新方法取代GPF中的状态更新过程,从而考虑了量测值对状态估计的影响,提高了滤波精度。另一方面,该算法在状态更新过程中,直接更新状态量的高斯分布参数即均值和方差,而不是对每个粒子逐个更新,在很大程度上减低了运算量。下面给出算法的具体实现步骤:
1)对粒子集初始化:假设目标初始状态分布p(X0)已知,采样粒子~p(X0),对应的权值按式(4)计算;
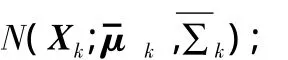

状态预测

状态更新
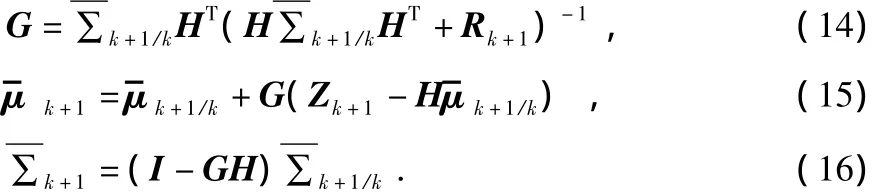


5)返回第2步,循环以上步骤。
改进的GPF算法的实现过程是首先初始化粒子集,再计算GPF粒子高斯分布参数即均值和协方差;其次在粒子的更新过程中,不直接更新粒子,而更新粒子的高斯分布参数,更新方法借鉴EKF算法。粒子更新充分考虑当前时刻的量测,使粒子的分布更加接近状态的后验概率分布。算法选取重要性密度函数为其先验分布密度函数,从而使GPF进一步简化。
3 仿真结果与分析
为了验证模型和本文提出改进算法的有效性,在MatlabR2008a环境下对其进行仿真,并与EPF,GPF算法进行比较。假设声阵列网络中有5个观测节点,它们在坐标系中的位置分别是[5,5 m],[200,5 m],[200,200 m],[5,200 m],[100,100 m],目标的初始位置为[10,20 m],目标的初始速度为[5,5 m/s]。通过系统输入加速度噪声来改变目标运动状态,设x轴和y轴的加速度为方差1m/s2的白噪声。取节点观测噪声的方差为3°,设观测周期为1 s。图2所示为一次观测过程中某一传感器节点测量值与目标真实位置对比结果,从图中可以看出传感器节点受噪声的影响,观测值与真实值之间有很大的误差。
采用粒子数M=100,蒙特—卡罗仿真次数Nmc=100,在上述参数设置下进行了仿真。图3是目标运动轨迹曲线和利用EPF,GPF以及本文改进GPF算法的滤波结果。
图4、图5是相应的轨迹上跟踪估计的位置均方根误差和速度均方根误差。
表1给出了EPF,GPF以及本文改进算法的均方根误差(RMSE)。

图2 传感器节点观测值与真实值比较Fig 2 Comparison of observations and real values of sensor node
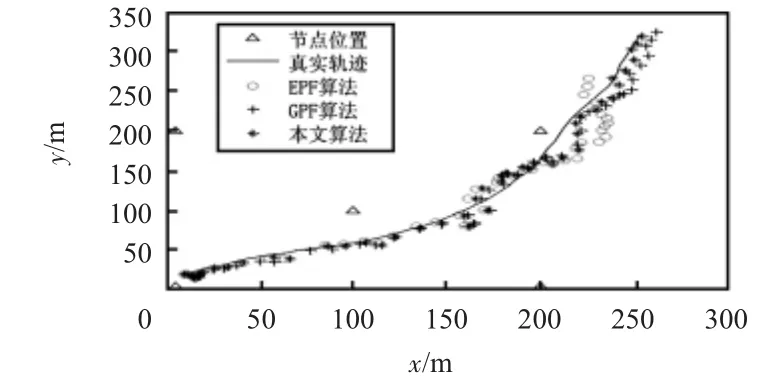
图3 目标轨迹跟踪结果Fig 3 Tracking results of the target
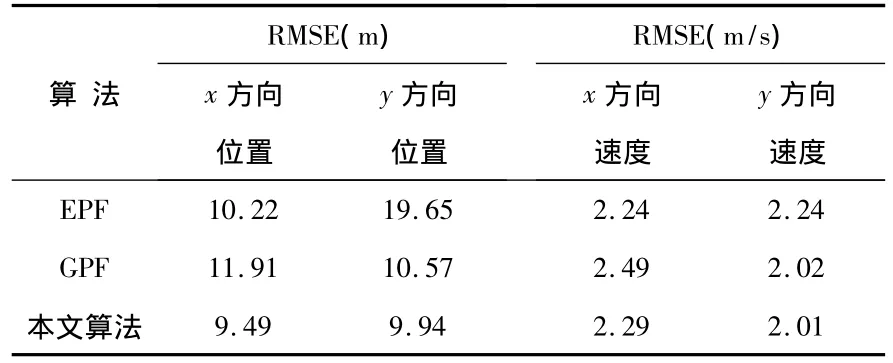
表1 几种算法的平均RMSE比较Tab 1 Mean RMSE comparison of different algorithms
从仿真结果可以看出:在跟踪的最初阶段3种算法的误差都比较大,根据分析,这可能是由于初始化参数的设置和目标运动模型不完全匹配所造成的。在第7 s之后,三种算法的跟踪精度开始提高,从图4~图5中可以看出:本文提出的改进算法比传统的GPF收敛速度更快。在第13~35 s的阶段,3种算法精度相差不多,x轴与y轴误差基本能够保持在10 m以下。从第35 s开始,EPF算法精度下降,误差累积增大,而GPF和改进后的GPF精度相对比较稳定,并且改进后的GPF算法因为考虑到了新的量测对状态估计的影响,跟踪结果更加逼近目标的真实轨迹。从表1也可以看出:在算法的平均性能上,本文提出的算法在位置估计上的误差减小了很多,并且在跟踪图上也可以看出:本文算法在长时间跟踪中表现得更为可靠。
4 结束语
本文对基于声阵列网络的目标跟踪问题进行了系统建模,提出了一种改进的GPF算法,在传统GPF算法的基础上,用EKF的方法取代GPF中粒子状态更新的方法,在对状态量的估计中考虑到了新量测值的影响,并用直接更新状态量的高斯分布参数的措施降低计算量。最后结合声阵列的目标跟踪模型进行仿真验证,并与EPF,GPF算法进行了对比,仿真结果表明:改进后的算法在精度和稳定性上有所改善。

图4 目标位置估计均方根误差Fig 4 RMSE of the target position
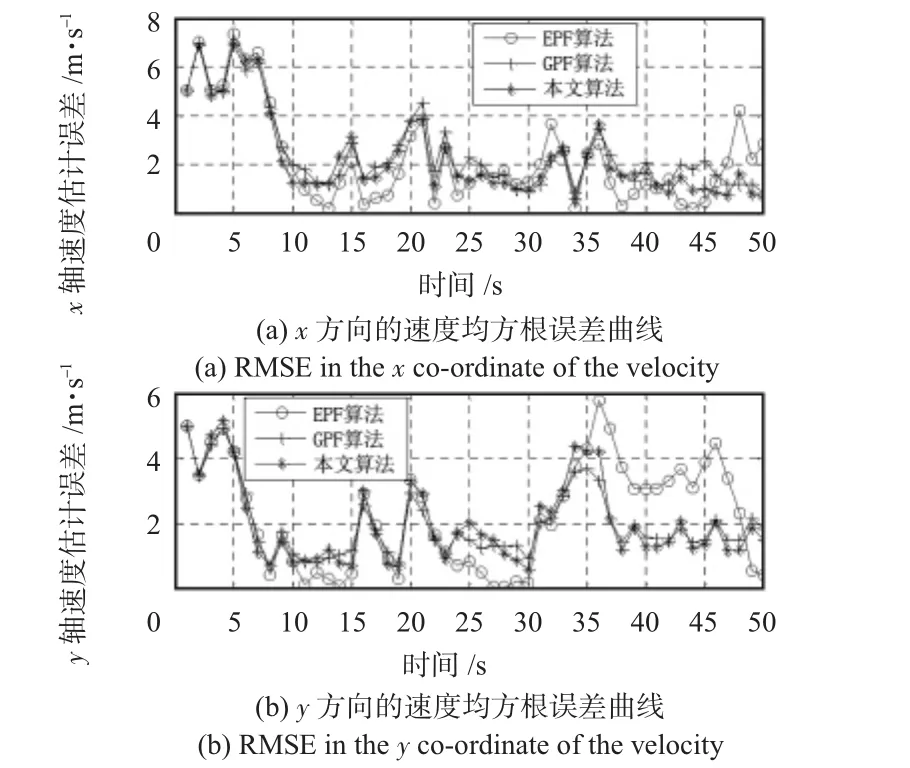
图5 目标速度估计均方根误差Fig 5 RMSE of the target velocity estimation
[1]Bar-Shalom Y.Estimation and tracking-principles,techniques,and software[M].Boston,London:Artech House,1993:382 -410.
[2]Julier S J,Uhlmann J K.Unscented filtering and nonlinear estimation[J].Proceedings of IEEE,2004,92(3):1015 -1022.
[3]Gordon N J,Salmond D J,Smith A F M.Novel approach to nonlinear/non-Gaussian Bayesian state estimation[J].Radar and Signal Processing,1993,140(6):107 -113.
[4]Laneuville D,Jauffret C.Recursive bearings-only TMA via unscented Kalman filter:Cartesianvsmodified polar coordinates[C]//2008 Aerospace Conference,IEEE,Toulon,DCNS,2008:1 -11.
[5]Harrison P J,Stevens C F.Bayesian forecasting[J].Journal of the Royal Statistical Society,1976,3:205 -247.
[6]Arulampalam M S,Maskell S,Gordon N,et al.A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking[J].IEEE Trans on Signal Processing,2002,50(2):174 -188.
[7]Doucet A,Godsill S,Andrieu C.On sequential Monte Carlo sampling methods for Bayesian filtering[J].Statistics and Computing,2000,10(3):197 -208.
[8]王 彪,曾庆军,解志斌,等.基于水声传感器网络的目标纯方位运动分析[J].中国造船,2011,52(1):90 -96.
[9]Merwe R V,Doucet A,Freitas N D et al.The unscented particle filter[R].Beaverton:Oregon Graduate Institute,2001.
[10]Kotecha J H,Djuric P M.Gaussian particle filtering[J].IEEE Tran on Signal Processing,2003,51(10):2592 -2601.
[11]Singer R A.Estimating optimal tracking filter performance for manned maneuvering targets[J].IEEE Tans on Aerospace and Electronic Systems,1970,6(4):473 -483.
