舰载武器惯导系统传递对准仿真验证的研究*

赵 琳，荣文婷

（哈尔滨工程大学自动化学院，黑龙江哈尔滨 150001）

0 引言

传递对准利用舰船、飞机惯导系统（主惯导）的高精度导航信息，通过与武器系统惯导系统（子惯导）导航参数的有效匹配，估计出子惯导相对主惯导的失准角，能快速完成子惯导系统的初始对准，因此，在武器系统初始对准中得到大量的应用，具有非常广泛的应用发展前景［1，2］。在传递对准仿真研究和方案验证过程中，采用实物、物理仿真具有成本高、工艺要求复杂的缺点，特别是其不可重复性，制约了其使用范围。所以，普遍采用计算机仿真的方法对传递对准方案进行仿真验证［3］。

对于舰载武器系统传递对准仿真，传统的方法在设定载体运动时，只考虑给定运载体的有规律性的摇摆运动和理想的线运动［4，5］。而在自身操纵信息和海洋环境干扰因素的影响下，舰船的空间运动比理想设定值要复杂的多［6］。因此，本文提出了引入舰船空间运动模型实现舰载武器惯导传递对准算法考核的仿真验证系统，通过模拟接近真实的舰船运动环境，对传递对准算法的有效性、实用性进行验证。

1 传递对准仿真验证系统总体设计

针对传递对准算法研究及算法仿真验证的需求，仿真验证系统总体设计方案如图1所示。整个系统由以下三部分组成:

1）舰船空间运动模型:在给定初始条件和海洋环境干扰因素后，通过平动、转动及辅助方程解算，输出舰船相对动坐标系的速度、角速度及姿态信息。

2）传递对准基准与量测信息计算模型:接收舰船空间运动信息后，完成线运动和角运动信息计算、主惯导导航解算，结合杆臂、安装误差及挠曲参数计算子惯导的惯性敏感信息。

3）子惯导传递对准算法模块接收主惯导的基准信息和自身的惯性敏感信息，完成姿态最优估计，并与主惯导信息比较，完成对准误差计算。

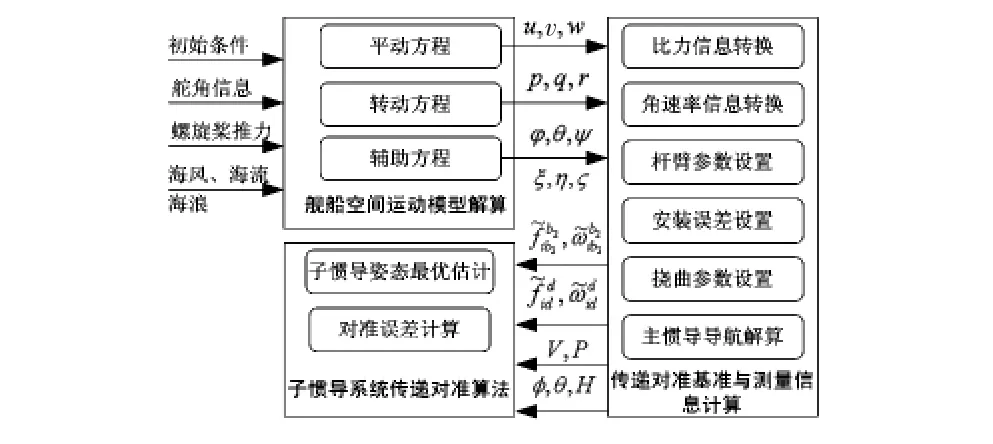
图1 传递对准仿真验证系统总体设计Fig 1 Overall design of simulation and verification system for transfer alignment

2 舰船空间运动模型建立和简化

2.1 舰船空间运动建模

利用刚体的动量定理和动量矩定理，根据牛顿运动定律与流体力学原理对舰船空间运动进行受力与力矩分析，建立舰船空间六自由度运动标准方程。在不影响舰船空间主要运动特性的情况下，建立其空间运动标准方程为［7］

式中u，v，w分别为舰船相对地球的速度在动系G－xyz纵向、横向和垂向分量;p，q，r为舰船旋转角速率在动系纵向、横向和垂向分量;fX，fY，fZ为舰船所受外力在动系轴向分量;fK，fM，fN为舰船所受外力矩在动系轴向分量;A=［aij］6×6为系数矩阵。

结合舰船空间运动辅助方程［7］，便能完成舰船空间线运动和角运动信息的实时解算。

2.2 海洋环境力建模

舰船在实际航行过程中，不仅存在受自身操控信息进行主动运动，而且不可避免会存在受海风、海浪、海流等海洋环境因素作用的被动运动。因此，需建立受海风、海浪、海流作用的舰船空间运动模型。

海风对水面舰船的影响使艇体x轴和y轴受到风力的作用，z轴则受到力矩作用［8，9］，即

式中XWIND为艇体x向所受风力，YWIND为艇体y向所受风力，NWIND为艇体z轴所受力矩;ρW为空气密度;Af为艇体水线上正投影面积;As为艇体水线上侧投影面积;L为艇体总长度;VW为相对风速;CXW，CYW，CNW，为风压力系数。

定常流对水面舰船的影响是使艇体x轴和y轴受到海流力的作用，z轴则受到力矩作用［8］，即

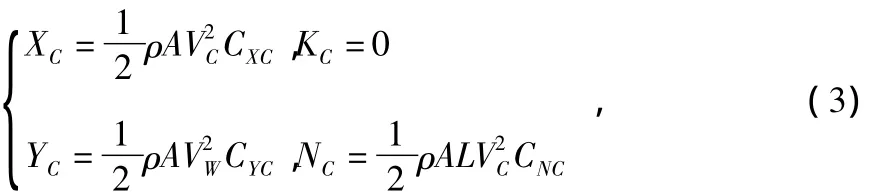
式中XC为艇体x向所受风力，YC为艇体y向所受风力，NC为艇体z轴所受力矩;A为水线长与吃水的乘积;VC为海流流速;CXC，CYC，CNC为海流力系数和海流力矩系数。

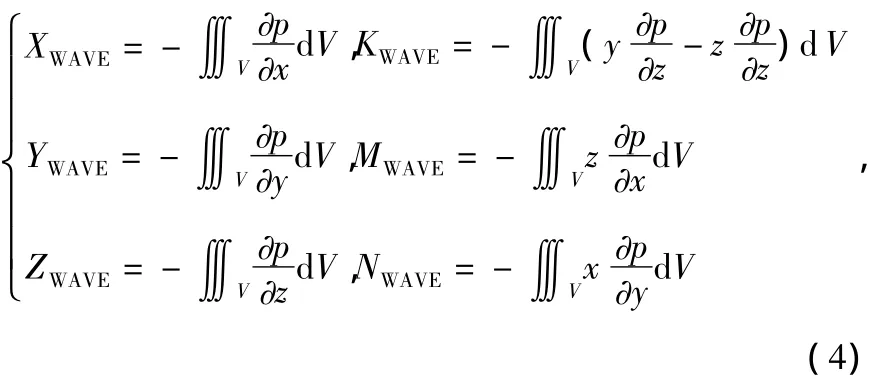
式中XWAVE，YWAVE，ZWAVE分别为艇体x，y，z向所受海浪干扰力，KWAVE，MWAVE，NWAVE分别为艇体x，y，z向所受海浪干扰力矩。

通过舰船空间运动方程和辅助方程的求解，能够解出舰船相对定坐标系的线运动参数u，v，w、角运动参数p，q，r、首向角Ψ、纵倾角θ和横倾角φ，从而模拟出接近实际的舰船运动状态。

3 主子惯导的惯性敏感信息转换

由于舰船的空间运动信息是沿动系各轴向，而捷联式惯导系统的输入是沿载体坐标系，且输入信息是相对惯性空间，因此，必须建立合理的空间坐标变换关系，才能实现舰船空间解算输出与惯导系统输入信息实现衔接。

3.1 空间运动信息至角速率信息的转化

定义空间信息转换所必需的坐标系:定系E（Eξηζ），动系b1（oxb1yb1zb1）选择国际水池会议推荐的和造船和轮机工程学会公报的体系，且设定系Eξ轴与地理系北向夹角为α。地理系t（oxtytzt）、载体系b2（oxb2yb2zb2）如图2所示。

图2 空间坐标系示意图Fig 2 Diagram of space coordinate system

根据图2所示E系与t系的关系可知，从定系绕Oζ轴旋转－（90°+α）得到E1，再绕Oη轴旋转180°即得t系，二者的坐标变换矩阵可描述为

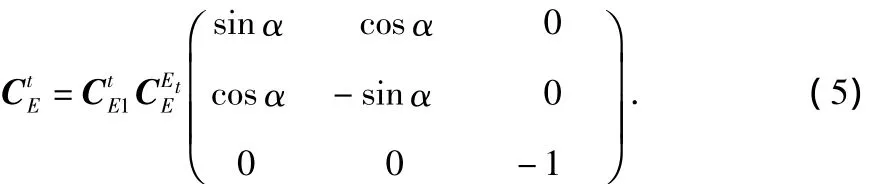
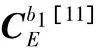
根据图2所示，b1系绕轴旋转180°，再绕z'轴旋转－90°，可得载体系b2。由此得到b1系与b2系的坐标旋转矩阵为

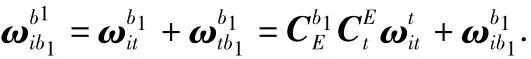
由于定系E相对地理系t无转动，有=0，即

由直角坐标变换的正交性特性，=［］T，根据式（5）、式（6）及式（7），可以得到

由于b1系与b2系无相对转动，即=0。由此，根据式（7）、式（9）可以得到沿载体系，相对惯性空间的旋转角速率为

在考虑陀螺仪标度系数误差、安装误差与漂移误差的情况下，陀螺仪敏感的角速率输出为

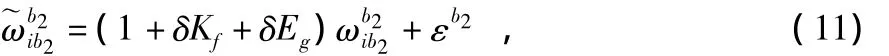
式中δKg，δEg分别为陀螺仪标度系数误差、安装误差与漂移误差。

3.2 空间运动信息至比力信息转化

由哥式定理可以得到运载体相对惯性系的比力信息ft与载体相对地球的运动加速度的关系为［10］

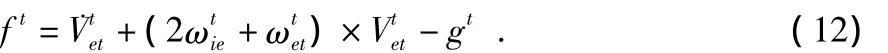
式中 载体相对地球的运动加速度可由沿动系的速度微分运算得到，即

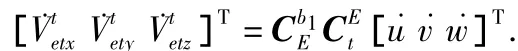
由此可以得到主惯导所在位置的比力信息为

在考虑加速度标度系数误差、安装误差和零偏误差的情况下，加速度计敏感的比力信息为

式中δKa，δEa，分别为加速度计标度系数误差、安装误差和零偏误差。

通过式（11），式（14）提供的主惯导角速率、比力信息，以及捷联式惯导系统的基本导航算法［11］，可以完成主惯导的导航定位参数解算，包括姿态、速度及位置信息。

3.3 子惯导敏感信息计算

设由子惯导惯性元件敏感轴构成的空间直角坐标系用d系描述，由于挠曲变形、安装失准角而产生的主、子惯导所在位置的角速率关系为［11］

式中为子惯导相对主惯导有 θ =［θθθ］T装角所形xyz成的坐标变换矩阵;为由于挠曲变形引起的角运动，采用二阶马尔科夫过程描述时［12］，有

式中βi=2.146/τi，τi为各个轴变形角的相关时间。

在考虑子惯导系统陀螺仪计标度系数误差、安装误差偏差与漂移偏差的情况下

受到杆臂效应、挠曲变形、安装失准角而产生的主、子惯导所在位置的比力信息关系为［10］

在考虑子惯导系统加速度计标度系数误差、安装误差偏差与漂移偏差的情况下

4 计算机仿真

采用“速度+姿态”传递对准方法设计子惯导系统的传递对准算法［11］。

1）惯性器件误差设定

陀螺常值漂移εx=εy=0.01°/h，随机漂移为 0.001°/h，陀螺刻度因数误差为10－4;

加速度计随机常值偏置为Δx= Δ

y=1×10－4g0（g0=9.78049 m/s2），随机误差为 10－5g0，刻度因数误差为 10－4。

2）卡尔曼滤波器初始状态设定

初始状态各变量均为零;初始方差P0

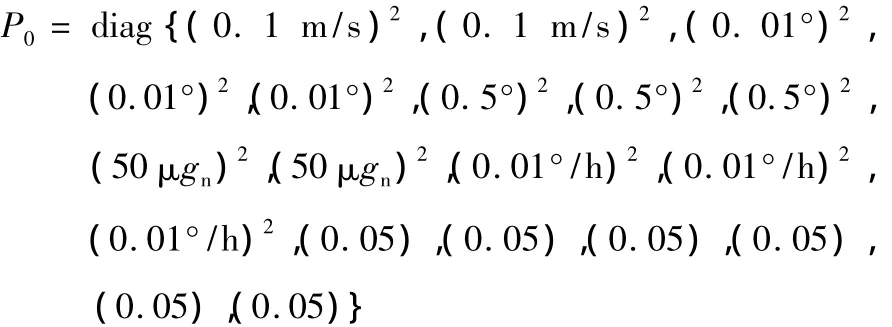
噪声Q

噪声R

3）子惯导相关参数设定:

杆臂效应参数rb2=［6 5 8］T;相关时间τi=2s;安装失准角 θ =［0.5°0.5°0.5°］T。

4）舰船运动状态设定

设定海浪波长λ=70 m，舵角信号及螺旋桨推力，使系统分别处于下述2种状态:1）v=5 kn的匀速直航状态;2）v=9 kn的匀速直航状态;

5）仿真结果

仿真结果如图3。由仿真结果可分析得出:

1）在给定舰船运动控制信息后，舰船空间运动模型解算和传递对准基准及测量信息模块能正确计算子惯导传递对准所需的基准观测信息和惯性敏感信息，实现子惯导姿态误差角的正确估算。

2）基于舰船空间运动的传递对准仿真验证系统通过“速度+姿态”很好地实现了安装失准角的快速有效估算。

3）通过挠曲变形角的估算值与理论值比较，证明该仿真验证系统正确估算出载体的挠曲变形角。

图3 仿真曲线Fig 3 Simulation curve

5 结论

通过建立考虑海洋环境力等干扰因素在内的舰船空间运动模型，设计空间运动至惯性敏感信息的空间变换算法，完成了舰载武器惯导传递对准仿真验证系统设计。该系统能为船用捷联式惯导系统传递对准方案验证提供接近实艇的仿真运动环境，仿真结果证明该算法的正确性。该算法不仅为船用惯导传递对准性能考核提供一种有效的考核方法，而且为其它类型载体的传递对准考核提供了参考。

［1］宫晓琳，房建成，郭 雷.SINS快速传递对准技术研究［J］.宇航学报，2008（4）:1228－1232.

［2］刘 毅，刘志俭.捷联式惯导系统传递对准技术研究现状与发展趋势［J］.航天控制，2004（5）:50－55.

［3］钱伟行，刘建业，赵 伟，等.平台式/捷联式惯导传递对准仿真平台的实现［J］.系统工程与电子技术，2007（5）:795－799.

［4］吴盘龙，陈 帅，薄煜明.精确制导炸弹传递对准仿真平台研究［J］.计算机仿真，2009（2）:79－83.

［5］王希彬，赵国荣，高青伟.舰载机惯导系统快速传递对准方法建模与仿真［J］.飞行力学，2009（2）:63－66.

［6］王新屏，张显库，关 巍.舵鳍联合非线性数学模型的建立及仿真［J］.中国航海，2009（4）:58－64.

［7］贾欣乐，杨盐生.船舶运动数学模型［M］.大连:大连海事大学出版社，1999:31 －46.

［8］姚云熙.水面无人艇在风浪流干扰下的运动仿真［D］.哈尔滨:哈尔滨工程大学，2001:23－27.

［9］王志东，杨松林，赵洪江.风、流作用下船舶操纵运动的模糊控制方法［J］.华东船舶工业学院学报，1999，13（1）:19 －22.

［10］李 璞.舰载武器惯导系统传递对准技术研究［D］.哈尔滨:哈尔滨工程大学，2006:53－62.

［11］滕英祥.船舶在风浪中的操纵运动仿真［D］.大连:大连海事大学，2004:36－39.

［12］Mochalov A V，Kazantsev A V.Use of the ring laser units for messurement of the moving object deformations［C］//Proceeding of SPIE，2002:85 －92.