异构无线传感器网络中多目标优化节点部署策略*

冀文娟，石为人，李 明，李 曼

（重庆大学自动化学院，重庆 400030）

0 引言

节点部署是无线传感器网络（wireless sensor networks，WSNs）的基本问题，决定了传感器监测物理空间的效果。覆盖反映网络所能提供的“感知”服务质量［1］，实现优化分配无线传感器网络的空间资源，进而更好地完成环境感知、信息获取和有效传输任务。因此，覆盖质量和能耗是无线传感器网络节点部署必须考虑的问题。

文献［2］提出一种基于遗传算法在保证充分覆盖的前提下，使得参与覆盖的节点数最小的最优覆盖方法。文献［3］以网络覆盖最大和传感器节点利用率最小为目标，提出基于二进制随机多目标粒子群优化算法。文献［4］以网络覆盖率为目标，提出基于改进蚁群算法的节点优化部署方法。文献［5］提出了基于概率测量模型的以网络覆盖率为目标的粒子群优化策略。上述研究均针对同构网络即参与覆盖的节点参数相同，并且大多采用二元感知模型，不能反映节点实际探测时的不确定性。同时研究没有考虑到事件发生呈现的“热点”区域。针对这些问题，本文提出一种基于二进制粒子群的以区域覆盖率最大和单位面积网络能耗最小为目标的多目标异构传感器网络节点部署策略。

1 问题描述

假设监测区域A为二维平面，A被离散化为N个栅格，单位栅格面积为1。有K种不同类型的传感器节点M个，其感知半径rk和通信半径rkc，且满足rkc≥2rk，保证异构节点部署后构成一个连通的网络。xik表示栅格i处的节点放置情况

1.1 异构网络覆盖模型与覆盖率

类型为k的传感器节点sik的位置为（xik，yik），对于任意格点q（xj，yj），传感器节点与栅格点间的欧氏距离为

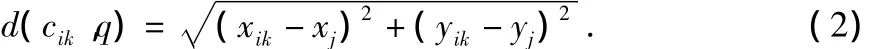
点q被i所覆盖的事件定义为rijk，该事件发生的概率为p（rijk）。现有研究多数采用简单的二元感知模型，即

然而，在实际应用中，由于监测环境和噪声干扰和信号强度随传输距离的衰减，传感器节点的感知能力具有不确定性，因此，本文采用概率感知模型［6］

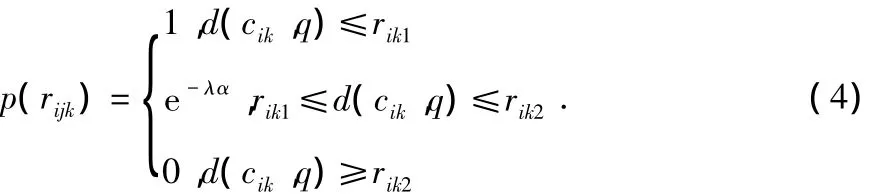
其中，α=d（cik，q）－rik1，λ为与监测概率有关的参数，rik1，rik2分别为k型传感器节点的内外感知半径。假设监测区域内rijk的发生具独立性，定义任意格点q被区域内放置的传感器节点感知的事件为rj，该事件发生的概率p（rj）为

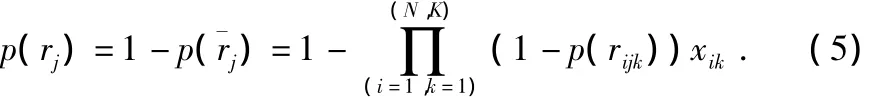
根据覆盖要求，用pthj表示格点p的覆盖概率门限值，用c（pj）表示格点p是否满足覆盖要求

网络中区域覆盖率P定义为

1.2 异构网络能耗模型

根据能量消耗模型［7］，单个k型节点在网络覆盖中的能量消耗为

其中，rk为k型传感器节点的感知半径。节点部署后，监测区域单位面积的能耗为

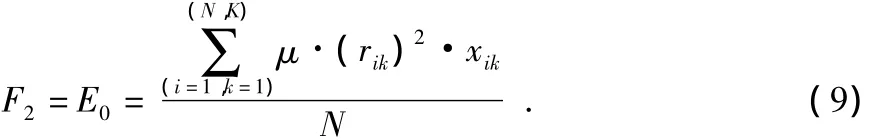
1.3 覆盖优化目标

异构无线传感器网络节点部署优化目标是:网络区域覆盖率最大和网络能耗最小。即要同时考察2个目标:网络区域覆盖率函数和监测区域单位面积能耗函数。这是一个多目标优化，问题可表达为

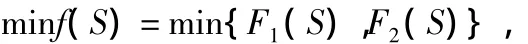
与单目标优化问题不同，求解多目标优化问题时，不是只有一个最优解而是要寻求一个非劣最优解集合。

2 节点部署策略设计

2.1 多目标优化的二进制粒子群算法原理

粒子群（particle swarm optimization，PSO）算法是一种通过模拟鸟群捕食行为的群智能算法，具有速度快、解质量高、鲁棒性好等特点［8］。为解决工程实际中的组合优化问题，Kennedy和Eberhart于1997年首次提出二进制PSO，它将每个位置分量xij限制在集合{1，0}中，而速度vij不做这种限制。在更新粒子位置时，vij越大，粒子位置xij取1的概率越大。粒子速度和位置更新公式为

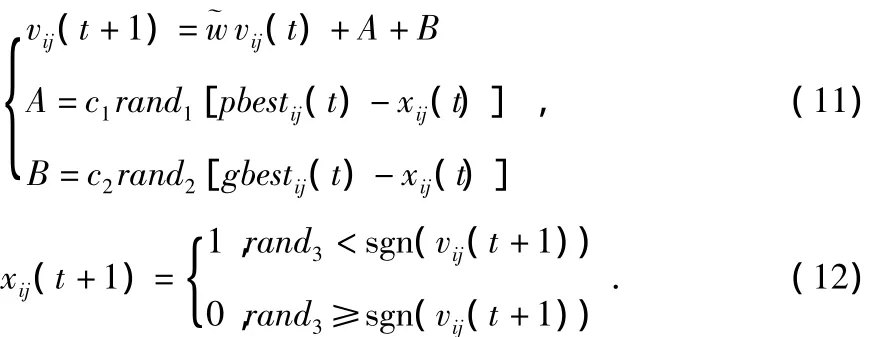
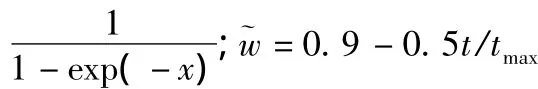
多目标优化的二进制粒子群算法（multi-objective binary particle swarm optimization，MOBPSO）中支配关系定义:1）任意2个粒子x1，x2，对于∀fi都有f1（x1）≤fi（x2），∃fi存在目标函数fj使得fi（xi）＜fi（x2），则称粒子x1支配x2。2）对于不满足上述关系的任意x1，x2，对于∀fi，都有|fi（x1）＜fi（x2）|≤εm，∃fi使得|fi（x1）＜fi（x2）|εm，则随机选取x1或x2，如果选中x1，则称粒子x1支配x2。引入强支配系数C［9］

使粒子间保持一定的距离，使非劣解均匀分布，防止粒子群早熟。

基于Pareto支配关系的最优解选择排序方法:在粒子群中选取一个粒子xi与剩余粒子依次比较，通过粒子群中剩余粒子与xi的关系，将种群分为两部分，A部分为支配xi和与xi不相关的粒子，B部分为被xi支配的粒子。若xi不被任何粒子支配，则将xi存入存放Pareto解集的EXS中。然后对A部分的粒子重复上述过程，直到将A部分粒子清空。

适应度函数:采用自适应加权适应度分配［10］，求解目标空间中各粒子的各目标函数值，通过比较得到各目标函数的权重值为

则粒子的适应度值为

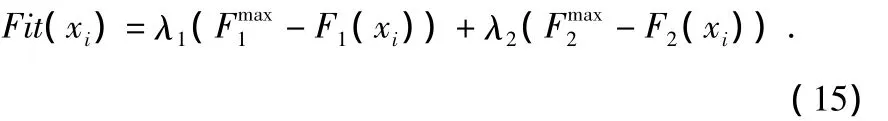
通过适应度值可区分Pareto解集。

pbesti（t）和gbesti（t）的取值:在EXS中的Pareto解集中随机选取2个解比较其适应度值，进而选取较优的解作为pbesti（t）或gbesti（t）。

算法约束条件:各类型传感器节点不超过给定的数量。若当前粒子不满足约束条件，则该粒子删除，重新随机产生一个新粒子，增加粒子群的多样性。

2.2 算法实现步骤

1）编码机制:粒子群中任意粒子Xi的维数为Q，Q=［log2K］+1，［X］为取整运算，K为传感器类型数，编码机制如图1所示。

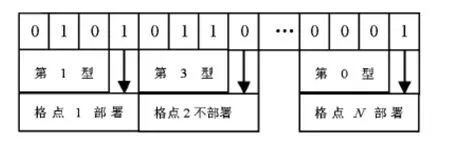
图1 粒子编码机制示意图Fig 1 Schematic diagram of particle encoding mechanism

2）初始化粒子群规模PS，外部存储空间EXS，粒子初始位置Xi（0）、初始速度υi（0）、迭代代数t=0。初始化算法参数:w，c1，c2。判断初始化后的粒子群是否满足约束条件，若否则重新生成粒子群。

3）计算各粒子的目标函数值:通过粒子间的支配关系排序，将非支配关系的粒子位置存入EXS。

4）更新粒子速度和位置信息:更新后的粒子若不满足约束条件，则将该粒子删除，重新随机产生一个。

5）更新Pareto解集:如果Pareto解集中某个粒子与新存入的粒子存在支配，则从EXS中将被支配的粒子删除。

6）判断算法是否达到最大迭代次数，是则退出，否则，转向步骤（3）。

3 仿真与结果分析

假设在40 m×40 m的监测区域中，不同区域覆盖要求不同，即会出现监测目标数量多、密度大的“热点区域”，该区域对网络的覆盖要求相应较大。如图2所示为区域监测覆盖率要求示意图，不同的区域覆盖率对应不同颜色。其中包括对覆盖要求较高的深色“热点区域”和对覆盖要求相对较低的浅色区域。

仿真系统中传感器类型和相关参数如表1所示。

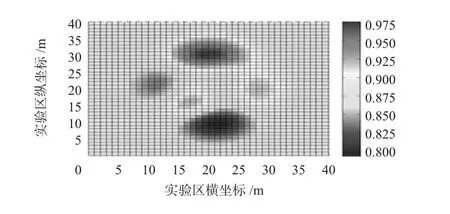
图2 监测区域覆盖要求示意图Fig 2 Schematic diagram of monitoring regional coverage requirements

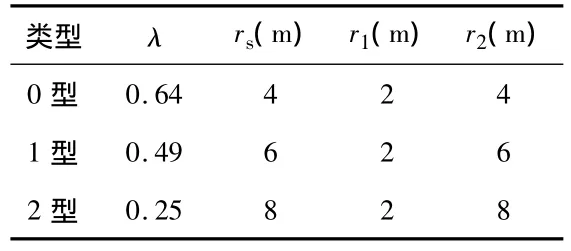
表1 传感器类型参数表Tab 1 List of sensor type parameter

能量参数μ=1，监测区域中各栅格覆盖率阈值根据监测要求生成。图3为本文算法运行结束后的到的Pareto解集中适应度值最大的解，其中用星号、圆圈、五角星分别表示0，1，2型传感器节点。由于存在边界效应，导致除“热点区域”外，监测区域边缘传感器节点分布较多。

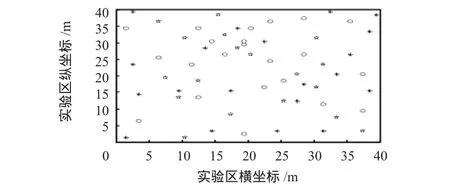
图3 节点部署图Fig 3 Diagram of node deployment

与NSGA-Ⅱ算法对比，MOBPSO算法中粒子群规模PS=20，迭代次数tmax=200，强支配系数C=80。NSGA—Ⅱ算法染色体编码同本文算法编码，交叉率为0.8，变异率为1/Q。

从图4、图5可以看出:随着迭代次数的增加，MOBPSO算法的非劣解集对应的各目标函数（－F1，F2）的均值相对于NSGA—Ⅱ算法更快速、稳定地收敛于较优解。

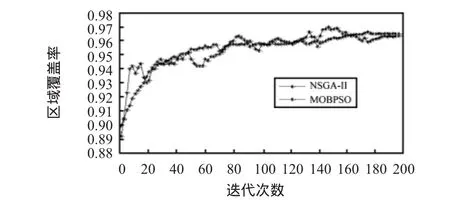
图4 不同迭代次数非劣解对应－F1均值变化图Fig 4 Diagram of－F1value of solution in different iterations

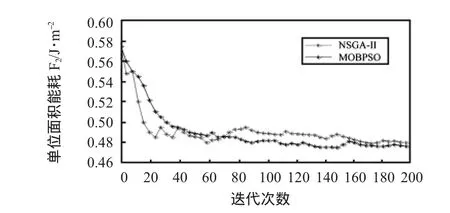
图5 不同迭代次数非劣解对应F2均值变化图Fig 5 Diagram of F2value of solution in different iterations

4 结束语

本文提出了存在“热点区域”的异构无线传感器网络中一种基于二进制粒子群算法的多目标优化的节点部署策略，采用概率感知模型，引入强支配系数使得解分布均匀，结合Pareto最优解选择排序和基于自适应权重的适应度分配，进而获得异构节点部署解。与NSGA—Ⅱ算法相比，运用MOBPSO算法对节点部署后提高了网络覆盖率，同时降低了能耗。本文研究的是二维空间的确定性静止异构节点部署方法，传感器节点位置是通过计算后部署。而监测区域的三维覆盖、节点随机布撒后通过节点移动的部署优化等问题有待于进一步的研究和探索。

［1］Huang Chifu.The coverage problem in wireless sensor networks［C］//ACM International Workshop on Wireless Sensor Networks and Applications，New York，USA，ACM，2005:519 －528.

［2］贾 杰，陈 剑，常桂然.无线传感器网络中最优覆盖节点集的求解算法［J］.东北大学学报:自然科学版，2007，28（11）:1560－1563.

［3］郭怡婷，王俊年.无线传感器网络中基于微粒群算法的优化覆盖机制［J］.计算机与现代化，2009，6:1560 －1563.

［4］黄 亮.基于改进蚁群算法的无线传感器网络节点部署［J］.计算机测量与控制，2010，18（9）:2210 －2212.

［5］林祝亮，冯远进.基于粒子群算法的无线传感器网络覆盖优化策略［J］.计算机仿真，2009，26（4）:190 －193.

［6］Zou Y，Chakrabarty K.Sensor deployment and target of localization based on virtual forces［C］//2003 Proceedings of the IEEE IN FOCOM San Francisco，California:IEEE，2003:1293 －1303.

［7］Shang Y，Shi H.Coverage and energy trade off in density control on sensor networks［C］//Proceedings of 11th International Conference on Parallel and Distributed Systems，Fukuoka，Japan，2005:564－570.

［8］Ciuprina G，Ioan D，Mumteanu I.Use of intelligent-particle swarm optimization in electromagnetic［J］.IEEE Trans on Magnetics，2002，38（2）:1037 －1040.

［9］Laumanns M，Thiele L，Deb K，et al.Combining convergence and diversity in evolutionary multi-objective optimization［J］.Evolutionary Computation，2002，10（3）:263 －282.

［10］阎啸天，武 清.基于GA的网络最短路径多目标优化算法研究［J］.控制与决策，2009，27（7）:1104 －1107.