延迟锁相环的Verilog-A精确建模与仿真*

许望洋，魏廷存，高 武，段延亮

(西北工业大学计算机学院，西安710072)

1 引言

延迟锁相环(Delay Locked Loop，简称为DLL)是一种采用延迟链产生多相延迟时钟、并通过反馈环路控制延迟链精确锁定的一种锁相环结构。它是应用于无线和有线通信、多相时钟产生以及高精度时间-数字转换器(time-to-digital converter，简称为TDC)的重要功能模块。由于DLL是基于时钟的超大规模混合信号电路，在设计时存在仿真时间长、仿真数据量大的问题。尤其是对含DLL的全芯片仿真时，DLL仿真占用大量的空间和时间资源。因此，对DLL进行行为级建模，加快DLL模块的仿真速度，是开发含DLL模块的全芯片电路的重要手段。

目前已提出多种DLL的建模方法，文献［1］建立了离散时间的DLL模型，分析了输入噪声、延迟链噪声和控制电压噪声对DLL抖动的影响。但由于该模型未考虑器件失配和环路电容漏电流的影响，所以对延迟锁相环的建模精度较差。文献［2］对DLL中鉴相器、电荷泵和延迟链模块进行了晶体管级的抖动分析，并建立了基于噪声的DLL抖动模型，但并没有提供精确的Verilog-A模型，因而不能实现行为级仿真。

笔者通过分析模拟DLL抖动来源，建立了各模块的精确Verilog-A模型，从而提高了仿真精度，并缩短了DLL仿真时间，提高了基于DLL的芯片设计效率。第二部分介绍了电荷泵DLL的结构。第三部分在时域分析了噪声和器件失配对抖动的影响，第四和第五部分对DLL进行了建模仿真和分析。

2 电荷泵DLL的结构

传统的模拟延迟锁相环主要由五部分构成［3］:电压控制延迟链(VCDL)、鉴相器、电荷泵、环路滤波器以及启动控制单元，如图1所示。输入时钟Clk_ref经VCDL延迟后，最后一个输出时钟为Clk_out。Clk_ref和Clk_out的相位差被鉴相器检测。为简单起见，这里假设鉴相器检测这两个时钟的上升沿之间的相位差，并且延迟链中延时单元的延时随着控制电压增大而减小。如果Clk_ref的上升沿在Clk_out之前，则Up为高电平，Down为低电平，此时电荷泵中上面的开关导通，下面的开关关闭，这样，电荷泵就给环路滤波电容充电，导致控制电压增大，电压控制的延迟链中的延时就减少，从而使Clk_out的上升沿更接近于Clk_ref，即Clk_ref和Clk_out的相位差减小。由于时钟信号的延时是连续变化的，经过若干个周期的调节后，理论上Clk_ref和Clk_out的相位差变为零，Clk_ref和Clk_out的相位被最终锁定。但由于电路启动时初始状态的不确定性，DLL很容易产生不锁定或者误锁定的现象。为此，在图1中增加了一个启动控制电路，在电路启动时将环路滤波电容预充电至高电平，通过合理的设计，可以使VCDL的初始延迟时间小于一个时钟周期。这样即可消除DLL不锁定或误锁定的现象，当电路进入正常工作后，通过反馈调节可以使DLL的终端输出延时准确地锁定至一个时钟周期。

图1 模拟延迟锁相环的结构

3 噪声及器件失配对DLL抖动的影响

3.1 噪声对DLL抖动的影响

在实际电路中，噪声会使得DLL偏离理想的工作状态，而这种非理想的工作状态会使DLL的多相输出时钟产生抖动，从而影响DLL的延时精度。图2表示DLL中各个模块的噪声对多相输出时钟产生的影响。由图2可知，总的输出抖动可以由各模块的抖动分量通过下组公式计算得到［4］:

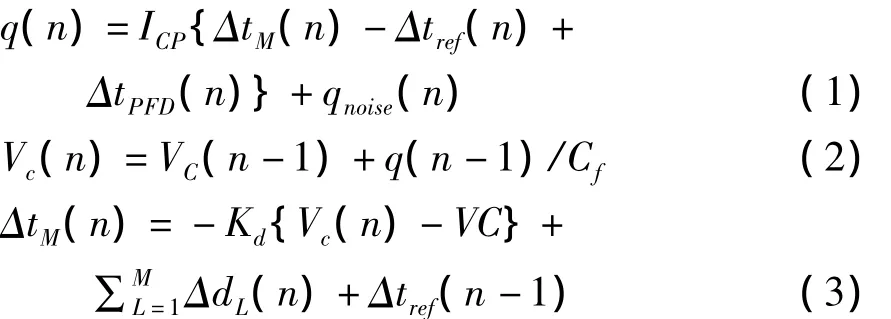
式中q(n)表示电荷泵在第n个时钟周期泵入环路滤波电容的电荷量，ICP表示电荷泵的充放电电流，ΔtM(n)表示第n个时钟周期延迟链输出的时钟抖动，Δtref(n)表示参考时钟的抖动，ΔtPFD(n)表示鉴相器的鉴相误差，qnoise(n)表示环路滤波电容噪声，Cf表示环路滤波电容，Kd表示压控延迟链的增益，ΔdL(n)表示第L个延迟单元在第n个时钟周期时的抖动，VC表示理想状态下DLL锁定时VCDL的控制电压。从上式可以看出，由于噪声所引起的抖动在延迟链中发生了累积，这将导致最后一相输出时钟的抖动值最大。

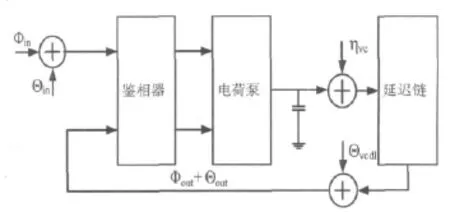
图2 DLL噪声抖动模型

公式(1)-(3)考虑了整个DLL中各个组成模块的噪声对最终输出时钟抖动的影响。为了对DLL进行整体建模，需要先对DLL中各模块进行单独建模，因此需要单独分析各模块的噪声对抖动的贡献。为此，在分析某一个模块的噪声对抖动的贡献时可以暂时将其他模块假设为理想模块，这样可以得到各模块所产生的抖动均方值为:

3.2 器件失配对DLL抖动的影响

由于电路噪声具有随机性，因此对多相时钟抖动的影响也具有随机性，通常认为它符合正态分布。器件失配是在芯片生产过程中由于工艺误差造成的，通常也服从正态分布。但器件失配和电路噪声的区别在于器件失配是由于工艺误差造成的，一旦芯片加工完成，失配的大小也就确定了，所以器件失配最终产生的是固定抖动，而噪声的随机性一直伴随着芯片的整个工作过程，因此噪声所造成的抖动为随机抖动。

器件失配对DLL抖动性能的影响主要表现在延迟单元的失配和电荷泵充放电电流的失配。由于在设计电荷泵时可以将电流失配控制在一个很小的范围内，故在建模时暂时只考虑由延迟单元失配所引起的抖动。

可以对延迟单元的性能进行如下数学描述［5］:

式中dL表示第L个延迟单元的延迟时间，dtune表示延迟单元在控制电压VC下的理想延迟时间，eL(Vc)表示与MOS管的失配等效的控制电压的变化。由此知道，在各延迟单元完全独立的情况下，eL(Vc)的均值为0。同样，在不考虑其他噪声影响的情况下，整个延迟链应该准确的锁定为一个时钟周期。由此，单个延迟单元的延迟时间可以表示为:

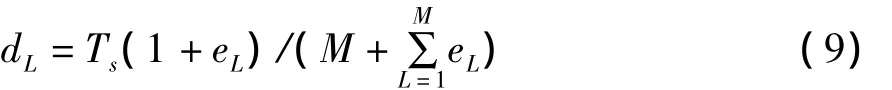
式中Ts表示参考时钟的周期，M表示延迟链的延迟单元数。这样，可以计算出经过m个延迟单元后由于失配所导致的抖动为:

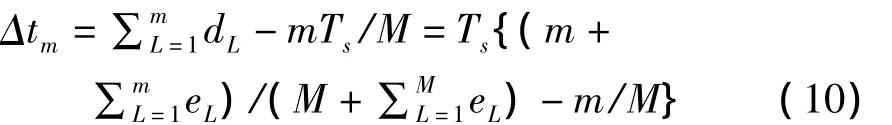
通过上式可得第m个延迟单元后由失配造成的抖动值为:

通过对式(11)的分析可知，当m=M/2时，由失配引起的抖动值达到最大。如图3所示。其中σeL可以通过蒙特卡洛分析得到，通过对150组数据进行正态拟合，如图4所示，可以得到它的σ值为15ps。

从图3中可以看出，当总延迟单元数为32时，第16个延迟单元后的抖动值达到最大(不考虑电路噪声和鉴相器的鉴相误差)，约为44ps。

图3 失配引起的抖动随延迟单元数的变化情况(理想状态下)

图4 延迟单元延迟时间的蒙特卡罗分析

4 DLL各模块行为级模型

4.1 电压控制延迟链的Verilog-A模型

设计的DLL的电压控制延迟链由32个延迟单元构成。这样当输入时钟频率为50MHz时，可以实现625ps的时间分辨率。但是延迟单元的延迟时间随控制电压并不是线性变化，其变化曲线如图5所示。

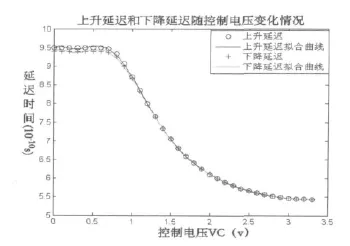
图5 延迟时间随控制电压变化曲线

从图5可以看出，当控制电压由0V变化到3.3V时，延迟时间由950ps变化到550ps。为了提高建模的精确度，需要对该曲线进行多项式拟合。对于延迟单元的相位噪声可以通过PSS+PNOISE仿真得到，其相位噪声谱如图6所示。因此根据文献［6］提出的方法，可以计算出每一个延迟单元由噪声所产生的抖动值约为2.3ps。

图6 延迟单元相位噪声

这样可以对整个电压控制延迟链进行Verilog-A建模如下:

4.2 鉴相器和电荷泵的Verilog-A模型

在DLL中，鉴相器主要用来鉴别压控延迟链的输入时钟与终端输出时钟之间的相位差，然后通过电荷泵将相位差转换为相应的充放电电流。由于电路噪声可能导致鉴相器的鉴相误差和电荷泵充放电电流的失配，使得环路滤波电容上的控制电压产生纹波，最终导致延迟单元的延时抖动。为了便于鉴相器和电荷泵建模，可以将噪声转换为一个等效到鉴相器输入端的相位抖动。通过PSS+PNOISE仿真得到这个等效抖动约为2ps。在建模时，考虑到电路启动时启动控制电路会自动给环路滤波电容充电到高电平，因此在Verilog-A代码中也必须体现这一点。这样，可以对鉴相器和电荷泵统一建模如下:

4.3 环路滤波电容的Verilog-A模型

嵌入到延迟锁相环中的环路滤波电容主要有两个作用，一是生成控制电压，二是作为滤波器来降低噪声。在建模时，控制电压可以通过对流入环路滤波电容的电流进行积分得到。降低噪声主要是靠较大的环路滤波电容对噪声进行滤波来实现。在设计DLL时，采用的环路滤波电容大约为30pf。由此可以对环路滤波电容建模如下:

5 仿真结果及讨论

第四部分对DLL各模块进行了单独建模，现在需要对整个DLL进行整体仿真，以验证建模的正确性。仿真的原理图如图7所示，图中延迟链模块用来产生多相时钟，当电路锁定时，VCDL每相邻两相时钟在理论上相差625ps。

图7(a)为对电路管子级的仿真结果，图7(b)为对Verilog-A建模的仿真结果。两图中从上至下依次是第1、15、31个延迟单元的延迟时间的INL仿真结果。从图7(a)中可以看出，随着延迟单元的增多，其延迟时间的peak-to-peak抖动值也增大，依次约为 8ps，50ps，85ps。这是因为延迟单元的peak-to-peak抖动主要是由电路噪声所造成的。在第三部分中，已经分析了噪声对电路抖动的影响，随着延迟单元的增多，噪声引起的抖动会产生累积，因此最后一个延迟单元的peak-to-peak抖动值会达到最大。同时，可以看到，在图7(b)中三条曲线的均值均不为0，其中中间那条曲线的偏离最大，达到了50ps。这主要是由延迟单元失配造成的。通过第三部分的分析知道，在延迟链的中间由失配造成的抖动值达到最大，这与以上建模仿真得到的结果相符合。

根据模拟延迟锁相环的原理可以知道，延迟链的抖动会导致电荷泵随机地向环路滤波电容充放电，最终表现为环路滤波电容上控制电压的纹波。图8(a)和(b)分别为由电路仿真和建模仿真得到的控制电压的变化曲线，其中下部曲线为DLL锁定后控制电压的局部放大。

图8 仿真变化曲线图

由图8(a)和(b)可知，DLL大约在启动18us后达到锁定状态，锁定后控制电压纹波的peak-topeak值大约为4mV。通过比较图8(a)和(b)可以看到，锁定后建模仿真控制电压稳定在1.909V，电路仿真控制电压稳定在1.875V，误差值约为0.035V，误差小于1.8%，DLL的建模仿真和电路仿真结果能够较好的吻合，因此Verilog-A建模具有较高的精度。

另外，对DLL进行了30us时长的仿真，行为级建模仿真大约耗时3分钟，而电路级仿真需要约3.5个小时。因此，通过建模可极大的缩短仿真时间，提高仿真效率。

6 结束语

在分析模拟DLL抖动来源的基础上，对DLL进行了Verilog-A精确建模与仿真，在保证仿真精度的前提下大大缩短了仿真时间。通过与电路管子级的仿真结果比较可知，建模的精度达到了混合信号仿真的要求。但是由于影响DLL抖动的因素很多，并未能够对所有的抖动源进行建模，需要今后进一步完善。

［1］ Aguiar RL，Santos DM.Modelling charge-pump delay locked loops［C］.Proceedings of ICECS ＇99.The 6th IEEE International Conference on Electronics，Circuits and Systems.，2:823_826，1999.

［2］ Barajas Enrique，Mateo Diego，Jos＇e Luis Gonz ＇alez.Behavioural modelling of DLLs for fast simulation and optimisation of jitter and power consumption［C］.13thEuromicro Conference on Digital System Design:Architectures，Methods and Tools.2010.

［3］ 高武.正电子发射断层成像前端读出芯片设计技术研究［D］.西安:西北工业大学博士论文.2011.

［4］ Beek RCH van de，Klumperink EAM，Vaucher CS.Analysis of Random Jitter in a Clock Multiplying DLL Architecture［C］.ProRISC 2001，12thAnnual Workshop on Circuits，Systems and Signal Processing，Veldhoven，the Netherlands，29-30 November 2001.

［5］ Beek RCH van de，Klumperink EAM，Vaucher CS，et al.Jitter in DLL-Based Clock Multipliers caused by Delay Cell Mismatch［C］.ProRISC 2002，13thWorkshop on Circuits，Systems and Signal Processing，Veloven，the Netherlands，28-29 November，2002.

［6］ Fordahl.Application Note AN-02-3［R］.http://www.doc88.com/p-38231809540.html.