原位检测系统中触发式测头的误差分析与补偿

王立成 黄信达 丁 汉

华中科技大学数字制造装备与技术国家重点实验室，武汉，430074

0 引言

原位检测系统通常是指基于数控机床本体的多轴坐标测量系统，它在不重复装夹情况下可对被加工零件进行在机测量。采用原位检测技术可以及时发现加工误差，并据此修正加工工艺参数，对零件进行补加工；同时可避免零件加工和测量在不同设备上进行而产生的重复定位误差和工时耗费，因此受到了研究者的重视，并得到越来越多的应用［1－4］。该系统在大型工件、复杂曲面或多表面工件制造中的应用需求更为迫切。

由于原位检测时的环境较为恶劣，且影响测量精度的因素众多，所以原位检测系统的测量精度控制比坐标测量机的测量精度控制更困难。目前，原位检测系统一般采用触发式测头，针对触发式测头精度的研究主要集中在坐标测量机检测环境下的测头预行程误差分析［5－8］和测头半径补偿［9－11］两个方面，但考虑到原位检测所处环境的复杂性，对其中测头精度的分析和误差补偿技术的研究有待进一步深入。本文通过分析和实验，对原位检测系统中的触发式测头进行了校准，并提出了一种基于在线标定技术的测头半径补偿方法。

1 原位检测系统的构成与工作流程

本文涉及的零件原位检测实验平台由MIRKON五轴加工中心、Reinshaw OMP40测头系统及DelCam/PowerInspect自动原位检测软件构成。利用该平台，可以对已加工零件进行原位测量，获取被测对象的几何信息，在此基础上，自主开发用于测量误差补偿、形状误差评估和加工误差修正等工艺过程的算法，来解决复杂零件制造过程中出现的问题，实现复杂零件的加工－测量一体化。系统的工作流程如图1所示。

2 测量误差分析与测头校准

原位检测的误差来源为硬件误差、测量规划误差、软件算法误差和环境引起的误差等几个方面。其中，硬件中的测头的误差对测量结果准确性影响不容忽视，在测量前，需要对测头精度进行校准。

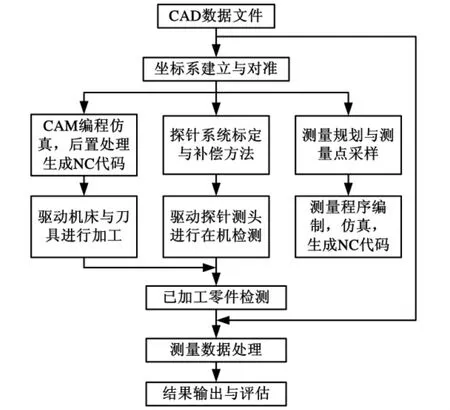
图1 基于原位检测的加工测量一体化方法流程图

2.1 测头误差

测头误差主要为测头安装偏心误差、测头预行程误差和测头半径补偿方法误差。

测头安装偏心误差指测头中心轴线和机床主轴中心轴线的偏差。该误差通常通过千分表进行手工调整，也可先利用原位检测技术计算出测头偏心量，再通过软件进行补偿。

触发式测头本身存在各向异性，导致不同探测距离、触测速度、测杆长度以及测头直径对测头的触发时机产生影响，因而存在一个有规律变化的系统误差——测头预行程误差。可以采用多次触发的方式，减小触测速度变化过大带来的影响，也可以通过标定实验的方法对预行程误差进行检测和补偿。

接触式测量获取的数据是测头中心点的坐标，其与被测对象表面接触点之间相差一个测头半径的距离，为了得到待测对象几何尺寸的真实数据，需要进行半径补偿。但受到测头制造精度和被测对象表面特性的影响，半径补偿值不可避免地存在着误差，故本文提出了一种改进的逐点半径补偿方法。

2.2 坐标系定位

原位检测的一个特点是待测零件的加工坐标系、测量坐标系和模型坐标在系理论上完全重合，省去了测量数据之间的坐标变换，方便进行误差计算。但在使用标定球校准之前，需要调整机床坐标系原点，使其位于标定球的理想球心，保证测量规划的位置和实际测量的位置一致。对准的流程如图2所示，表1给出了机床坐标系原点对标定球球心的对准结果。

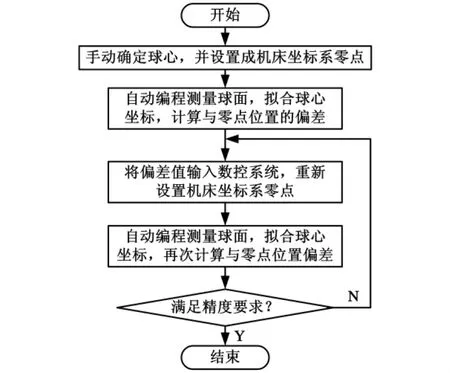
图2 坐标系定位流程图

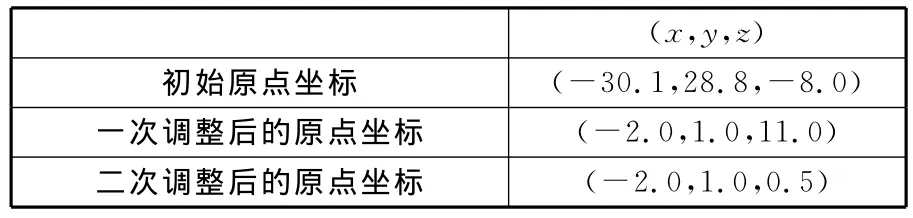
表1 机床坐标系原点对标定球心自动对准实验数据μm

2.3 测头半径校准

因为测头存在预行程误差，所以测头探针头标称直径不能作为测量时的实际作用直径使用，需要进行测头校准。具体的步骤如下：

（1）采用ISO推荐的25点测球法［12］对标称半径为Rcal的标定球进行自动测量，测量结果记录在表2中，测量得到的原始数据是对应测点位置上测头探针头球心的坐标。

（2）对这25点用非线性最小二乘拟合算法拟合球面［13］，得到拟合球面的球心坐标为（－2.8，1.7，1.1）μm，拟合球面的半径Rfit＝10.9286mm。

（3）得到的拟合半径是标定球半径和探针头实际作用半径的和，在假设标定球精度比测头探测精度高很多的前提下，可以得到测头实际作用的半径：

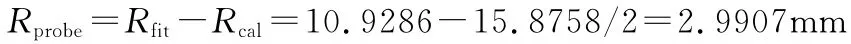
经过上述步骤完成测头半径校准后，将校准过的测头半径输入到数控系统，作为实际测量中的测头半径补偿值进行半径补偿。

以上的校准过程简单实用，是触发式坐标测量系统进行测头校准和半径补偿的必备过程。但依据这种校准方法进行半径补偿，尚未考虑测头在实际测量点处由于触发方向、触发条件不同所导致的补偿半径的误差，而这种误差在原位测量中的效应会更趋明显，成为测量不确定度的一个重要来源。因此，需要有一种面向测量任务的原位标定技术来进一步完善测头半径的补偿方法。

3 测头误差补偿

3.1 考虑测头偏心的误差修正

由于探针或测头安装导致的测头偏心误差会使实际测量位置偏离基于CAD模型规划的测量点，从而发生测量点与名义值之间的误对准。修正测头偏心误差就是根据实际测量点坐标寻找与之对应的名义点坐标，重新计算二者之间的误差。测头偏心修正方法如图3所示。

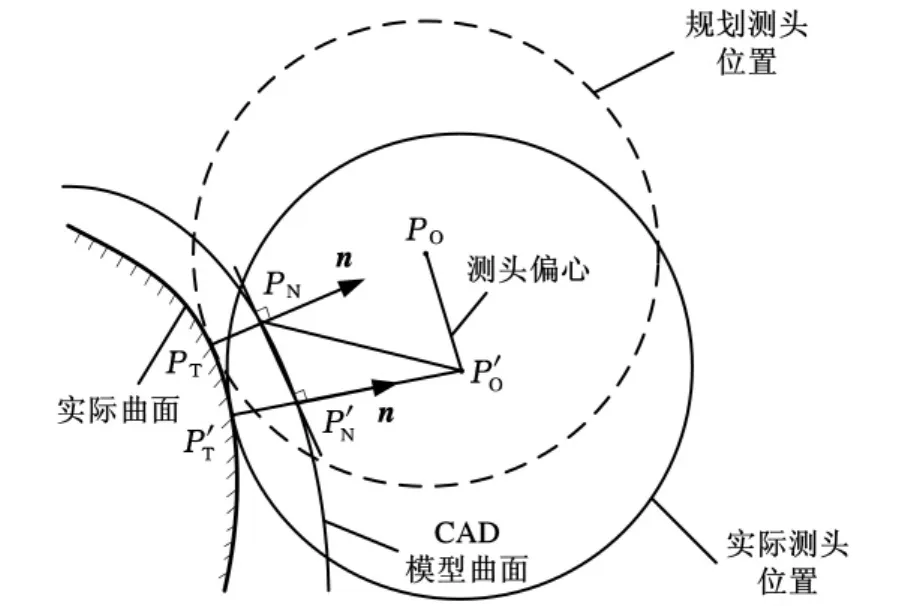
图3 测头偏心修正示意图

图3中，PN是不考虑偏心时CAD模型上的规划测点，P′O是存在偏心时得到的测头实际中心点，P′T是完成半径补偿后的被测表面接触点，当存在测头偏心时，实际测点P′T所对应的CAD模型上的名义点为P′N点，通过计算｜P′TP′N｜，才能获得准确的测量结果。

通常情况下，偏心量和测头探针头半径相比很小，所以假设被测曲面名义点变化所引起的曲面曲率变化可以忽略，即规划的测点PN处法矢n和实测后名义点P′N处的法矢相同，那么可以利用已知的PN、P′O和n，通过内积公式求出P′O和P′N两点之间的距离：

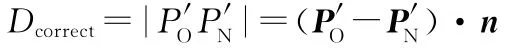
又因为测头探针头补偿半径Rprobe已知，所以计算出实际测点P′T与修正后的名义点P′N之间的误差e（e＝Rprobe－Dcorrect）后，可完成测头偏心误差的单点修正。

3.2 基于在线标定技术的半径补偿

在基于标定球的测头校准基础上，对触发式测头原位检测的半径补偿方法改进。改进方法的基本思想是：将被测零件和标准球同时放置在工作台上，零件测量前，利用标定技术建立测头半径补偿的误差列表，并使用双线性插值算法得到曲面任意位置的法矢信息及其对应的测头半径补偿值，再根据实际测量点的法矢信息，建立实际测量位置和误差列表之间的映射关系，通过搜索误差补偿列表，找到对应的测头半径补偿值，实现逐点半径补偿。详细的算法流程如图4所示。

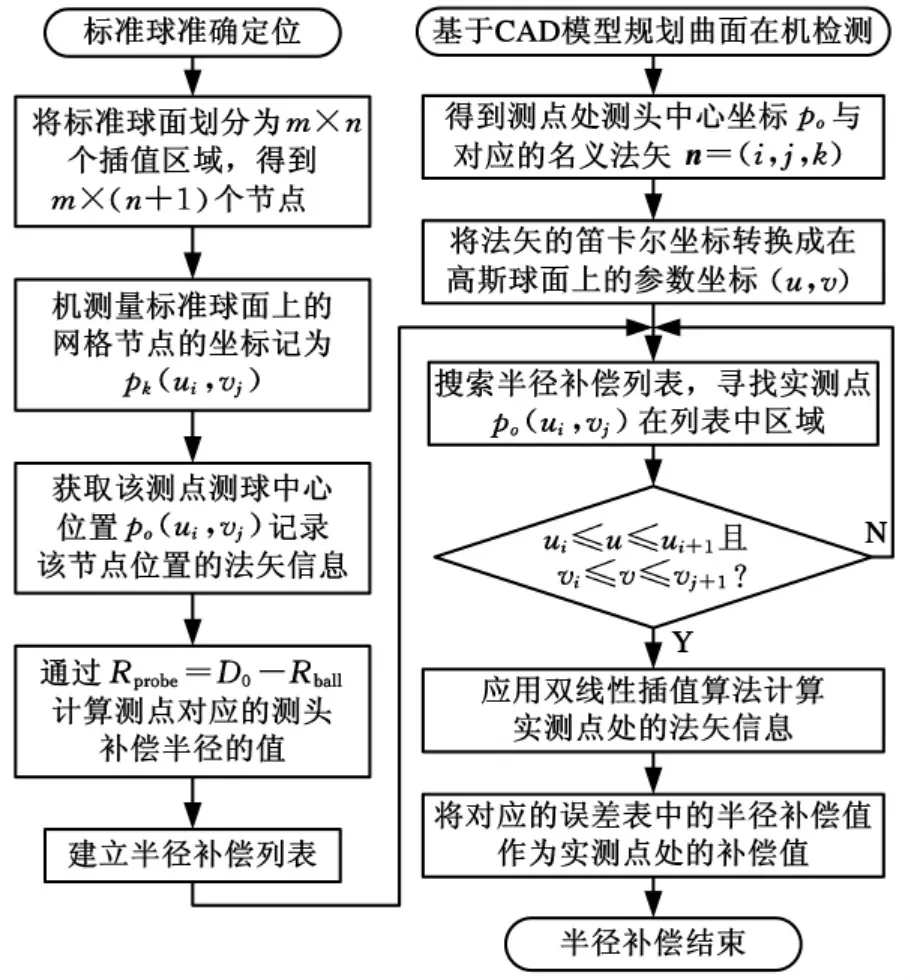
图4 半径补偿流程图

3.3 实验验证

为了评价本文中提到的补偿算法，实验中将一个标定球面作为标准曲面进行了验证实验（图5）。首先在标定球的上半球面上采集181个点，并以采集点作为节点在半个球面上划分网格，根据每个节点处的测头探针头的实际作用半径建立半径补偿列表（表3）。然后通过双线性差值算法得到半个球面上不同法矢处的半径补偿值，图6给出了半个球面不同法矢方向上的测头半径补偿值的变化。

图5 原位检测在线标定与测量实验

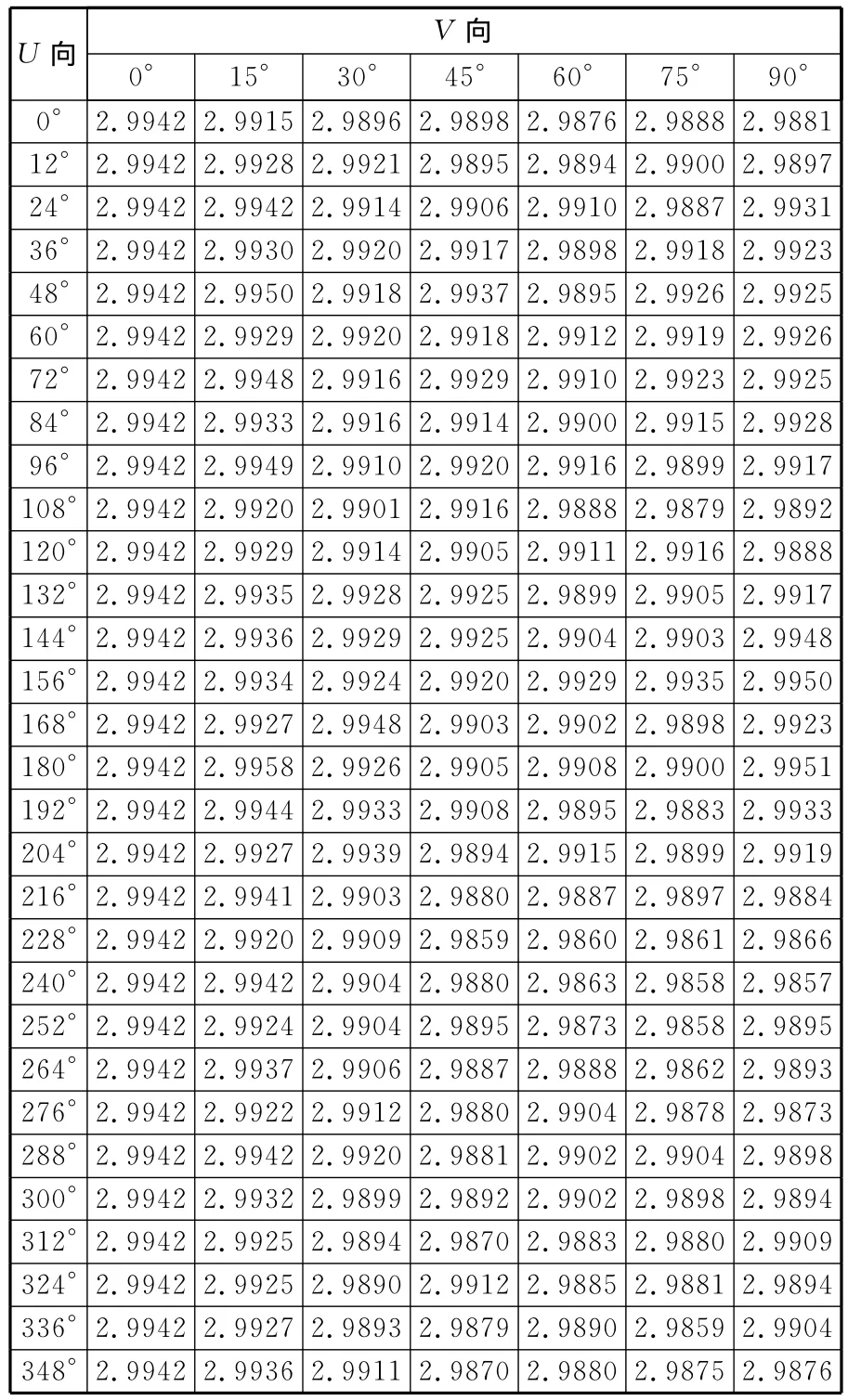
表3 基于标准球面的网格节点半径补偿误差列表mm

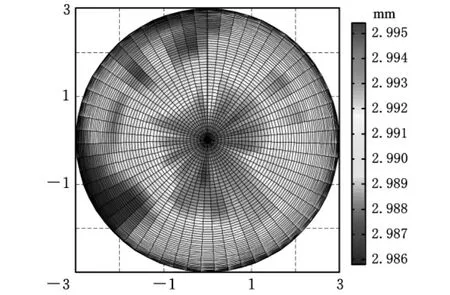
图6 测头半径补偿误差分布示意图

在同一个环境下再测量一个直径经过标定的球面。将本文的补偿方法和商用测量软件所带的补偿方法进行对比，结果见图7和表4。从表4数据可见，所提出插值补偿方法得到的测量结果中，极差、均值误差和标准差都比商用软件所使用的定值补偿方法要小，从而验证了本文提出方法的有效性。

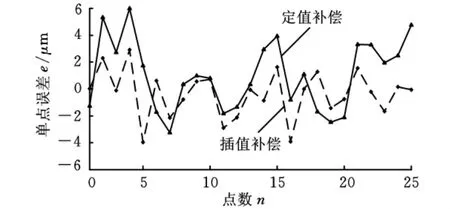
图7 不同半径补偿方法单点误差比较结果

表4 不同半径补偿方法的统计结果比较 μm

3.4 适用性分析

本文提出的半径补偿是面向现场标定和具体测量任务的误差补偿方法，假设被测表面的法矢信息没有显著的变化，测头探针可以比较准确地获得规划时被测点处的法矢。这在测量大型平坦曲面时，或者在所使用的原位检测测头存在较大的系统误差的情况下，该方法具有更明显的优势。另外，与传统的测头探针半径补偿取一个固定的值相比，该方法更准确反应了实际测量对象的特点和实际测量的过程，可以减小测量的不确定度。

4 结论

（1）给出了原位检测工作流程，实现了复杂零件的原位检测。

（2）分析了原位检测系统中触发式测头的误差来源，对测头偏心和预行程导致的误差进行了校准。

（3）提出了基于在线标定技术的测头半径补偿方法，实验验证该方法比商用软件中采用的半径补偿方法精度更高。

［1］Mears L，Roth J T，Djurdjanovic D，et al.Quality and Inspection of Machining Operations：CMM Integration to the Machine Tool［J］.Journal of Manufacturing Science and Engineering，2009，131（5）：051006.

［2］Cho M W，Kim G H，Seo T.Integrated Machining Error Compensation Method Using OMM Data and Modified PNN Algorithm［J］.International Journal of Machine Tools and Manufacture，2006，46（12/13）：1417－1427.

［3］Zeleny J，Janda M.Automatic On－machine Measurement of Complex Parts［J］.Modern Machinery Science Journal，2009，3：92－95.

［4］李斌，孙忠林，彭芳瑜，等.叶片零件在线检测测点规划问题研究［J］.中国机械工程，2008，19（5）：540－542.

［5］Weckenmann A，Estler T，Peggs G，et al.Probing Systems in Dimensional Metrology［J］.CIRP Annals－Manufacturing Technology，2004，53（2）：657－684.

［6］Estler W T，Phillips S D，Borchardt B，et al.Error Compensation for CMM Touch Trigger Probes［J］.Precision Engineering，1996，19（2/3）：85－97.

［7］Wozniak A，Dobosz M.Influence of Measured Objects Parameters on CMM Touch Trigger Probe Accuracy of Probing［J］.Precision Engineering，2005，29（3）：290－297.

［8］刘丽冰，刘又午，赵小松，等.加工中心在线检测误差补偿技术研究［J］.中国机械工程，2000，11（3）：313－316.

［9］Xiong Zhenhua，Li Zexiang.Probe Radius Compensation of Workpiece Localization［J］.Journal of Manufacturing Science and Engineering，2003，125（1）：100－104.

［10］Srinivasan S，Kovvur Y，Anand S.Probe Radius Compensation for On－machine Measurement of Sculptured Surfaces［C］//Proceedings of ASME International Mechanical Engineering Congress and Exposition.Anaheim，CA，USA，2004：913－920.

［11］Erkan T，Mayer R，Wozniak A.Surface Probing Simulator for the Evaluation of CMM Probe Radius Correction Software［J］.International Journal of Advanced Manufacturing Technology，2011，55（1/4）：307－315.

［12］海克斯康测量技术（青岛）有限公司.实用坐标测量技术［M］.北京：化学工业出版社，2007.

［13］Shakarji C M.Least－squares Fitting Algorithms of the NIST Algorithm Testing System［J］.Journal of Research of the National Institute of Standards and Technology，1998，103（6）：633－641.