基于主体变量的住房价格批量评估

刘洪玉，杨振鹏

（清华大学 房地产研究所，北京 100084）

0 引言

2011年新年伊始，房地产税改革成为人们热议的话题。在“十二五”规划建议中，将“加快财税体制改革”放到了重要位置上，并明确提出“研究推进房地产税改革”。重庆、上海决定自2011年1月28日开始对部分个人住房征收房产税，开创了我国住房制度改革以来向个人拥有住房征收财产税的先河，是我国房地产税改革历程中的重要进展。在这样的背景下，房地产计税价值评估问题得到越来越多的关注。不少学者提出，由于房地产税应以财产的评估价值作为计税依据，因此住房价格的评估技术是房地产税具体实施过程中的关键问题之一[1]。

在以往的文献中，计算机辅助批量评估法（CAMA）常被认为是在数据充足情况下行之有效的实用方法[2][3][4]，其中，又以多元回归分析（MRA）最为常用。例如，纪益成、傅传锐（2005）使用EViews软件的线性回归功能，给出了一个对30套住房进行批量评估的范例[5]；乔治敏等（2009）采用SPSS软件多元线性回归模型对北京4个城区400多套住房的批量评估进行实证研究[6]；龚科等（2010）使用MATLAB软件和LS-SVMLAB工具包，以最小二乘支持向量机的方法进行了小规模的实验[7]。

本文采用方法与以往文献的主要区别，在于利用主体变量代替小区层次的特征变量引入多元回归模型。这一方法既可以减少收集住宅小区层次属性信息的工作量，还能在一定程度上改善模型的评估效果，在未来的实践中具有较好的推广价值。

1 理论基础

1.1 住房特征价格理论

住房特征价格理论与房价的多元回归分析（简称MRA）经常有着密切的联系，不过特征价格理论是一种解释房价形成机制的经济学模型，而MRA是一种统计分析方法。住房特征价格理论（或称Hedonic理论）假设住房由一组特征组成，人们对每一个特征都会具有一定的支付意愿，因此每一个特征实际上都有对应的隐含价格，而人们为购买一套房屋支付的总价，就是这些隐含的“特征价格”的总和[9]。

举例来说，假设在某个市场中，住房包括m个关键的特征，用X1、X2、…、Xm表示某套住房包含每个特征的量，C1、C2、…、Cm分别是这些特征的“单价”（即特征价格）。那么住房价格HP应当为：

在式（1）中，μ是一个随机干扰项，它反映了房屋交易价格还会受到其它不确定因素的影响。

由于特征是不能单独交易的，因此特征价格C1～Cm都是隐含的属性。不过房屋交易价格HP和特征X1～Xm的取值是能直接观测到的，因此，当观测到足够多的交易样本后，就可以通过MRA方法反求HP关于X1～Xm的回归表达式。

1.2 基于MRA的住房价格批量评估

图1 MRA法批量评估的流程

1.2.1 流程

将MRA方法用于住房价格批量评估，一般包括以下步骤。

在进行批量评估之前，首先需要收集足够数量的住房可比交易案例，将这些可比案例的价格和房屋信息整理成标准格式的数据库。同时，还需要整理待评估住房的特征信息，按照同样的格式录入数据库。完成数据整理后，即可运用多元回归分析求取房价关于住房特征的回归表达式。最后，依据回归表达式和需要评估住房的特征数据，完成房屋价格评估值的计算。

1.2.2 常用的房屋特征

常用的房屋特征可分为区位属性、邻里属性和物理属性3大类。区位属性是房屋所在区位的性质，如交通可达性（是否靠近地铁、到市区距离等）、周边配套设施齐全程度、自然环境条件等。邻里属性是更细区域的性质，结合我国居住社区的特点，可理解为小区（楼盘）或街道的属性，如物业管理水平、容积率、绿化率、车位数量等。物理属性即房屋自身的特征，如房龄、楼层（建筑的总层数以及房屋所在层）、朝向、建筑面积、卧室数量等等。

1.2.3 回归模型的设定

应用MRA方法，要求因变量和自变量都是实数数值。对于因变量，通常选用的是房屋总价或单价的自然对数。对于反映房屋特征的自变量，其构造方法则有一定技巧。

有一部分房屋特征本身可以被量化（如建筑面积等），这类特征可以直接作为自变量引入模型，或者将它们的Box-Cox变换形式引入模型。

还有一些房屋特征只可能有若干种固定的取值（后文简称字典型变量），如所在行政区、土地等级、产权性质等，这类房屋特征通常要以虚变量组的形式引入回归模型。以“所在行政区”为例，假设所有考察样本来自4个行政区——城东区、城西区、城南区、城北区，那么只需要“是否属于城东区”、“是否属于城西区”和“是否属于城南区”3个虚变量就可以确定一套房屋所在的行政区。每个虚变量都是在条件成立的时候取值为1，不成立的时候取值为0。这样，就可以用实值变量组代替字典型变量。

最后，模型中一般还包括常数项。计量模型如式（2）所示。

其中，HPi是样本i的房价，X1i～Xmi是依据样本 i的房屋特征转化的自变量组。

2 引入主体变量的MRA

2.1 主体变量的定义

主体变量是反映房屋是否属于某个特定小区的虚变量。如果考察范围内有N个小区，依次是小区1、小区2、…小区N，那么可以用N-1个虚变量P1～PN-1确定房屋所属的小区。

在多元回归分析中，将主体变量P1至PN-1引入回归模型，就可以得到每个小区的主体变量系数，即该小区的价格调整系数。

2.2 引入主体变量的原因

传统MRA方法使用小区层面的特征变量（如绿化率、容积率等）反映房屋所在小区的属性。在评估过程中，这种模型需要根据小区属性的取值进行价格调整。引入主体变量的MRA则采用了更为直接的思路，对每个小区单独设置一个调整系数。在评估中，只需要知道房屋属于哪一个小区以及该小区的调整系数，就可以计算评估价格，而不需要知道这个小区的属性。图2显示了这种思路和传统MRA评估的区别。

图2 引入主体变量的MRA评估过程与传统过程的差异

在非MRA的批量评估中，一般会采用更直接的方式处理小区因素对价格的影响。例如在基于“市场比较法”的评估中，会选取同一个小区（或周边档次相近的小区）的房屋交易作为可比案例。耐人寻味的是，在基于MRA的批量评估中，已有文献往往放弃直接设立小区调整系数的方法，而是间接地在模型中引入小区属性[6][7]。本文后续部分将讨论是否可以通过引入主体变量，使MRA评估也能直接地反映小区因素对价格的影响。

2.3 引入主体变量对模型产生的影响和注意事项

在小区数目众多的情况下，向回归模型中加入主体变量，会大幅增加自变量的数目。这对于MRA模型的影响主要体现在以下三个方面。

2.3.1 自变量意外线性相关

当模型中引入了多组虚变量，有可能意外地出现自变量完全线性相关的情况。例如，在引入主体变量的同时还引入了“所在环线位置”的特征，各小区“所在环线位置”如表1所设定。

表1 造成自变量线性相关的示例

在MRA模型中，设定P1～P6共6个主体变量，用于标记房屋所在的小区。用两个虚变量R1、R2代替“所在环线位置”这个字典型特征——R1表示房屋处于二环以内、R2表示房屋处于二环至三环之间。

不难推导出，对于任何房屋样本，下列关系永远成立：

由于R1、R2可以被主体变量线性表出，因此不能将它们加入到回归模型中。更一般地，任何小区层面上的特征变量都不应与主体变量同时出现。

2.3.2 多重共线性

即便消除了完全线性相关的自变量，多重共线性问题仍有可能存在。特别是在使用新房数据时，应注意主体变量和由交易时点转化而来的月份虚变量往往高度相关。这是因为新房的销售期往往较为集中，已知一条样本所属的小区，就能基本确定它的交易时点大致在某几个月份之间。虽然单纯的多重共线性问题不会影响系数估计量和评估结果的无偏性，但是模型给出评估值的置信区间会更大，对于使用者而言，只能更保守地看待评估结果。因此，对新房进行批量评估时，需谨慎使用主体变量。

2.3.3 模型自由度降低

在样本量不足的情况下，引入较多主体变量会降低模型的自由度。因此，在使用主体变量时必须注意样本量是否显著多于自变量的数目。

3 实证检验

3.1 数据

本文通过实地调研采集了403条二手房出售数据。样本分布在北京市4个居住项目较密集的地区，分别是丰台区的青塔地区、光彩路地区，石景山区的鲁谷地区，以及位于丰台、海淀、石景山交界处的玉泉路地区。选择上述地段的原因之一是，作者对这些区域有一定的了解，容易分辨房源信息的真实性。403套房源来自于46个住宅小区，建筑年代从80年代到2010年不等。其中两个小区按经济适用住房管理（交易过户时补交3%土地出让金），其余小区均可作为商品住房交易。

数据主要通过经纪机构门店采集，时间从2011年3月上旬开始至4月初结束。其中价格信息为各经纪机构信息系统中的业主真实报价，标的房屋均经过经纪人实地踏勘并拍照，具有较好的真实性。此外，数据还由经纪人进行一轮筛选，去除根据其经验认定不可能在一个月内售出的高报价样本，以及采取了明显低报价策略的样本。

反映房屋特征的变量包括以下几项。在小区层面上，作者收集了小区建筑年代、所属行政区、环线位置、容积率、绿化率、物业服务费率等数据，以及“是否按经济适用住房管理”、“1公里内是否有地铁站”等2项虚变量。对于房屋的物理属性，数据集包含建筑面积、所在楼层、建筑总层数、朝向、卧室数量等5个变量。

在研究中，将样本分为“建模样本”和“评估样本”两个部分①对每一条样本生成一个0-1之间的随机数，如果数值大于0.25，则设定该样本为“建模样本”，否则为“评估样本”。抽样后确定了302条“建模样本”和101条“评估样本”。。首先，使用“建模样本”进行回归计算，生成批量评估模型；然后利用模型对“评估样本”的价格进行评估，并与实际价格比较，从而对评估效果进行评价。

3.2 传统MRA模型

传统MRA模型引入小区层面的特征变量，模型初始自变量列表如表2所示。

本文利用清华大学开发的批量评估软件CFMA完成回归计算。CFMA内置的算法采用OLS回归，自变量首先全部引入，之后按t-统计量绝对值由小到大排序，逐一进行多余变量检验，删除多余变量。最终保留了24个自变量，回归结果如表3所示。

模型的拟合优度达0.952。随机扰动项的方差为9.55%，由于被解释变量是房价的对数，据此可以推算，评估价格的1倍标准误差区间是(-9.10%,+10.02%)。对参与建模的302个样本而言，平均绝对预测误差（MAPE）为6.71%。上述数据说明，使用该模型进行评估，误差水平在10%左右，具有一定的实用性。

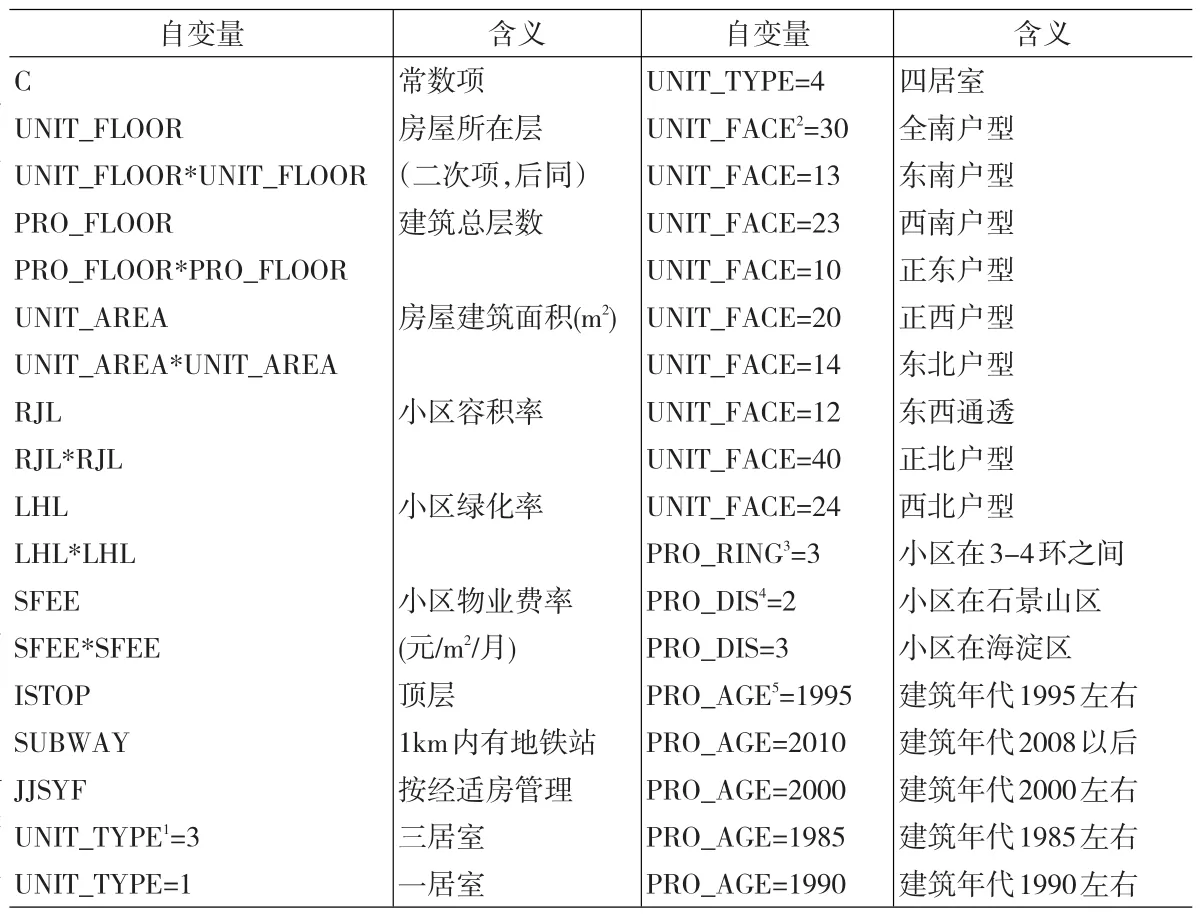
表2 传统MRA批量评估模型初始自变量列表

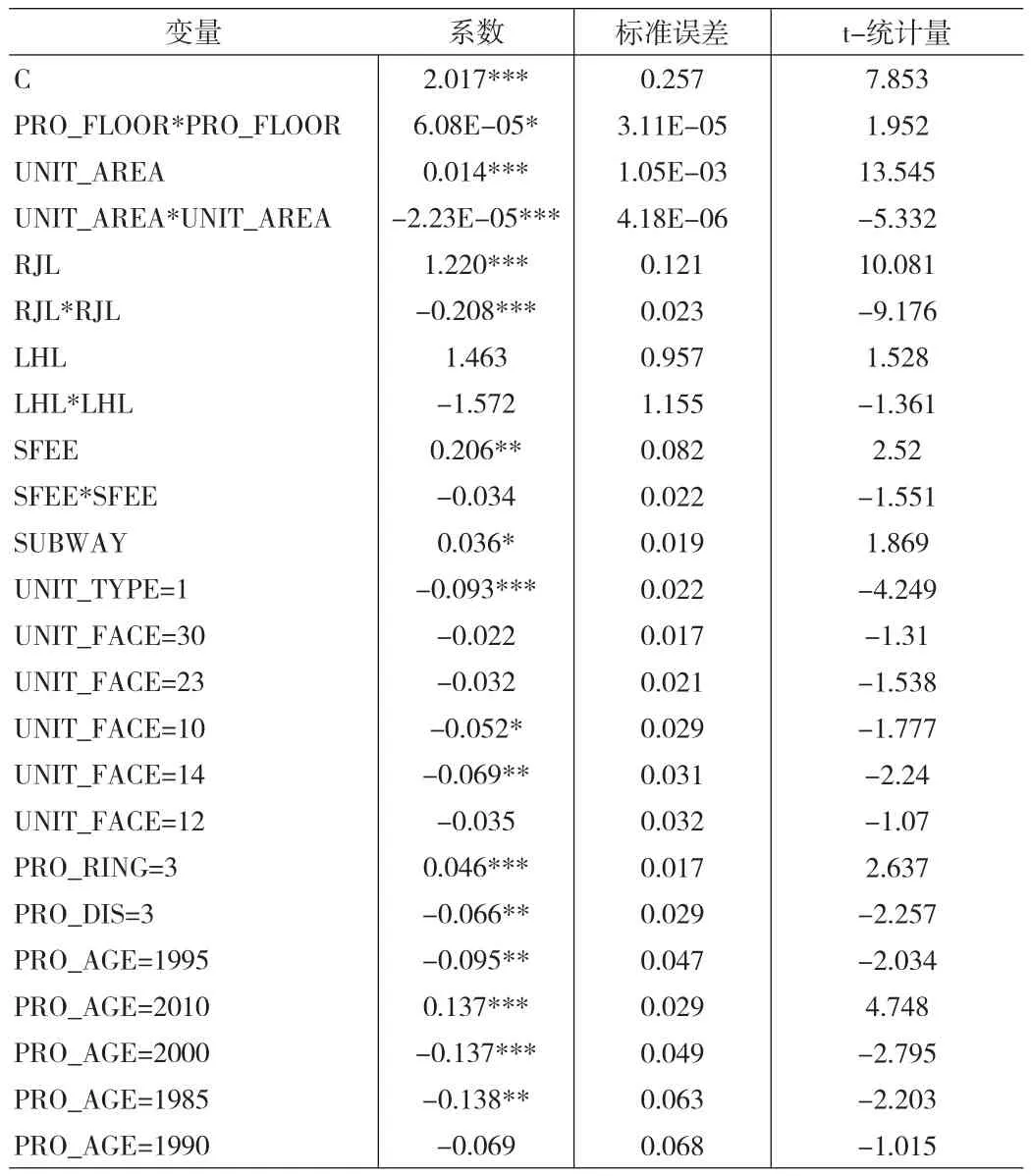
表3 传统MRA批量评估模型回归结果

回归模型自变量的系数还可以揭示影响房价的因素。从表3中可以看到，房屋建筑面积、小区容积率对房价的影响最为显著，且影响程度呈二次变化规律。其他显著水平达到5%的影响因素还有：物业费率与房价正向相关；一居室的价格水平低于其他户型；东北朝向房屋价格低于默认户型（南北通透）；3环～4环之间小区的价格更高；海淀区（只包含玉泉路的两个小区）价格偏低；建筑年代为“2010年”的小区价格最高，“2005年”次之，其他更早年代的小区价格更低。

得到评估模型后，用其余没有参与建模的101个样本检验评估效果。每个样本的实际价格记为Si，评估价格记为Ai，评估价格与实际价格之比记为ARi。采用下述国际评估师协会（IAAO）建议的评价标准衡量评估效果。

表4 传统MRA模型评估效果

平均AR和中位数AR衡量评估的准确程度。IAAO在1999年的《Standard on Ratio Studies》中要求评估比率在0.9～1.1之间。价格相关差PRD衡量按价格加权平均的评估比率，与简单平均的评估比率是否一致。如果PRD低于0.98，说明评估模型将明显高估高价住房、低估低价住房（激进）；如果PRD高于1.03，说明出现相反的情况（保守）。离散系数COD衡量评估误差的分布，它与MAPE类似，区别在于COD衡量相对于AR中位数的偏差。如果AR的中位数恰好是1，COD与MAPE将完全一致。

表5 各小区编号和样本量

从表4可以看到，传统MRA模型的评估效果满足IAAO提出的标准。

3.3 引入主体变量的MRA模型

将样本覆盖的46个居住小区编为1～46号，各小区样本量如表5所示。

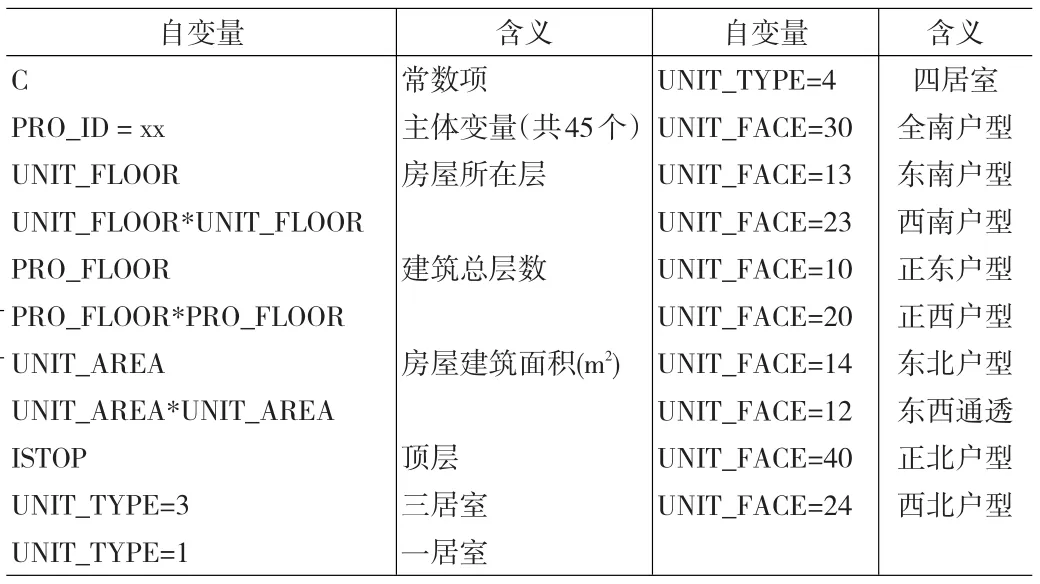
表6 引入主体变量的MRA批量评估模型初始自变量列表

选取样本量最大的小区（彩虹城）作为默认小区，对其余45个小区设置主体变量。由于引入了主体变量，不再引入小区层次的特征，初始自变量列表如表6所示。

同样，使用CFMA批量评估软件完成变量筛选和回归计算，最终保留了46个自变量。回归结果如表7所示。

可以看到，使用主体变量的MRA模型比使用小区属性的模型具有更高的拟合优度。同时，赤池信息量准则（AIC）统计量也得到减小，说明增加的自变量带来了有用的信息。评估价格的1倍标准误差区间缩小为(-8.48%,9.26%)，样本内预测的平均绝对误差（MAPE）降低至5.51%。

应用这一模型，对其余样本进行评估，效果如表8所示。

从表8中可以看到，引入主体变量的模型在评估的准确度和一致性上都有一定提升。但是，评估误差超过±10%的案例数增加了1例。

综合考虑上述实证研究结果，可以发现：引入主体变量的MRA模型在不使用小区层面特征信息的情况下，评估效果能够等同于甚至超过使用小区信息的传统模型。

4 结论和建议

本文设计了一种基于主体变量的房价批量评估模型。该方法与传统多元回归分析（MRA）模型的主要区别在于，使用小区虚变量（主体变量）代替所有小区层面的特征变量。本文进行这一调整背后的原因是，传统MRA模型通过小区的各项属性间接确定该小区的价格调整系数，本文认为直接从回归中获取小区价格调整系数更能有效地利用信息。

使用引入主体变量的MRA模型，不但能够减少收集小区属性信息的工作量，评估效果也并未降低。实证研究显示，引入主体变量的模型在大多数统计量和评价指标上优于传统MRA模型。

表7 引入主体变量的MRA批量评估模型回归结果

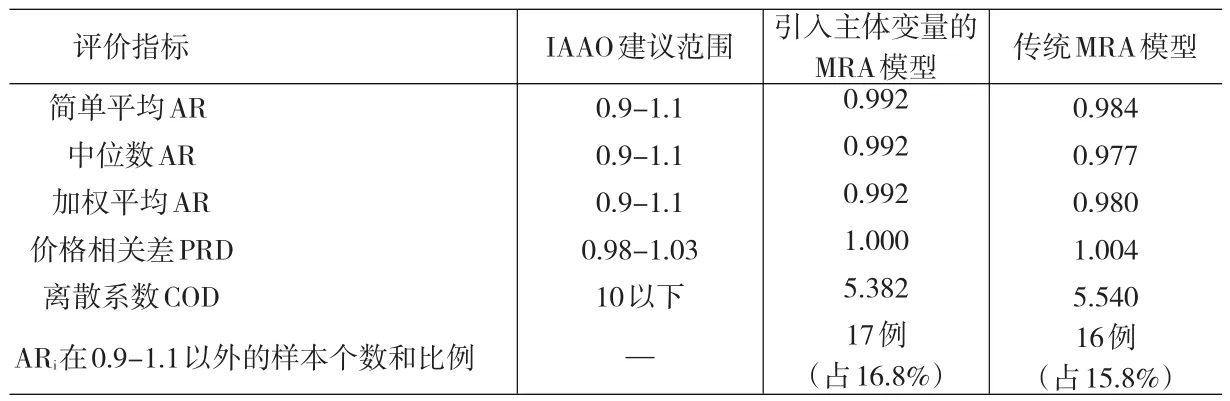
表8 引入主体变量的MRA模型评估效果与传统模型的对比

本文研究成果对于在我国开展住房价格批量评估具有一定现实指导意义。特别是在数据收集方面，提示评估机构应当将工作重心放在采集价格信息和房屋的物理属性上，而不必投入大量的人力、财力整理小区层次的信息，也没有必要过分依赖地理信息系统。通过简单地添加主体变量进入回归模型，就可以获得更好的评估效果。

[1]高云才.积极稳妥推进房地产税改革[N].人民日报,2010-12-06(17版).

[2]任作风,廖俊平.计算机辅助批量评估法（CAMA）在物业税估价中的应用[J].中国房地产估价师,2005，(1).

[3]纪益成,王诚军,傅传锐.国外AVM技术在批量评估中的应用[J].中国资产评估,2006，(3).

[4]刘洪玉.计算机辅助批量评估：国际经验与我国的应用前景[J].中国房地产估价与经纪,2007，(6).

[5]纪益成,傅传锐.批量评估：从价税的税基评估方法[J].中国资产评估,2005，(11).

[6]乔志敏,李德峰,邹文军,周战强.基于财产税征收的不动产价值评估——对北京市4个内城区的实证分析[J].城市发展研究,2009，(3).

[7]龚科,肖智,李丹.基于支持向量机的物业税税基批量评估[J].涉外税务,2010，(5).

[8]John D.Benjamin,Randall S.Guttery,C.F.Sir⁃mans.Mass Appraisal:An Introduction to Multiple Regression Analysis for Real Estate Valuation[J].Journal of Real Estate Practice and Education,2004，(7).

[9]S.Rosen.Hedonic Prices and Implicit Markets:Product Differentiation in Pure Competition[J].The Journal of Political Economy,1974,82(1).