基于非线性GRA的群体模糊多属性决策模型

李香花,边 宁,,,王孟钧

（1.中南大学土木工程学院,长沙410075;2.株洲市城市规划局,湖南 株洲421007）

0 引言

由于客观事物复杂性和不确定性以及决策者主观意见的模糊性，群体模糊多属性决策（GFMADM）问题越来越受理论界与实务界关注。群体模糊多属性决策方法作为一种能够对备选方案的数量属性和质量属性进行高度综合的评价方法，在系统优化、经济评价与方案决策中得到广泛应用。目前，有关GFMADM的理论研究已取得了丰硕的成果[1-9]，综合起有来主要理想点法（TOPSIS）[1-6]和线性规划法（LINMAP）[7-9]两类方法。文献[1]先通过集结专家群体意见得到综合评判矩阵，然后设定属性权重和正负理想点并依据距离关联做出综合评判；文献[2～4]根据属性值差异与属性权重的关系分别采用极值偏差法、模糊向量投影技术、灰色关联法和优势度关联法构建函数，求解属性权重值，然后从规范化综合决策矩阵中选取正负理想方案，并根据备选方案与理想方案的距离、投影或关联度等进行加权集结与决策评价；文献[5]依据属性优势度关系确定属性的权重以及优势度矩阵，并依据优势度概率测度值进行决策；文献[6]侧重对决策者群体意见的一致性进行研究与集结，然后通过到正负理想点的距离进行决策；文献[7～8]则利用线性规划模型求解属性权重值和理想方案属性值，然后依据备选方案与理想方案的差异度进行决策。由于决策属性的权重与属性值的大小没有必然的联系，理想的方案值并不一定存在于决策矩阵中，因此理想点法中理想方案的直接选取难以排除主观因素的干扰。文献[7～9]的线性规划（LINMAP方法）涉及参数过多，计算量大，因此现实应用推广存在一定困难。本文在已有成果基础上，针对决策问题的模糊性和不确定性，建立三角模糊决策矩阵，并综合LINMAP和TOPSIS的优点，运用模糊环境下备选方案到理想方案的距离，分析群体决策偏好的一致度和不一致度，构建群体多属性决策的非线性目标函数，并借助MATLAB、EXCEL等辅助计算工具，求解函数得到理想方案属性值及属性权重值。然后结合决策属性值群体意见的相关性，运用灰色关联法计算各备选方案与理想方案综合加权关联度，据以进行方案的决策排序。最后通过算例检验。为群体多属性决策问题提供新思路。

1 三角模糊数预备知识

定理1若a=(al,am,,au) ,0＜al＜am＜aua͂=(al,am,,au),0＜al＜am＜au,则a͂为一个三角模糊数，其隶属函数可以表示为：

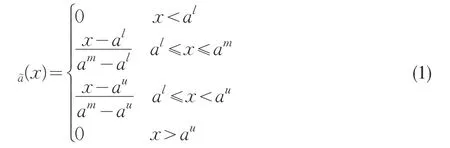
由此，三角模糊数隶属函数必在区[0,1]上。

定理2 有任意两个三角模糊数a͂=(al,am,au)=(bl,bm,bu)，根据拓展原理有如下运算规则：

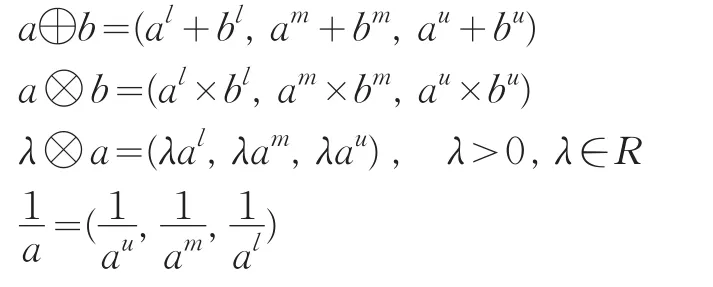
其中⊕ , ⊗为三角模糊数的加法、乘法运算符号；λ为一常数。

效益型属性为:

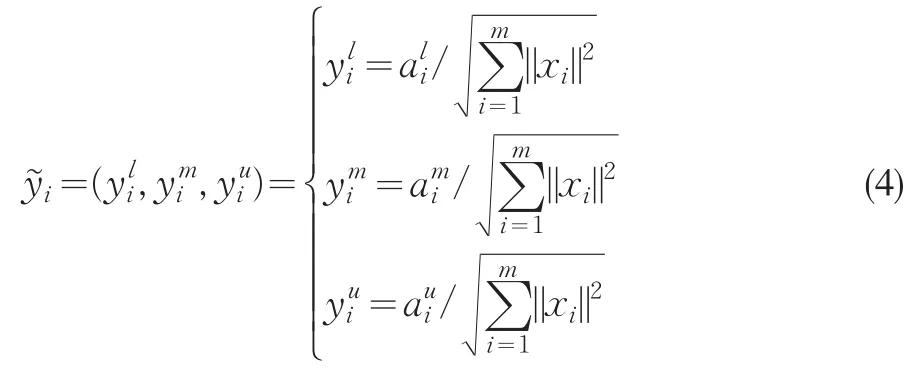
成本型属性为:

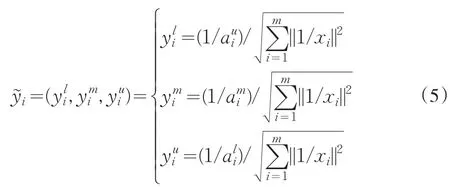
定理6若α,β为两个三角模糊数向量，，其中（i=1,2,…,m），则α与β的关联系数可以表示为ξi：

式中ρ为分辨系数，依据决策的精准度来确定。

2 模糊多维属性非线性GRA模型

若决策中有n个备选方案组成备选方案集合X=(x1,x2,…,xn)，m项决策属性组成属性集合U=(u1,u2, …,um)，则决策问题为多维属性决策，常用的方法有理想点法（TOPSIS）和线性规划法（LINMAP）。这两种方法都存在一定的局限性。本文结合两种方法的基本原理的基础上，采用非线性函数变换，构建多属性非线性决策模型，求解理想方案值和权值，并运用灰色关联法来进行决策，具体过程如下：

Step 1设定语言变量，并根据决策专家对各备选方案的各属性模糊评价，构成多数性模糊决策矩阵其中根据公式(4)与（5）对矩阵的模糊数值进行归一化，得到标准决策矩阵决策属性权重向量为ω=(ω1,ω2, … ,ωj)，其中Step 2设定理想方案为A*的属性值为:

=则各备选方案到理想方案的欧几里德距离为di,i=1,2,…,n。

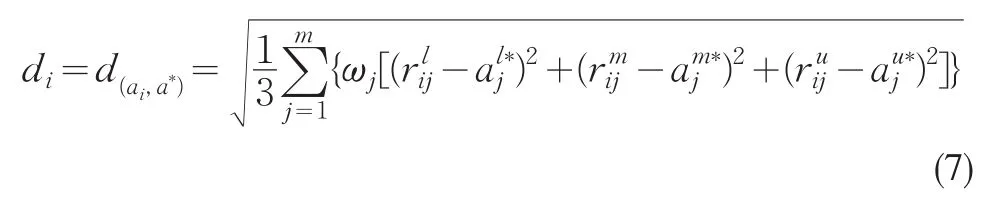
Step 3已知专家决策偏好集F，F={(xp,xq)|

xp≻xq,xp,xq∈X}，符号≻表示前者优于后者。根据决策原理，到各属性理想值欧几里德距离越小表示该方案越优，推广到群体决策中，如果xp≻xq并且有dp≤dq，则表示专家偏好符合一致性，表示为否则，表示专家偏好不符合一致性，用来表示：

并由此可推知群体群体决策一致度为G和群体不一致度为B：

根据上式可以推知:

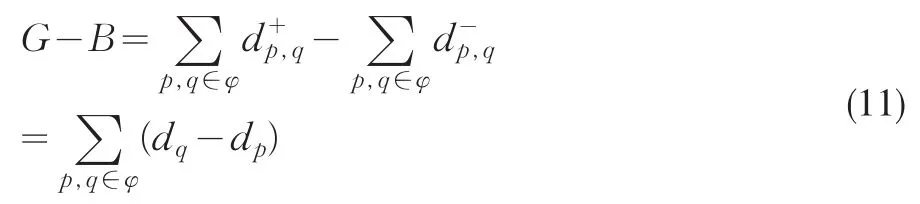
Step 4分析专家意见相互关系，确定分布函数，构造非线性目标函数。首先dp和dq关系分布函数如式（11）和式（12），分布如图1。

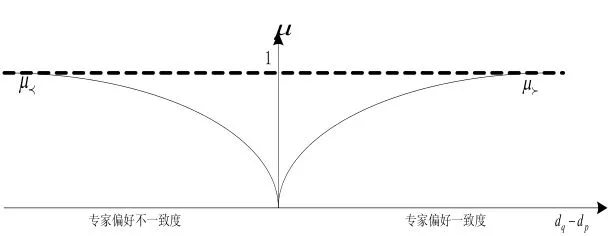
图1 专家偏好一致度函数分布

由于群体不一致度为B，则应满足ξ≺(B)尽可能小，同时又要使G-B尽可能大，令G-B最小差异为h，构造函数[11]：

式中h、k由决策者给定，为便于比较将函数η(G-B)分布置于[0,1]区间，可见函数满足单调性，要使η(G-B)尽可能大又使得ξ≺(B)尽可能小，即ξ≺(B)和1-η(G-B)均尽可能小，引入式中间变量λ,λ=max{ξ(B), 1-η(G-B)}.并根据分析构造目标函数如下：

Step 5解非线性方程组，得到属性权向量和理想方案属性值，并计算各备选方案到理想方案的关联系数，构建关联系数矩阵D=[ξij]n×m。将公式(6)关联关系拓展到多属性决策领域，计算各方案属性值与理想方案各属性的关联系数为ξij：

分辨系数ρ取值为0.05，使决策关联系数长度区间达到95%，已符合本文决策需求精度。针对决策属性uj来说，ξij越大说明备选方案与理想方案在该属性上越接近。Step 6计算各方案的综合关联度ζi，并进行决策。

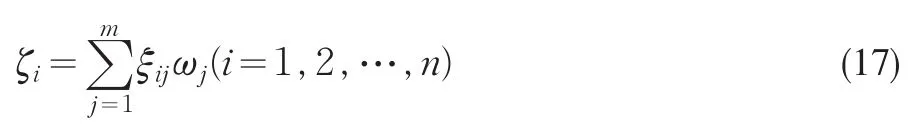
ζi表示备选方案到理想方案的综合相似程度，ζi越大表明备选方案与理想方案越相似，方案越优，反之，方案越差。

3 应用案例

表1 不同开发模式相关属性评价表

表2 语言变量三角模糊表示数

长株潭城市群发展中某大型基础设施项目运作模式决策中，初步研究分析可以采取A、B、C、D四种备选方案，为保证决策的科学合理性，必须对各备选方案对社会、经济、环境及资源利用等方面进行系统分析，组织专家对备选模式的社会经济、生态环境、资源利用和国民经济四方面进行评价，如表1所示，并得到专家偏好集合φ={(A,B),(A,D),(B,C),(B,D),(C,A),(D,C)}，运用多属性非线性决策模型进行决策。

确定语言变量三角模糊表示，如表2所示：

依据表1、表2构建决策矩阵A，并将矩阵A进行规范化，得到规范化矩阵R。

将R作为初始变量输入，令h=0.5,k=0.1,求解模型得到属性权重值和理想方案的属性值分别为：

W=（0.3560,0.1304,0.3206,0.1930），

A*=((0.5160,0.7180,0.9330）,(0.2046,0.2846,0.7673),(0.240,0.4242,0.6231),(0.1527,0.7681,0.7742))依据公式(16)计算各备选方案与理想方案属性的关联系数，构成关联系数矩阵如下：

根据公式(17)计算各备选方案的综合关联度，并进行决策。项目综合关联度分别为ζA=0.697，ζB=0.764，ζC=0.324，ζD=0.507，对综合关联度进行排序，即ζB＞ζA＞ζD＞ζC，方案的优劣秩序依次为B≻A≻D≻C。

4 结论

本文针对群体多属性决策中评价值具有模糊性和属性权重不确定的问题，提出了一种非线性规划求解属性权重和理想方案的方法，该方法是运用三角模糊向量距离比较与专家偏好可信度为基础，通过构建非线性规划模型，求解模型得到理想方案属性值和属性权重，然后依据备选方案与理想方案的综合灰色关联度进行方案的决策排序。该方法与传统的线性规划多属性规划方法比较具有决策参数少，简单易行的特点，并且该方法可以克服多维向量距离决策不唯一性，还可以防止GRA法主观偏好的影响，通过算例验证，决策结果比较理想。

[1]黄智力,李茂青.基于理想点的三角模糊数群体多属性决策法[J].厦门大学学报（自然科学版）,2008,47(11).

[2]龚艳冰.基于方案偏好和部分权重信息的模糊多属性决策[J].控制与决策,2008,23(5).

[3]杨静,邱菀华.基于投影技术的三角模糊数型多属性决策方法研究[J].控制与决策,2009,24(4).

[4]卫贵武,王小容.对方案有偏好的模糊多属性决策的GRA方法[J].系统工程与电子技术,2008,30(8).

[5]刘健,薛利,刘思峰等.基于优势关系的多属性决策问题研究[J].控制与决策,2010,(7).

[6]陈晓红,阳熹.一种基于三角模糊数的多属性群决策方法[J].系统工程与电子技术,2008,30(2).

[7]吕翔昊,李登峰.基于模糊信息的群体多维偏好分析决策模型[J].系统工程与电子技术,2004,26(5).

[8]李元东.基于模糊信息的多维偏好分析决策模型[J].西南师范大学学报（自然科学版）,2009,34(5).

[9]Sadoullah Ebrahimnejad,Seyed Meysam Mousavi,Hamed Seyrafin⁃pour.Risk Identification and Assessment for Build-Operate-Transfer Project:A Fuzzy Multi Attribute Decision Making Model[J].Expert Systems with Applications,2010,37.

[10]Li Dengfeng Extension of the LINMAP for Multi Attribute Decision Making under Atanassov’s Intuitionistic Fuzzy Environment[J].Fuzzy Optimization and Decision Making,2008,7(1).

[11]Amir Yousefli,Majeed Heydari,Kamram Shahanaghi.Development of Linear ProgrammingTechniqueforMultidimensionalAnalysis of Pref⁃erence in Fuzzy Environment[J].Journal of Uncertain Systems,2009,3(2).