轴向永磁轴承的设计与试验验证

2012-07-21张钢孙昌张坚张海龙蒋德得

轴承 2012年11期

张钢，孙昌，张坚，张海龙，蒋德得

(上海大学机电工程与自动化学院轴承研究所，上海 200072)

主动磁悬浮轴承是利用可控磁场力提供无接触支承，使转子稳定悬浮于空间且其动力学性能可由控制系统调节的一种新型高性能轴承，其研究涉及机械学、电磁学、电子学、转子动力学、控制理论和计算机科学。它是一种典型的机电一体化产品[1]，但造价过于昂贵，且需要专业技术水平很高的人员进行安装维护，因此在国内尚未能得到广泛应用。

永磁悬浮轴承(简称永磁轴承)是利用永磁体产生的磁场力将转子悬浮起来，不需要主动电子控制系统，减少了复杂电子控制器件可能失效的风险，系统也将更加可靠，使用寿命更长。永磁轴承作为被动磁悬浮轴承的一种[2]，目前虽然已在电表、风力发电机和永磁悬浮列车等特殊场合得到了某些应用，但它也是与机械支承相结合的。缺点是装配困难，需要资深专业技术人员安装维护，还不能普遍地应用到一般的工业机械中。因此，目前国内、外还没有像滚动轴承那样由专业厂家生产制造的标准化和系列化的永磁悬浮轴承。

由Earnshaw定律可知，永磁轴承不能实现所有自由度的稳定[3]。因此，在永磁悬浮系统中，至少在一个自由度上需要引入其他主动支承方式。本例基于轴向永磁悬浮技术方案提出了工业应用型轴向推力永磁轴承的设计思路。文中所述的工业应用型永磁轴承是指：将永磁悬浮轴承做得像滚动轴承那样便于安装和使用；并能在工厂中实现标准化、系列化生产；用户工程技术人员能像滚动轴承那样把它设计应用到主机产品中；其制造成本与滚动轴承相当，并能够像滚动轴承那样得到广泛应用[4]。

1 结构设计

轴向永磁轴承由轴向并行放置的永磁环构成，利用永磁体之间的作用力来实现悬浮物体在部分自由度上面的稳定悬浮，它不需要控制系统，悬浮功耗相对较小。文献[5]曾提出了在一定假设基础上建立适用于轴向磁化和径向磁化的磁环来设计磁轴承的通用模型。由于轴向磁化磁环在加工技术工艺上容易实现，本设计系基于轴向磁化的永磁环[6]。图1所示为轴向推力永磁轴承单元结构图。通过调整永磁环的轴向相对位置，可获得所需的轴向力。图中永磁环放置的相对位置可以获得最大的轴向力。

图1 轴向推力永磁单元结构图

在实际设计中，为了适应不同的工况，永磁轴承在结构上有很多选择，可以通过采用多对磁环叠加的方法来增加永磁轴承的刚度和承载力。图2是轴向永磁轴承结构示意图。它由轴圈、座圈、静永磁环、动永磁环、隔圈和保持轴承组成。永磁环材料选用N35型稀土钕铁硼，其参数为：Hc=1 038 kA/m，Br=1.191 T。

1—轴圈；2—座圈；3—静永磁环；4—动永磁环；5—隔圈；6—保持轴承

轴向推力永磁轴承的工作原理：上、下两座圈上的永磁环为静永磁环，轴圈上的永磁环为动永磁环；静永磁环磁极方向一致且与相邻动永磁环磁极方向相反。动/静永磁环之间的磁斥力使动磁环在受载时产生一个相反方向的恢复力，实现稳定悬浮。建立rz二维坐标系，如图3所示：r轴表示径向，z轴表示轴向。由于2个动永磁环之间为吸引力关系，所以可将2个动永磁环视为整体进行原理简化分析。当动永磁环在外载荷Fz的作用下向下移动z时，下间隙减小为c-z(c为平均间隙)，上间隙增加为c+z，使得下静永磁环对动永磁环向上的斥力Fz1大于上静永磁环对动永磁环向下的斥力Fz2，产生一个向上的恢复力Fz1-Fz2来承受外载荷Fz，实现稳定悬浮。

图3 动永磁环受力图

根据Newton第三定律，轴向外载荷Fz为

北京市召开节约用水大会。3月25日，2010年北京市节约用水大会在北京会议中心召开。会议总结了2009年北京市节水工作，部署了2010年工作任务，表彰了2009年度北京市节约用水先进单位、2009年度北京市节水系统先进集体和先进个人，并向全市中小学生代表发放了《北京之水》知识读本，并由北京市水务局与石景山、大兴等区县代表签署了节水目标责任书。

Fz=Fz1-Fz2，

(1)

保持轴承所受的作用力Fr为

Fr=Fr1+Fr2。

(2)

如果设计、加工和装配良好，保持轴承的径向间隙很小，动永磁环的径向位移也很小，保持轴承所受的力Fr就很小，它的摩擦阻力(矩)也非常小。

轴向刚度为

(3)

径向刚度为

(4)

2 磁力特性

为了求得轴向永磁轴承动磁环上的总磁力，需要对动磁环周围空气层的磁力进行求和。在有限元软件ANSYS中，用虚功方法计算磁力可以通过能量对可移动部件位移的微分得到，空气层单元轴线方向上磁力的基本表达式为

(5)

(6)

文献[3]研究了采用ANSYS分析轴向轴承轴向刚度的可行性。研究结果表明，在计算永磁轴承的承载能力时有限元法数值解与试验结果较吻合[7-10]。

本例采用ANSYS12.0软件，完成了轴向永磁轴承的承载能力分析。借助于ANSYS中关于电磁场的分析方法，选用SOLID98单元类型进行磁环完整建模，建模后进行网格划分，并给其施加Maxwell面标志和虚功位移边界条件，求解后可以得到动永磁环在组合磁场中的轴向力数值。对动/静永磁环间隙(轴向间隙)c分别为2，6，11和21 mm时的轴向力进行计算，并根据计算结果数据绘制动永磁环轴向力与轴向位移的关系曲线如图4所示。

图4 永磁轴承轴向力与轴向位移拟合曲线

从图4可以看出，轴向间隙越小，相同位移下的承载力就越大，轴向刚度也就越大。因此可以得出：c=2 mm时Kz≈169.02 N/mm；c=6 mm时Kz≈83.096 N/mm；c=11 mm时Kz≈39.480 N/mm；c=21 mm时Kz≈11.710 N/mm。理论轴向刚度为正则说明轴向可以稳定承载。

下面以轴向间隙2 mm为例，对动静永磁环进行ANSYS建模，研究动永磁环在一定范围的偏心距内变化时径向力所呈现的特性。具体数值见表1，对径向位移0 ～0.20 mm之间的数据进行曲线拟合(图5)。

表1 径向力随径向偏心距变化关系(c=2 mm)

图5 径向力随径向偏心距变化的拟合曲线

由图5可知，在较小的偏心距范围内，动永磁环在径向上受到静永磁环对它的径向斥力，而且斥力大小随着偏心距的增大而增大。动永磁环在径向上不会受到向轴线拉近的回复力，因此动永磁环不具有自动对心能力。

由图5可知：当c=2 mm时，径向刚度Kr≈-86.796 N/mm，径向刚度为负说明径向不稳定，必须加径向滑动保持轴承。

表1中当径向偏移量为0.5 mm时所对应的径向力约45 N，数值偏大，故实际设计中径向偏移量不宜过大，一般控制在0.05 mm以内，此时所对应的径向力约为4 N，降低了对径向保持轴承的压力，摩擦阻力非常小。

3 试验验证

为了测量轴向永磁轴承在轴向较大范围内的承载力Fz，选择摩擦因数非常小的滑动轴承作为保持轴承。

试验中对轴向永磁轴承施加轴向载荷，以测量其承载力和刚度。将轴向推力永磁轴承轴向放置，放上标称测量砝码。为了测得准确的数据，加工了与隔圈内、外径相等，厚度分别为2，3，5和10 mm规格的调整圈。调整圈分别安装在隔圈与座圈接触表面(图6)，以调整试验中最关键的磁环间隙。试验测量原理示意图如图7所示。

1—轴圈；2—座圈；3—静永磁环；4—动永磁环；5—隔圈；6—保持轴承c7—调整圈

图7 试验测量原理示意图

理论上可以测得磁环间隙从1～21 mm超过40组以上的数据。本例只测量了几组有代表性的间隙，分别为1，2，6，11和21 mm。值得注意的是，选择间隙为1 mm试验时，当承载力增加到一定数值时就会出现磁环触碰现象，所以出于安全性考虑不予选择。表2和表3分别列出动/静磁环之间的最大间隙21 mm以及最佳间隙2 mm时的测量数据。

表2 间隙21 mm时轴向永磁轴承试验数据

表3 间隙2 mm时轴向永磁轴承试验数据

由两组数据不难看出载荷与相对下垂位移之间的关系，由此便可得出轴承承载力与轴向位移(相对下垂位移)之间的关系。

调整永磁环间隙，最后得到如图8所示的力学特性试验曲线。

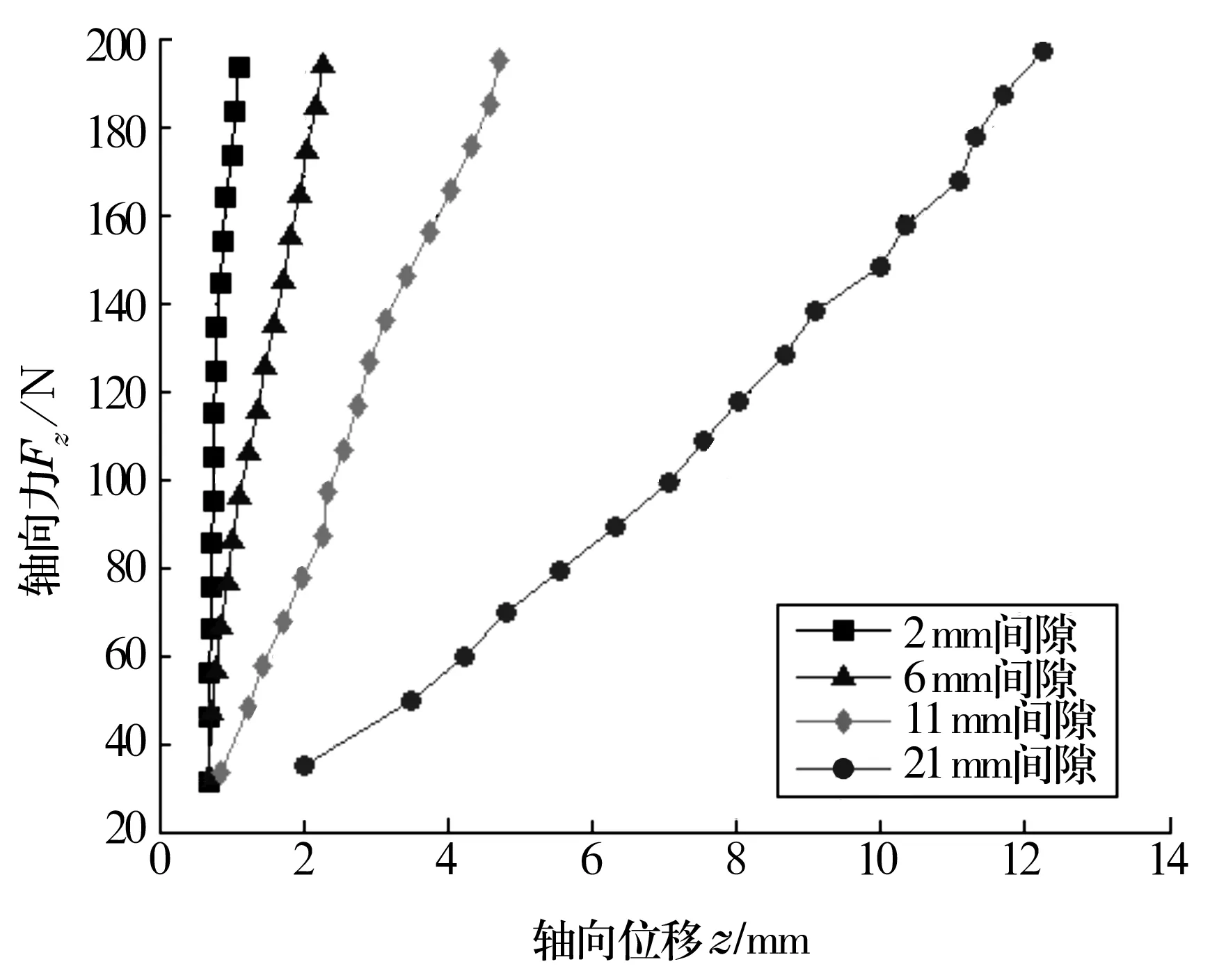
图8 轴向永磁轴承承载力与轴向位移曲线

对不同间隙下轴向永磁悬浮轴承轴向载荷与轴向位移试验值进行曲线拟合，由图8可以验证理论计算得出的结论，即轴向气隙越小，相同位移下的承载力就越大，轴向刚度也就越大。试验得到的轴承刚度为：c=2 mm时，Kz≈174.5 N/mm；c=6 mm时，Kz≈84.9 N/mm；c=11 mm时，Kz≈42 N/mm；c=21 mm时Kz≈15.5 N/mm。在轴向承载能力上，试验值与理论值最大偏差为3.24%。