内爆炸作用下地铁车站结构的动力响应与破坏分析

曲树盛，李忠献

(1. 天津大学建筑工程学院，天津 300072；2. 天津大学滨海土木工程结构与安全教育部重点实验室，天津 300072)

内爆炸作用下地铁车站结构的动力响应与破坏分析

曲树盛1,2，李忠献1,2

(1. 天津大学建筑工程学院，天津 300072；2. 天津大学滨海土木工程结构与安全教育部重点实验室，天津 300072)

地铁车站环境封闭，一旦其内部发生意外或恐怖爆炸事件，结构会在爆炸波的冲击作用下产生强烈的动力响应和局部破坏．采用数值方法对地铁车站在背包炸弹等中小型爆炸装置产生的内部爆炸作用下的结构动态响应进行了分析，得到了梁、板、柱等主要受力构件的位移和应变等动力响应，同时分析了炸药量、构件配筋率以及土-结构相互作用等因素对结构主要受力构件响应的影响．研究表明：在内部爆炸作用下，地铁车站的站台板是结构中破坏最为严重的构件，临近柱和中板会产生开裂等轻微破坏；结构的动力响应随炸药量的增大而增大，随构件配筋率的增大而减小；土-结构相互作用对于距离爆源最近的梁、板、柱构件响应影响较小．

地铁车站；内部爆炸；动力响应；结构破坏；数值分析

地铁作为缓解城市地面交通拥堵问题的一种有效途径，在许多国家得到了重视和发展．然而针对地铁的爆炸袭击事件在世界各地频繁发生，如巴黎(1995年，1996年)、伦敦(2005年)、莫斯科(2004年，2010年)、白俄罗斯(2011年)等，造成众多人员伤亡，以及列车和结构的破坏．由于地铁车站相对特殊的封闭环境，连续反射的爆炸波可能会引起结构的强烈响应、破坏甚至倒塌[1]，因此研究地铁车站内爆炸引起结构的非线性动力响应、破坏机理及防护措施具有重要的理论和现实意义．Lu等[2]对临近炸药爆炸作用下地下箱型结构的动力响应进行了研究；李忠献等[3]采用简化的爆炸荷载研究了单侧隧道内爆炸荷载作用下双线地铁隧道的动力响应，分析了土质、埋深和隧道间距等影响因素，并对泡沫铝加固的抗爆效果进行了研究；郭志昆等[4]对扁平箱形密闭结构内爆炸进行了模型试验研究，得到了结构的主要破坏形式；Hu等[5]分析了不同炸药量下地铁车站内结构柱的应力和位移响应，并未涉及梁、板等其他结构重要构件；廖维张等[6]研究了炸药位置和炸药量变化下地铁车站中柱的动力响应，得到结构的抗爆薄弱位置，但模型中没有考虑梁构件以及土-结构相互作用的影响．

笔者利用通用显式动力有限元分析程序ANSYS/LS-DYNA，采用 ALE(arbitrary Lagrangian Eulerian)方法[7]对地铁车站在内部爆炸作用下梁、板、柱等主要受力构件的动态响应和损伤破坏机理进行了研究，同时对炸药量、结构配筋率、土-结构相互作用等影响因素进行了分析，得到了地铁车站结构发生破坏的炸药 TNT当量阈值，并对结构抗爆设计提出了建议．

1 分析模型

1.1 工程背景

以天津地铁一号线某车站为依据，建立内部爆炸下地铁车站结构响应分析模型．车站横截面尺寸为20.4,m×12.7,m，采用现代典型的双层结构体系，地下一层为站厅层，净高为 4.5,m，地下二层为站台层，站台处净高4.8,m，轨道处净高6,m，站台宽11,m，车站内柱子的截面尺寸为800,mm×800,mm，纵向柱距8,m．

针对当前国际形势和地铁车站的特殊环境，考虑其遭受意外爆炸的装置主要是中小型爆炸装置如包裹炸弹和腰间炸弹，由于接触爆炸和近距离爆炸涉及到温度效应、冲击波绕射效应等多种因素的影响，目前采用数值方法尚不能得到较准确的结果，因此本文在分析时仅考虑了背包炸弹和腰间炸弹等距离地面较远的爆炸装置，根据这些装置的特点，结合国内外学者的建议[5-6]，本文将爆源位置定为站台候车区，距离地面中心典型高度 1.2,m处，考虑可能爆炸装置的等效 TNT当量为 0～20,kg．文献[8]研究表明，该地铁车站内爆炸波在传播至距离爆源28,m后爆炸荷载的超压和冲量都迅速衰减到可以忽略其对结构影响的程度，因此，在本研究中，仅建立了距离爆炸点28,m 范围内的车站结构模型．车站结构位于地面以下 3,m处，为考虑周围土体对结构响应的影响，建立炸药、空气、结构和土体的三维整体计算模型，土体环境的尺寸为 28,m×80,m×50,m．土与结构之间的相互作用采用的是 LS-DYNA中的接触算法进行模拟，该方法可以模拟土与结构之间的相互挤压、摩擦等效果；土体四周和底部的边界均采用了无反射边界条件，以消除应力波的反射，达到无限土体的模拟效果．车站结构的横截面如图1所示，构件编号见图2．

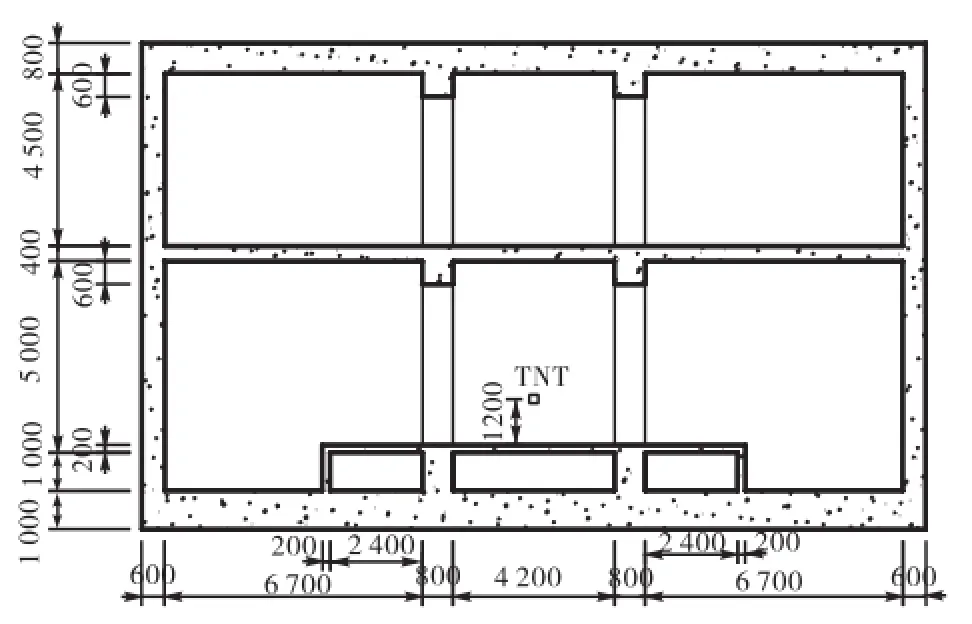
图1 模型横截面Fig.1 Cross section of the subway station structure

图2 结构主要构件编号Fig.2 Serial numbers of the key members

1.2 材料模型

1.2.1 空气

在数值模拟中，空气的材料模型假设为理想气体，其压力p和能量E1的关系为

式中：ρ为空气密度；E1为空气内能；k为空气绝热指数．在分析中，ρ取1.225×10-3g/cm3，k取1.4.

1.2.2 TNT炸药

TNT炸药的材料模型取为JWL状态方程．该状态方程可以用来计算爆炸中由化学能转化成的压力．压力与能量的关系为

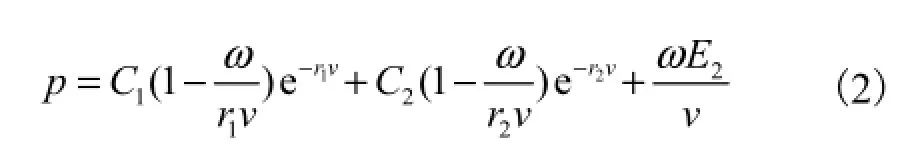
式中：v为炸药相对体积；E2为炸药内能；C1、r1、C2、r2和ω为材料常数．炸药TNT的材料参数可以假定为：C1=3.737,7×105,MPa，r1=4.15，C2=3.747,1× 103,MPa，r2=0.9，ω=0.35．

1.2.3 钢筋混凝土

LS-DYNA的材料库中包含多种可以模拟混凝土的动态力学模型[9]，Tu等[10]经过研究对比发现，这些混凝土模型中，MAT_CONCRETE_DAMAGE能够最有效地模拟钢筋混凝土在大变形、高应变率下的力学性态．同时，该模型可以通过参数设置钢筋的配筋率，在避免钢筋混凝土分离式建模的同时，较为准确地模拟钢筋混凝土在大变形、高应变率下的的动态力学性能．因此，本研究中采取 MAT_CONCRETE_ DAMAGE模型对钢筋混凝土结构进行建模，其主要参数如表1所示．

表1 钢筋混凝土材料模型的主要参数Tab.1 Main parameters of reinforced concrete model

在研究钢筋混凝土结构在爆炸冲击下的响应时须考虑钢筋和混凝土的应变率效应．材料的应变率效应通常用材料强度的动力增大系数(dynamic increase factor，DIF)来表示．本文中混凝土 DIF采用K&C模型，它是在CEB模型的基础上经过改进得到的[11-12]．混凝土抗拉强度动力增大系数表达式为

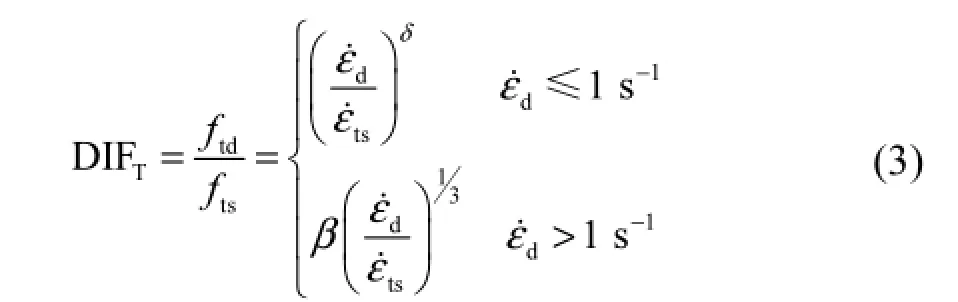
混凝土的抗压动力强度增大系数表达式为

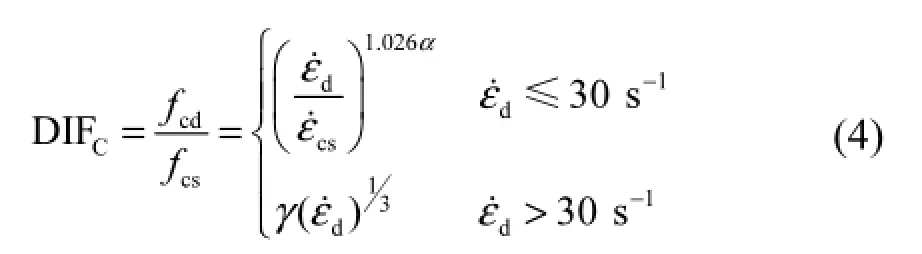
钢筋强度的DIF也是采用K&C模型[13]，即

1.2.4 土体

地铁车站整体位于地下，其结构在内部爆炸冲击下的响应会受到周围土体的影响．本文在研究过程中采用 Drucker-Prager模型[14]对土体的行为进行模拟．Drucker-Prager的屈服准则采用广义的von Mises屈服准则，考虑了静水压力对岩土材料的影响，其表达式为

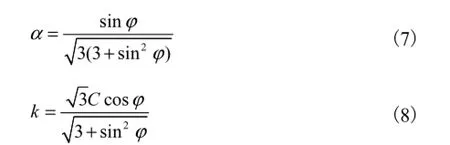
选用的土体模型(MAT_DRUCKER_PRAGER)的主要材料参数如表2所示．

表2 土的主要材料参数Tab.2 Main parameters of soil

2 计算结果分析与讨论

2.1 位移分析

利用LS-PREPOST对结构在内部20,kg TNT当量爆炸荷载作用下的响应与破坏进行了分析．结果表明，楼板、结构柱和连梁都发生明显的振动，如图3所示，典型位置节点的位移时程曲线如图 4所示，其位移响应的最大值如表3所示．

图3 t=71,ms时刻结构的位移响应Fig.3 Contours of resultant displacement at t=71,ms

从表3可以看出在爆炸荷载的冲击下，站台板的位移响应最为显著；从图 4可以看出，爆源正下方的节点z向最大位移达到23,mm，之后在结构阻尼的作用下站台板的振动逐渐衰减，并产生部分不可恢复的塑性变形；随着爆距 D的增大，爆炸波逐渐衰减，站台板上节点的位移响应峰值有减小的趋势．

图4 不同爆距处的站台板节点位移时程Fig.4 Time history of nodes displacement on platform at different distances from explosive

表3 结构中的位移最大值Tab.3 Maximum displacement of the members mm

2.2 应变及塑性变形

结构中的最大应变响应值如表4和表5所示．

表4 柱子的应变极值Tab.4 Extreme strain of columns 10-4

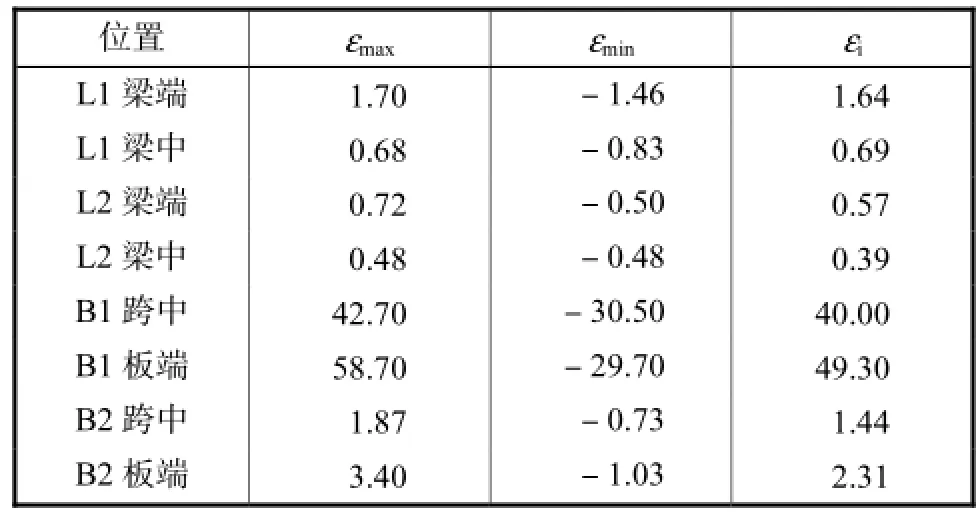
表5 梁、板的应变极值Tab.5 Extreme strain of beams and floors 10-4

从表4和表5中可以看出，较大的应变主要分布在站台板B1、结构柱C1和楼板B2上，其他构件应变值较小．混凝土开裂应变一般在 8×10-5至 2×10-4之间，以等效应变εi为依据，取混凝土开裂的极限拉应变为2×10-4，可以判断出混凝土可能发生开裂的构件有站台板B1、结构柱C1和楼板B2．

图5为结构在爆炸冲击作用下产生的塑性区域，在站台板跨中和板端的分布长度分别是 1.84,m 和3.76,m，该区域内的混凝土材料进入塑性后容易开裂形成碎块甚至脱落，从而造成结构的破坏．图 6为两段塑性区域内单元的等效塑性应变，从曲线中可以看出站台板的跨中位置首先出现塑性，经过3个阶段的塑性发展在 34.75,ms时达到最大值，并在之后保持为常数．板端出现塑性的时间稍晚，但发展很快，在29.49,ms时达到最大值，之后塑性应变保持为常数．同时，结构的其他构件都没有产生等效塑性应变，都处于弹性响应阶段．

图5 塑性区域Fig.5 Plastic zone

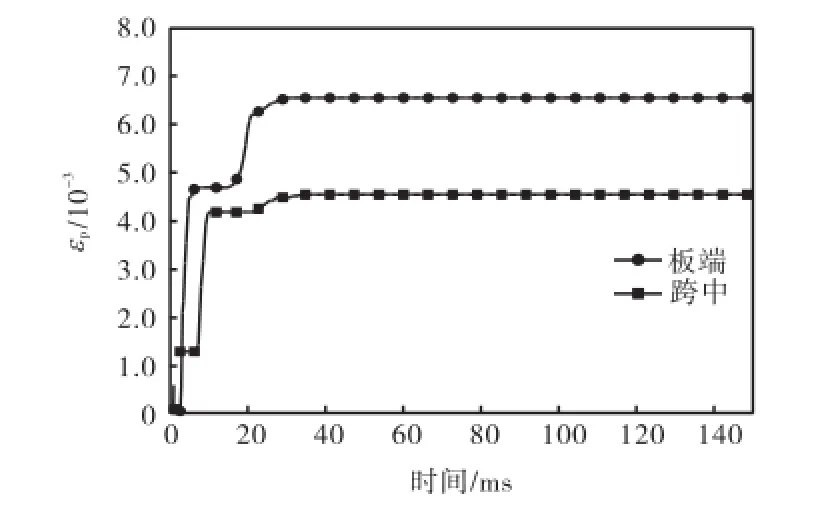
图6 站台板塑性应变发展Fig.6 Increase of effective plastic strain on platform floor

3 参数分析

3.1 药量分析

针对包裹炸弹等中小型爆炸装置，本节中考虑的炸药量分别为 5,kg、10,kg和20,kg．不同炸药量下结构的响应值如表 6所示．从表 6中可以看出结构的位移响应和应力响应都随炸药量的增大而增大．图 7为 C1柱底单元在不同炸药量下的应力时程对比，从中可以看出炸药量的不同直接影响到最大主应力的极值，在经历两个波峰后，不同炸药量下单元的应力差别不大，这是由于柱子从爆炸波中吸收的大部分能量，已经通过柱端传递到其他的结构构件．

图7 C1柱底最大主应力时程曲线Fig.7 Time history of maximum principal stress of column C1

从塑性区的发展来看，20,kg炸药量下站台板的跨中和板端都产生了较大的塑性区，10,kg炸药量下只有站台板的板端产生较小的塑性区，而在 5,kg炸药量下，结构中所有构件都没有塑性发展．可见，在本文所研究的爆源位置处发生 5,kg以下 TNT当量爆炸时，地铁车站结构不会发生破坏．

3.2 配筋率影响

为了研究配筋率对结构响应的影响，对5种不同配筋率的地铁车站结构内部发生 20,kg TNT炸药爆炸冲击下结构的响应进行分析，得到了部分关键位置处的节点位移和单元等效应变最大值，如表 7所示．在分析时为考虑钢筋的受拉破坏，取钢筋的极限拉应变为 1.0%，计算过程中当单元的最大拉应变超过该值时，即将其删除，表7中以“—”表示．

表7 不同配筋率下结构的响应最大值Tab.7 Maximum values of structure response at different reinforcement ratios

通过比较可以看出站台板的位移和等效应变响应值随着配筋率的减小而增大，在配筋率小于 1.0%时容易发生钢筋的拉断，因此建议在相关抗爆设计时考虑此最小配筋率的要求．对于地铁车站的其他构件，只有 C1柱底在配筋率为 0.2%时发生 5.08×10-4的等效塑性应变，其他构件均无塑性发展，动力响应值受配筋率的影响较小．

3.3 土-结构相互作用的影响

在内部爆炸冲击下车站结构会与周围土体发生挤压和滑移，为研究土与结构之间的相互作用对结构动力响应的影响，这里对比分析了考虑与不考虑土-结构相互作用，以及土取不同剪切强度时结构在内部爆炸作用下的动力响应，得到典型位置处的等效应力最大值如表8和表9所示．

表8 柱子的等效应力极值Tab.8 Extreme effective stress of columns MPa

表9 梁、板的等效应力极值Tab.9 Extreme effective stress of beams and floors MPa

从表8和表9中可以看出，不考虑地下结构周围土的影响时，距离爆源最近的柱C1、梁L1、板B1和B2的应力极值影响不大，变化范围在10%以内；随着构件与爆源距离的增大，周围土对构件应力响应极值的影响越来越大．因此在对地下结构内部某个单独构件进行抗爆性能研究时，可以不考虑周围土的影响，在对结构进行整体响应分析时必须考虑周围土的影响．土体的剪切模量会影响结构构件的动力响应，这种影响的规律性因构件类型和位置的不同而不同．

4 结 论

本文针对地铁车站遭受意外爆炸的主要爆源，通过对中小型爆炸装置在典型位置(如距离站台层地面中心点高度 1.2,m处)发生爆炸时的灾害进行模拟和分析，得到以下结论：

(1) 在20,kg TNT当量的爆炸作用下，站台板是破坏最严重的构件，在板端和跨中形成较大的塑性区域；距离爆源最近的结构柱和中板会发生混凝土的开裂等轻微破坏，其他距离爆源较远的结构构件均不会发生破坏．

(2) 结构的动力响应随炸药量的增大而增大；发生5,kg TNT当量以下的爆炸不会对结构造成破坏．

(3) 相同炸药量条件下，结构的动力响应随配筋率的增大而减小；常见中小型爆炸装置在典型位置爆炸情况下，当站台板配筋率小于 1.0%时容易发生钢筋的拉断，建议在相关抗爆设计时考虑此最小配筋率的要求．

(4) 土-结构相互作用对于距离爆源最近的梁、板、柱构件响应影响较小，可忽略其影响，对于距离爆源较远的构件影响较大．对地下结构内部某个单独构件进行抗爆性能研究时，可以不考虑周围土体的影响，在对结构进行整体响应分析时必须考虑周围土体的影响．

［1］ Li Zhongxian，Du Hao，Bao Chunxiao. Review of current researches on blast load effects of building structures in China[J]. Transactions of Tianjin University，2006，12(Suppl)：35-41.

［2］ Lu Yong，Wang Zhongqi，Chong Karen. A comparative study of buried structure in soil subjected to blast load using 2D and 3D numerical simulations[J]. Soil Dynamics and Earthquake Engineering，2005，25(4)：275-288.

［3］ 李忠献，刘 杨，田 力. 单侧隧道内爆炸荷载作用下双线地铁隧道的动力响应与抗爆分析[J]. 北京工业大学学报，2006，32(2)：173-181.

Li Zhongxian，Liu Yang，Tian Li. Dynamic responseand blast-resistance analysis of double tack subway tunnel subjected to blast loading within one side of tunnel[J]. Journal of Beijing University of Technology，2006，32(2)：173-181(in Chinese).

［4］ 郭志昆，宋锋良，刘 峰，等. 扁平箱形密闭结构内爆炸的模型试验[J]. 解放军理工大学学报：自然科学版，2008，9(4)：345-350.

Guo Zhikun，Song Fengliang，Liu Feng，et al. Experiment of closed flat box structure subjected to internal detonation[J]. Journal of PLA University of Science and Technology：Natural Science Edition，2008，9(4)：345-350(in Chinese).

［5］ Hu Qiuyun，Yu Haitao，Yuan Yong. Numerical simulation of dynamic response of an existing subway station subjected to internal blast loading[J]. Transactions of Tianjin University，2008，14(Suppl)：563-568.

［6］ 廖维张，杜修力. 内部爆炸作用下地铁车站的动力响应分析[J]. 地下空间与工程学报，2010，6(5)：980-985.

Liao Weizhang，Du Xiuli. Dynamic responses of subway station under the internal blast loads[J]. Chinese Journal of Underground Space and Engineering，2010，6(5)：980-985(in Chinese).

［7］ LS-DYNA. Theory Manual[M]. Livermore，California：Livermore Software Technology Corporation，2006.

［8］ 曲树盛，李忠献. 地铁车站内爆炸波的传播规律与超压荷载[J]. 工程力学，2010，27(9)：240-247.

Qu Shusheng，Li Zhongxian. Propagation law and overpressure load of blast wave inside subway station[J]. Engineering Mechanics，2010，27(9)：240-247(in Chinese).

［9］ LS-DYNA. Keyword User's Manual[M]. Livermore，California：Livermore Software Technology Corporation，2006.

［10］ Tu Zhengguo，Lu Yong. Evaluation of typical concrete material model used in hydro codes for high dynamic response simulations[J]. International Journal of Impact Engineering，2009，36(1)：132-146.

［11］ Malvar L J，Ross C A. Review of strain rate effects for concrete in tension[J]. ACI Materials Journal，1999，96(5)：614-616.

［12］ Comit E Euro-International Du B Eton. CEB-FIP Model Code 1990[S]. Trowbridge，Wiltshire，UK：Redwood Books，1993.

［13］ Malvar L J. Review of static and dynamic properties of steel reinforcing bars[J]. ACI Materials Journal，1998，95(5)：609-616.

［14］ 龚晓南. 土塑性力学[M]. 杭州：浙江大学出版社，1997.

Gong Xiaonan. Soil Plasticity[M]. Hangzhou：Zhejiang University Press，1997(in Chinese).

Dynamic Response and Damage Analysis of a Subway Station Structure due to Internal Explosion

QU Shu-sheng1,2，LI Zhong-xian1,2
(1. School of Civil Engineering，Tianjin University，Tianjin 300072，China；2. Key Laboratory of Coast Civil Structure Safety of Ministry of Education，Tianjin University，Tianjin 300072，China)

Strong dynamic responses and local damages might occur in the subway station structure once an accidental or a terrorist explosion happens internally due to its enclosed environment. The responses of a subway station structure to internal explosions from typical small explosive devices，such as suitcase bombs，were simulated. The dynamic displacement and strain of typical columns，beams and floors were derived for estimating the safety of the structure. Parametric studies were also carried out to investigate the influences of TNT equivalent charge weight，reinforcement ratio of concrete members and soil-structure dynamic interaction on the dynamic responses of the structural members. The results showed that the platform floor was the most seriously damaged member under the internal explosion，while minor damage such as small cracks might occur in the members near the explosion. Dynamic responses of the structure would get stronger with the increase of the TNT equivalent charge weight，and weaker with the increase of reinforcement ratio. The soil-structure dynamic interaction need not be considered since it had little effect on the dynamic response of the members near the explosion.

subway station；internal explosion；dynamic response；structural damage；numerical analysis

TU375

A

0493-2137(2012)04-0285-07

2011-08-24；

2011-10-20.

国家自然科学基金重点资助项目(50638030)；“十一五”国家科技支撑计划重点资助项目(2006BAJ13B02)；天津市应用基础和前沿技术研究计划重点资助项目(08JCZDJC19500).

曲树盛（1983— ），男，博士研究生，qushusheng@tju.edu.cn.

李忠献，zxli@tju.edu.cn.