基于有限元的舰船推进轴系合理校中计算方法

周 瑞

中国舰船研究设计中心，上海201108

基于有限元的舰船推进轴系合理校中计算方法

周 瑞

中国舰船研究设计中心，上海201108

推进轴系的合理校中直接关系到舰船推进系统运行和舰船航行的安全性与可靠性，因此，其计算方法的合理性和准确性是推进系统研究的重要内容之一。基于有限元分析，建立了舰船推进轴系合理校中计算模型，并计入了螺旋桨水动力、齿轮动态啮合力、轴承刚度、轴承变位、轴段剪切变形以及运行温度等因素对推进轴系校中的影响。以某型舰船的推进轴系为研究对象，采用所提出的方法进行了推进轴系冷态、热态以及安装状态的合理校中计算分析，并与Kamewa公司采用Shaft Analysis AB软件的计算结果进行了比对，平均计算偏差小于1.54%。

推进轴系；校中；有限元分析

0 引 言

推进轴系是舰船推进系统的重要组成部分，其运行状态取决于轴系的设计、制造和安装，同时又影响到舰船推进系统运行和舰船航行的安全性与可靠性［1］。轴系校中计算分为冷态校中计算和热态校中计算两种，其中冷态校中计算主要用于指导轴系的安装和检验，热态校中计算则是轴系安全运行的保障。合理的轴系校中应该是冷、热态兼优的结果，即各轴承负载均衡、各截面应力分布合理、轴系挠度及转角控制优良。实践证明，校中不良的轴系在运转时会造成轴承迅速磨损，甚至是造成摩擦副烧结，以及尾管密封元件异常磨损而导致泄漏、船体尾部振动加剧等［2］。

目前，国内外关于推进轴系校中常用的计算方法有3种，即传递矩阵法、三弯矩法和有限元法。传递矩阵法编程简单、运算速度快，但存在适用性差、数值计算结果容易产生不稳定等问题［3-5］。三弯矩法的计算精度高、适用性强，但计算量偏大，并且当需要计入外加力偶、线性均布载荷及轴段剪切变形时，需要对其进行改进，且编程复杂［6-7］。有限元法作为近年来兴起的一种计算方法，可以在船舶轴系校中计算中方便地计入更多影响因素，使得计算模型更接近船舶轴系实际运转时的状态，从而得到更加准确的计算结果。因此，有限元法在船舶推进轴系校中计算中得到了广泛的应用和发展［8］。

本文将给出一种基于有限元的推进轴系合理校中计算方法，在计算模型中计入螺旋桨水动力、齿轮动态啮合力、轴承刚度、轴承变位、轴段剪切变形及运行温度等因素的影响。运用Matlab编制计算程序，对某型舰船推进轴系进行了冷态、热态以及安装状态校中计算，并与Kamewa公司采用Shaft Analysis AB软件的计算结果进行比对分析。

1 有限元法轴系校中计算

1.1 梁单元刚度矩阵

进行船舶推进轴系弹性校中计算时，轴系通常简化为一个多支承的变截面连续梁系统，承受横向载荷和弯曲力矩的作用。对于任意平面梁单元，有限元计算模型如图1所示，当计入剪切变形影响时，平面梁单元的刚度矩阵为［9］：

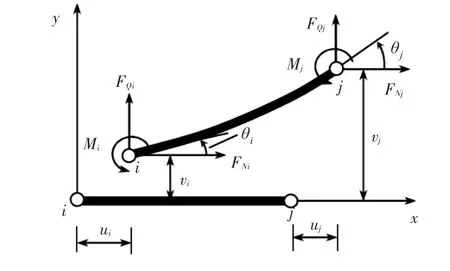
图1 平面梁单元受力模型Fig.1 Mechanical model of plane beam element

1.2 结点力向量

推进轴系校中计算有限元模型中的结点力向量由分布力（矩）的等效结点力和结点上的集中力（矩）两部分组成。作用在轴系上的分布力（矩）包括分布横向力、分布弯曲力矩和分布扭矩等，这些非结点载荷可以按照虚功相等的原则等效转换到分配到单元结点上的力上，其计算公式参见文献［10］。作用在结点上的集中力（矩）包括集中质量、集中弯矩和轴承支承变位产生的弹性力，其中轴承支承变位产生的弹性力为：

式中，KB为轴承支承的刚度值；δ为轴承支承的变位值。

1.3 坐标变换

推导梁单元刚度矩阵和计算分布力（矩）的等效结点力时，采用的是局部坐标系，坐标轴方向由梁的截面主方向确定。但是，轴系的实际结构可能由具有不同方向和处于不同位置的梁单元构成，其整体刚度矩阵和结点力向量不能由局部坐标下的矩阵简单地叠加生成，因此，必须建立一个统一的整体坐标系。

假设整体坐标轴 x－y与局部坐标轴 x′－y′相交成α角，如图2所示。计算时，首先将单元上的结点力和位移转换到整体坐标系，单元刚度矩阵亦作坐标变换，然后才可按照叠加规则直接相加组成整体刚度矩阵。对于平面梁单元，其刚度矩阵和等效结点力的转换矩阵为：

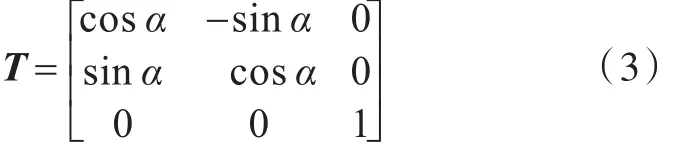
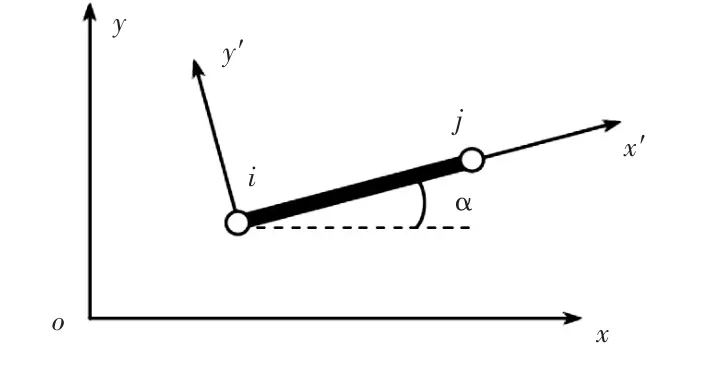
图2 整体和局部坐标轴位置Fig.2 Global and local coordinate axes

1.4 生成整体刚度矩阵和整体结点力列阵

整体刚度矩阵K由平面梁单元刚度矩阵和轴承支承单元刚度矩阵两部分组成。将平面梁单元的4阶刚度矩阵 KL加以扩大，写成2n×2n的方阵：

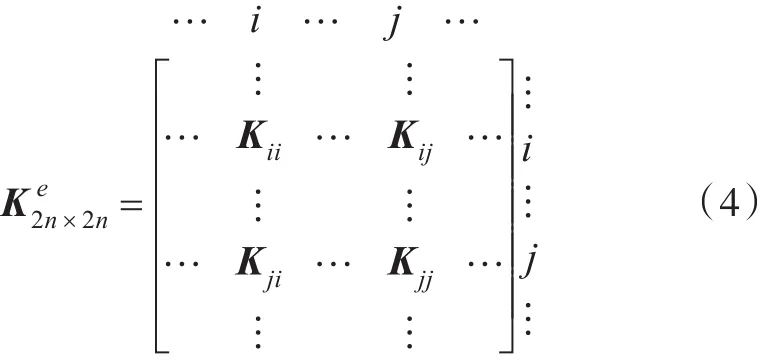
式中，n为结点数；虚点和空处的元素为2×2的零矩阵；i和j表示分块意义下子矩阵Kij等所在的行和列（实际上是两行两列），i和j的顺序按照结点编号从小到大排列。

通过将所有平面梁单元刚度矩阵KL中的4个子矩阵按其单元结点编号在式（4）的格式中进行对号叠加，即可得到刚度矩阵K′。

进行推进轴系弹性校中计算时，轴承接地端受到约束，轴承支承简化为一维单结点弹簧单元，将KB按轴承支承单元的结点编号在K′中进行对号叠加，即可得到整体刚度矩阵K。

同样，假设各单元结点力向量为 fi，将结点力向量加以扩大，写成2n×1阶的列阵：

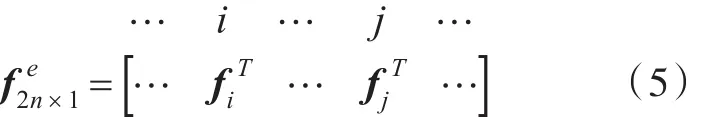
之后，按照有限元叠加规则直接相加，即可得到整体结点力列阵f。

例如，在学习人教版初中音乐《汉族民歌》时，教师可以结合教材需要进行对课堂改革，引导学生在课堂上学唱江苏民歌和中国民歌《茉莉花》，尝试同时演唱两种曲调不同的《茉莉花》，提高学生的学习积极性，教导学生两首歌的特点，同时针对其中民族文化进行教育，培养学生对祖国民族音乐的热爱和对祖国对家乡的情感，促进学生综合素养的教育培养。

1.5 求解系统方程

假设轴系被离散成ne个平面梁单元和n个单元结点，则整体结点位移列阵δ为：

因此，可得到系统方程为：

式中，整体刚度矩阵K为奇异矩阵，不能直接求解。在轴系校中计算有限元模型中，每个节点有两个自由度，当某个节点的某个自由度受到约束时，假设该自由度在整体结点位移列阵中的位置为i，则将K中的元素Kii置为1，第i行和第i列的其它元素置为零，整体结点力列阵中相应的元素fi＝β（β为该自由度的约束值），即可采用“划行划列法”进行求解。

引入约束条件后的系统方程变为：

式中，Ke和 fe分别为经过划行划列处理后的剩余矩阵。

求解方程（8）可得到整体结点位移列阵δ，进而求出各结点处的位移、转角、剪力和弯矩，以及各轴承支承的支反力。

2 计算程序流程图

基于上述轴系校中计算的有限元方法，在Matlab软件环境下利用M语言编制了轴系校中计算软件，其程序流程如图3所示。

图3 计算程序流程图Fig.3 Flow chart of the developed software

3 算例分析

以某型船的轴系为研究对象，计算轴系在冷态、热态以及安装工况条件下的校中结果。该套轴系全长31.5 m，分别由推进器轴、尾轴和中间轴组成，共布置6个轴承，包括3只水润滑轴承和3只油润滑轴承，如图4所示。推进轴系首端与齿轮箱大齿轮输出端相连，额定工况下的螺旋桨转速约为270 r/min，推力约为275 kN。

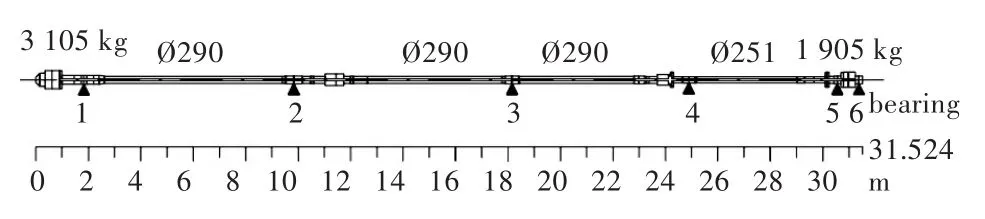
图4 推进轴系布置示意图Fig.4 Layout of the propulsion shafting

3.1 冷态校中计算结果

冷态工况下推进轴系校中计算计及了轴承变位、轴承支承刚度和轴段剪切变形的影响，计算结果如图5所示，图中给出了轴系上各截面处的挠度、转角、剪力以及弯矩的数值结果。

表1列出了冷态工况下各轴承负荷的计算结果，为了对比，将Kamewa公司采用Shaft Analysis AB轴系校中计算软件计算得到的结果同时列于表1。由表1可看出，采用本文计算程序得到的冷态工况下的轴承负荷计算结果与Kamewa公司给出的结果一致性良好。

图5 推进轴系冷态校中计算结果Fig.5 Shaft alignment calculation results in cold state

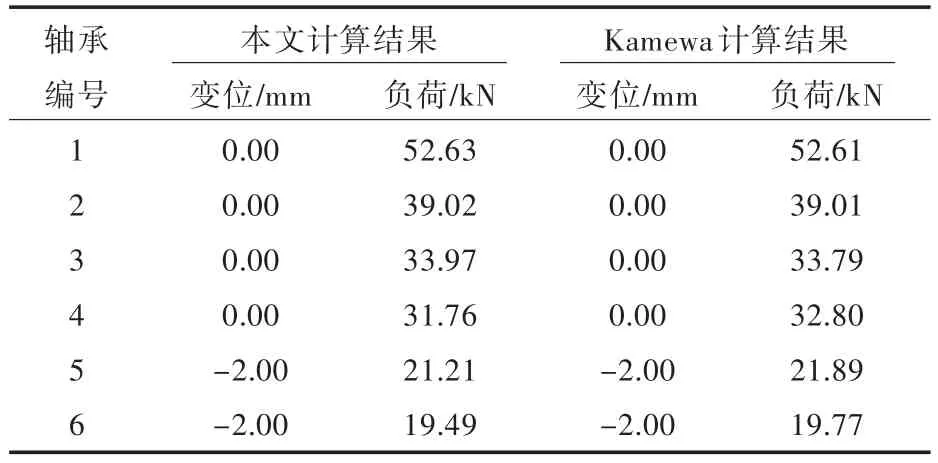
表1 冷态校中计算结果对比Tab.1 Comparison of calculation results in cold state

3.2 热态校中计算结果

热态工况下的校中计算除了计及冷态工况下的影响因素以外，还需考虑螺旋桨水动力、齿轮动态啮合力以及运行温度造成的支承膨胀变位等因素的影响。在热态工况下，推进轴系在垂直和水平方向上各截面处的挠度、转角、剪力以及弯矩的数值计算结果如图6所示。

表2列出了在热态工况下各轴承负荷的计算结果，Kamewa公司的计算结果也同时列于表2。由表2可看出，在热态工况下，采用本文计算程序得到的垂直与水平方向上的轴承负荷计算结果与Kamewa相应的计算结果均保持了良好的一致性，误差很小。

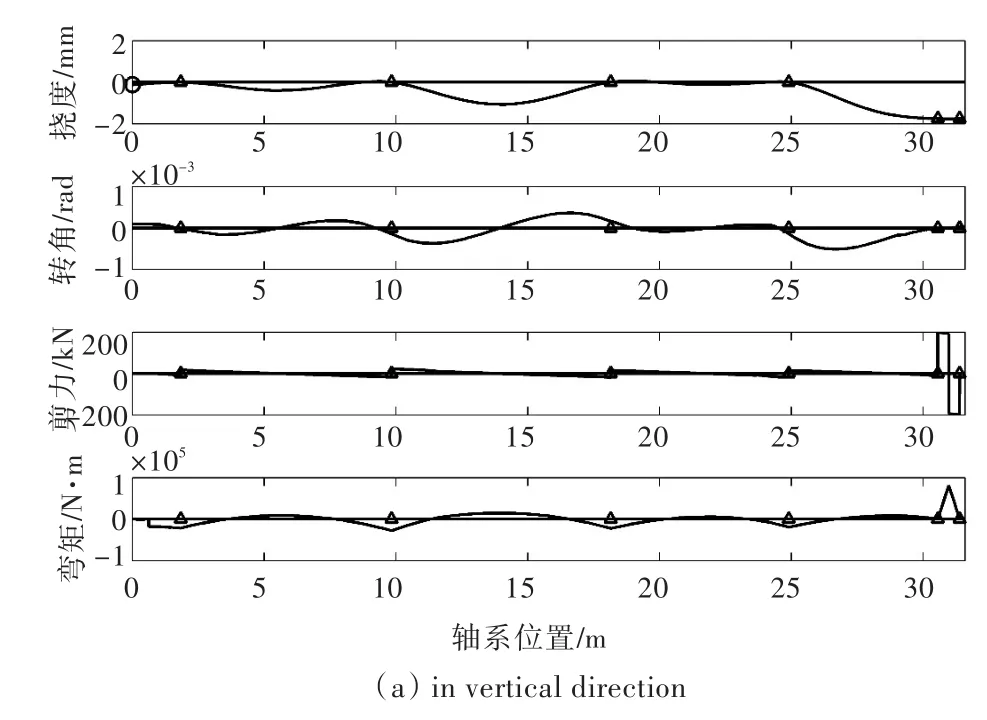
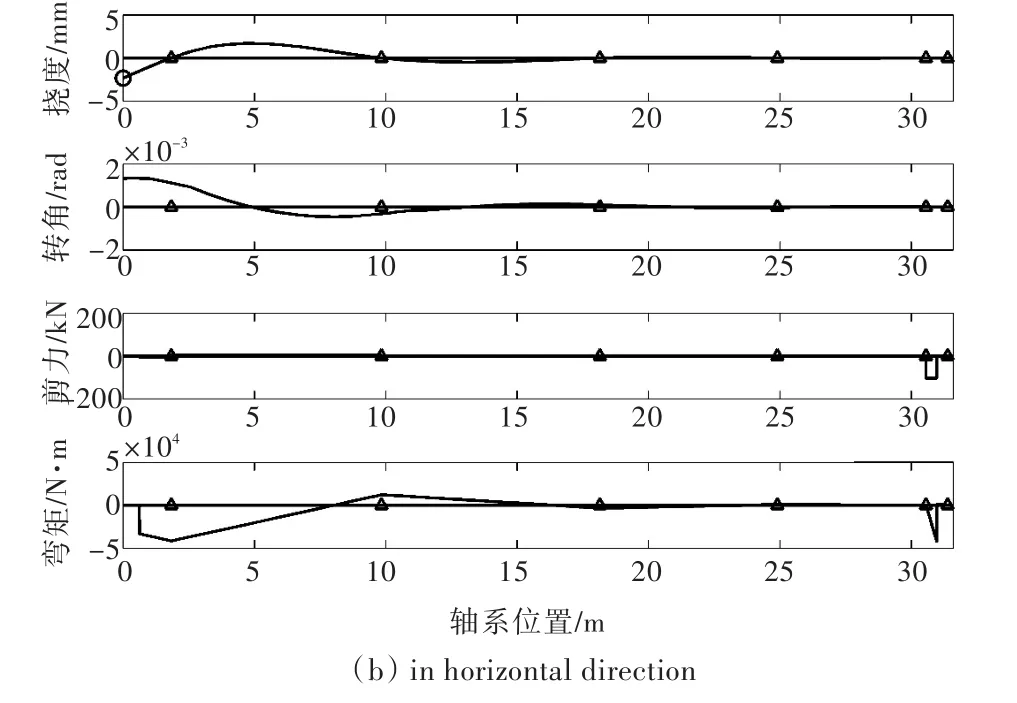
图6 推进轴系热态校中计算结果Fig.6 Shaft alignment calculation results in warm state

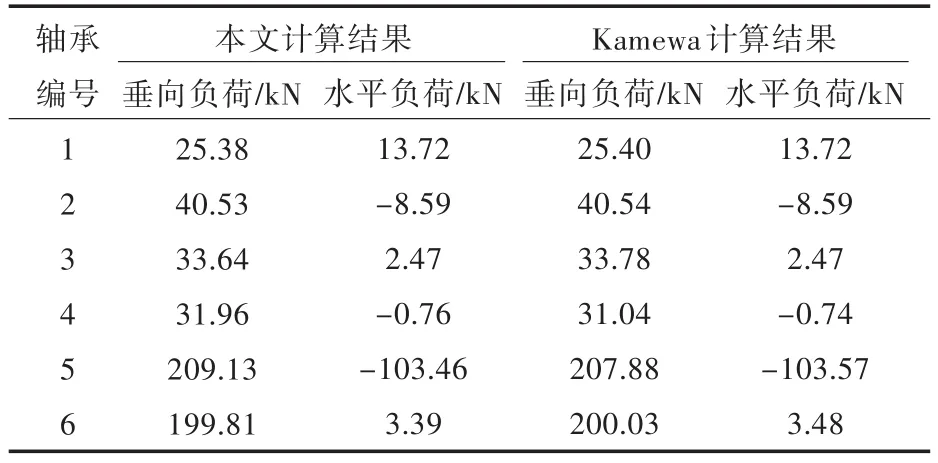
表2 热态校中计算结果对比Tab.2 Comparison of calculation results in warm state

3.3 安装状态计算结果

推进轴系在安装状态的挠度曲线如图7所示。从图中可看出，整个轴系分为3段，同时，为了实现对中以及安装方便，增加了两个临时辅助支承（T1和T2）。在安装状态下，各轴承以及两个临时辅助支承的负荷如表3所示，轴系两个连接端面位置处（图7中椭圆标记处）的开口和偏移的计算结果如表4所示。同样，Kamewa的计算结果也列于相应的表格中。

分别对比表3和表4可以看出，在安装状态下，推进轴系采用本文计算程序得到的各轴承支承和临时辅助支承的负荷以及两个轴系连接端面位置处开口和偏移值的计算结果均与Kamewa公司提供的计算结果保持了很小的误差。

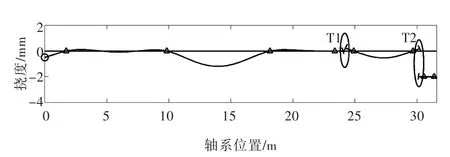
图7 轴系安装状态挠度曲线Fig.7 Shaftline deflection curve in open shafting state

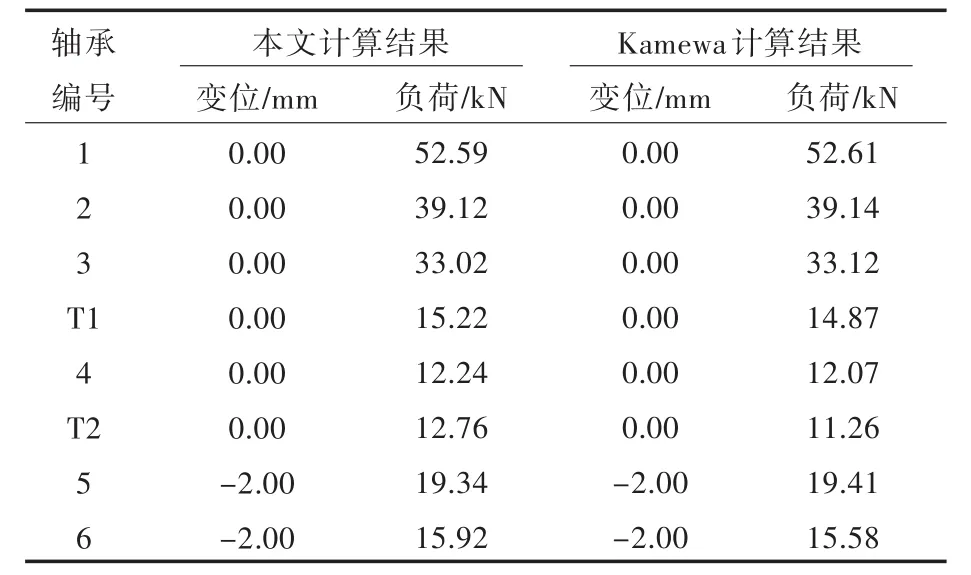
表3 安装状态轴承负荷计算结果对比Tab.3 Comparison of bearing load in open shafting state

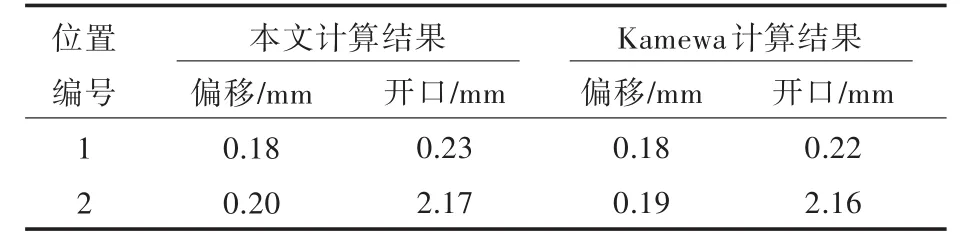
表4 安装状态开口、偏移计算结果对比Tab.4 Comparison of gap and sag in open shafting state

4 结 语

本文给出了一种基于有限元的舰船推进轴系合理校中计算方法，所建立的模型能够计入螺旋桨水动力、齿轮动态啮合力、轴承刚度、轴承变位、轴段剪切变形等多种因素对校中状态的影响，更加逼近轴系实际运行的物理模型。基于Matlab环境编制了计算程序，并以某型舰船推进轴系为研究对象进行了冷态工况、热态工况以及安装状态下的轴系校中计算，3个工况下的计算结果与Ka⁃mewa计算结果的偏差分别为1.42%，0.68%和2.29%，平均计算偏差小于1.54%，验证了所提方法的正确性和所开发软件的计算精度。

［1］周继良，邹鸿钧.船舶轴系校中原理及应用［M］.北京：人民交通出版社，1985.

［2］周瑞平，徐立华，张昇平，等.船舶推进轴系校中若干技术问题研究［J］.船舶工程，2004，26（6）：48-52.

ZHOU R P，XU L H，ZHANG S P，et al.Study on some technical problems in alignment of ship propulsion shafting［J］.Ship Engineering，2004，26（6）：48-52.

［3］魏海军，王宏志.船舶轴系校中多支承问题的研究［J］.船舶力学，2001，5（1）：49-54.

WEI H J，WANG H Z.Study on multi-bearings of ship⁃ping shaft system alignment［J］.Journal of Ship Me⁃chanics，2001，5（1）：49-54.

［4］王宏志，魏海军，关德林，等.中间轴承对船舶轴系力学状态影响的数字模拟［J］.船舶力学，2006，10（1）：98-105.

WANG H Z，WEI H J，GUAN D L，et al.Numerical simulation on ship shafting mechanics condition of in⁃termediate bearing［J］.Journal of Ship Mechanics，2006，10（1）：98-105.

［5］张洪田.船舶轴系合理校中技术研究［J］.黑龙江工程学院学报，2003，17（4）：3-7.

ZHANG H T.Research on alignment technique for ma⁃rine shafting［J］.Journal of Heilongjiang Institute of Technology，2003，17（4）：3-7.

［6］周瑞平，张昇平，杨建国.三弯矩方程的改进及在船舶轴系动态校中中的应用［J］.船舶工程，2003，25（1）：40-43.

ZHOU R P，ZHANG S P，YANG J G.Application of im⁃proved three-moment equation in dynamic alignment of ship shafting［J］.Ship Engineering，2003，25（1）：40-43.

［7］周瑞平.超大型船舶推进轴系校中理论研究［D］.武汉：武汉理工大学，2005.

ZHOU R P.The Theoretic studies on the propulsion shafting alignment of ultra-large vessels［D］.Wuhan：Wuhan University of Technology，2005.

［8］耿厚才，饶柱石，崔升.船舶轴系油膜计算与轴承反力分析［J］.船舶力学，2004，8（5）：120-124.

GENG H C，RAO Z S，CUI S.Oil film calculations and reaction analyses for marine shaft system［J］.Journal of Ship Mechanics，2004，8（5）：120-124.

［9］ZHOU R P，XU L J，LI B R，et al.Improvement of fi⁃nite element analysis in the propulsion shaft alignment［J］.Journal of Ship Mechanics，2005，9（3）：111-117.

［10］徐荣桥.结构分析的有限元法与MATLAB程序设计［M］.北京：人民交通出版社，2006.

Calculation Method for Ship Propulsion Shafting Alignment Based on Finite Element Analysis

ZHOU Rui

Shanghai Division，China Ship Development and Design Center，Shanghai 201108，China

The propulsion shafting alignment directly affects the security and reliability of the propulsion system operation and the ship navigation，the rationality and accuracy of the alignment calculation method is important for propulsion system.In this paper，a propulsion shafting alignment method based on finite el⁃ement analysis was proposed.The proposed method investigated the factors such as propeller hydrodynam⁃ic force，gear dynamic meshing force，bearing stiffness，bearing displacement，shear deformation for the shafting and operation temperature.The alignment analysis was respectively performed under cold state，warm state and installation state for a propulsion shafting.The results of proposed method agree well with the calculation results of Shaft Analysis AB software in the same conditions，and the mean calculation er⁃ror is less than 1.54%.

propulsion shafting；alignment；finite element analysis

U664.2

A

1673－3185（2012）03－74－05

10.3969/j.issn.1673－3185.2012.03.014

2011－12－22

国家部委基金资助项目

周 瑞（1980－），男，博士，工程师。研究方向：船舶动力系统。E⁃mail：hit_zhourui＠163.com

周 瑞。

［责任编辑：喻 菁］