某型履带式运输车扭杆悬挂装置力学性能分析与优化*

2012-07-19魏小强

汽车工程 2012年1期

魏小强，成凯，林源

(1.吉林大学机械科学与工程学院，长春 130025;2.长春职业技术学院，长春 130033)

前言

某铰接履带式运输车由前后两个车体组成，车体中间通过铰接支架连接。其车体通过扭杆悬挂装置支撑整车的质量，履带缠绕在主动轮、诱导轮和负重轮上，履带和地面接触，负重轮在履带的夹道上运动，发动机动力经传动系传递到前后车的主动轮，再经履带带动整车运动。扭杆悬挂装置的强度和刚度对车辆使用极为重要［1］，利用公式和有限元理论对其强度和刚度进行了分析。并对扭杆悬挂装置的平衡肘结构进行了拓扑优化，分析结果为该车结构设计提供了可靠依据。某铰接履带式运输车外观模型如图1所示。

1 扭杆悬挂装置的三维实体模型

某铰接履带式运输车的扭杆悬挂装置如图2和图3所示，它由平衡肘、套筒、扭杆、扭杆护罩和限位块等组成，平衡肘和负重轮轴采用一体锻造，负重轮为可充气轮胎。扭杆上面的护罩焊接在车架底板上。两个扭杆中间分开，是单独的一套装置;平衡肘和套筒是焊接的，可认为两者是固结的。套筒有花键槽，扭杆上带有花键，一端焊接在车体上，另一端和套筒通过花键连接，平衡肘转动时带动扭杆受扭。

对扭杆悬挂装置各部分均采用Pro/E建立模型，花键和限位器采用简化装置，几何模型中不包含这两部分。前后车的扭杆悬挂装置一样，取出其中一个装置进行有限元校核。

扭杆悬挂装置的设计应满足力学性能要求，具备足够的强度和一定的柔度，既能可靠地传递车身自重和载重，又具有良好的行驶平顺性和减振性能，并在转向、制动和俯仰动作时操作平稳，保持车身稳定。此外，还应满足部件质量轻、寿命长的要求。

2 扭杆悬挂装置的有限元模型

2.1 模型中的重要单元

(1)杆单元LINK10

LINK10单元有双线性刚度矩阵特性，使其成为一个轴向仅受拉或仅受压的杆单元。使用只受拉选项时，如果单元受压，刚度就消失，以此来模拟缆索或链条的松弛。

(2)非线性弹簧单元COMBIN39

须要定义COMBIN39单元的实常数，指定任意过原点的曲线或折线，作为广义的力－变形曲线，但要求过原点在第一象限的小段曲线斜率为正值。该单元可用于任何分析之中。在一维、二维和三维的应用中，单元都有轴向承载或扭转功能。轴向选项代表轴向拉压单元，每个节点具有沿节点坐标系X、Y、Z 3个轴的平动自由度，不考虑弯曲和扭转。扭转选项代表纯扭单元，每个节点具有绕节点坐标轴X、Y、Z 3个轴的转动自由度，不考虑弯曲和轴向荷载。此单元仅当每个节点有两个或者3个自由度时，才可具有大位移的功能。

2.2 模型信息和约束加载

该模型计算时只针对平衡肘进行校核，上面的几何模型全部按照实体固结处理，采用SOLID185和SOLID73两种实体单元。扭杆悬挂装置组装模型对扭杆强度不做校核，另有单独计算。

采用网格划分软件对几何模型进行几何修补、拓扑连接处理、网格划分和单元信息添加等，最后形成有限元模型。节点总数是17 871个，单元总数是64 197个，其中实体单元63 879个，弹簧单元1个，杆单元83个，辅助单元234个。

扭杆端部一圈节点约束3个方向的平动，在套筒和扭杆利用花键连接的部位取一个截面，在截面内建立一圈沿轴向分布的单元，X轴朝向圆心的杆LINK10，设置其关键字keyopt(3)=1，指定仅能承受压力，约束杆的端部3个自由度，来模拟套筒对扭杆的支撑作用。并在杆与实体连接处加一圈辅助梁，使杆单元单点承压力分散，降低此处的应力。

限位器固定在车身上，当负重轮受到地面不平度影响而上下起伏时，平衡肘和负重轮一起绕扭杆轴线旋转，当旋转至最大垂直位移为144mm(此值是通过车体水平放置时的结构尺寸计算得到的)时，与平衡肘相连的限位块与车身的限位器接触，由于限位器的强度足够大，平衡肘被卡紧不再绕扭杆轴线旋转，起到保护车体稳定运行的目的。采用弹簧单元COMBIN39来模拟限位器，其特性数据见表1。

表1 弹簧特性数据

弹簧单元上端固定不动，当垂直位移不到144mm时，弹簧力很小，仅为0.1N，当垂直位移等于或超过该值时，弹簧力为50kN，此力足够大，可防止平衡肘的旋转。

在弹簧上面和车体上伸出的圆筒板连接处施加全部约束，连接在平衡肘上的实体块和弹簧连接处用辅助梁BEAM188单元局部加强。

扭杆悬挂装置的材料和力学性能见表2，表中拉伸、压缩和弯曲状态下构件材料的许用应力计算值是根据安全系数1.33计算得出的［2］，其共同特性参数为:弹性模量2×105MPa，泊松比0.3。

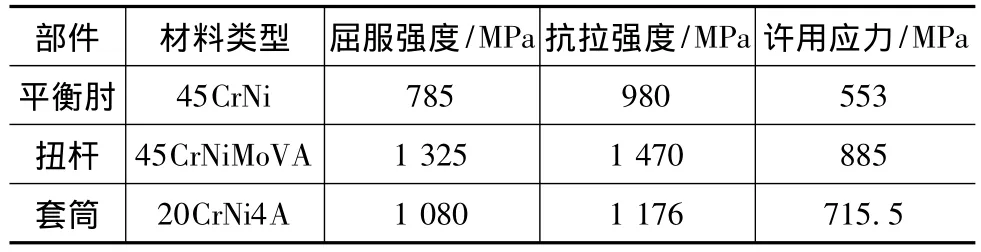
表2 部件材料和性能表

负重轮用LINK10单元模拟，在平衡肘下面距地面300mm处施加负重轮的承载力F总为

式中:n为载荷系数，取2.5;Fmax为单个负重轮在任意工况下的最大受力，Fmax=7.633kN;计算求得F总为19.082 5kN。约束加载如图4所示。

3 平衡肘有限元计算结果

在上述工况下计算得到的模型端部位移为338.876mm，沿垂直方向的端部位移为321.342mm，沿水平方向的端部位移为165.727mm。

取平衡肘到扭杆中心线距离为80mm的横截面A进行分析，图5为A截面位置和横截面示意图。图中A横截面为椭圆，长半轴a，短半轴b。

在平衡肘重力和地面支反力作用下，平衡肘暂时没有和限位器接触，没有限位器的阻力，根据下列公式计算截面A的应力［3］为

式中:Ix为A截面X轴的惯性矩;M为A截面受到的弯矩;G=154N为平衡肘自身重力;y为A截面上任意一点到X轴的距离;h为重力G到套筒中心的距离，以上几何尺寸如图5所示;σ为A截面最大的正应力。

将数值带入式(2)～式(4)计算求得A截面的最大应力为219.5MPa，采用有限元计算结果为219.648MPa，和公式计算值基本相近，说明有限元计算结果准确可信，从而可采用有限元方法进行平衡肘强度分析。

不考虑套筒上用一圈梁加强段的应力，套筒其他地方最大应力为375.028MPa，如图6所示。套筒材料许用应力为715.5MPa，安全系数为2.7，位置在套筒与平衡肘焊接连接的地方。

平衡肘上的最大应力为308.164MPa，如图7所示，在平衡肘根部与圆筒连接处，仅有微小区域。其它区域范围较小，平衡肘材料的许用应力为553MPa，满足材料的强度要求，设计是合理的。

4 扭杆有限元计算结果

采用BEAM188单元建立扭杆有限元模型，在扭杆一端建立一小段悬臂梁做为计算时施加转矩的位置，转矩大小是根据扭杆受力形式等效转化得到的。在该悬臂梁端部施加由负重轮支撑力传递的转矩M'为7.786kN·m，方向垂直扭杆横截面朝外。约束另一端端点的所有自由度，由于扭杆体积小，忽略重力产生的弯矩作用。求解计算后可得扭转角为0.702 3°，最大剪切应力为923.872MPa。

根据材料力学的理论，当同一材料制成的圆轴各段内的转矩不同或各段的直径不同(如阶梯轴)时，单位长度相对扭转角φ为

式中:Li为各段的长度;Ii为各段截面惯性矩，Ii=为各段直径;L为扭杆总长;为其剪切模量，Gx=E/［2(1+μ)］，其中钢材的弹性模量 E=200GPa，泊松比 μ =0.3。

扭杆分端部、杆部和过渡段3部分，由于过渡段长度很小，所以计算时将过渡段部分的长度与端部一起进行计算。根据式(5)计算出φ=0.643 2°，则相对误差为δ=9.19%。

相对误差不超过10%，说明对扭杆进行有限元计算是准确的。此装置中扭杆不受弯矩作用，仅有转矩作用，产生扭转剪切应力，根据强度条件［4－5］扭杆最大剪切应力为

式中:Mx为转矩;Wp为抗扭截面系数;带入数值求出τ=924.83MPa，和有限元计算值相近。许用剪切应力，可见 τ＞［τ］，故建议修改扭杆直径D，按照下式设计:

计算求得扭杆直径为42.66mm，为了满足扭转强度要求，将扭杆杆部截面直径取为43mm，端部直径取为52mm，即可保证设计要求。此设计计算值没有考虑扭杆预扭和喷丸处理时扭杆许用剪切应力的提高，一般为800～900MPa，取值须根据具体情况来确定，若最大剪切应力未超过许用剪切应力，可不按式(7)对扭杆进行重新设计。

5 平衡肘结构的拓扑优化

平衡肘是铰接式履带运输车中比较重要的零部件之一，其尺寸直接影响车体其他部件的布置。平衡肘的宽度太大，会增加车体宽度。平衡肘的长度太长，会使负重轮的布置困难;而太短又会使负重轮安装的高度降低，使履带与车厢部分发生干涉。

经以上分析，平衡肘的长宽不可做较大的改变，考虑到平衡肘的力学性能要求，在满足强度和刚度要求的基础上，本文中对该结构进行了拓扑优化，在满足最大刚度准则的条件下，使结构材料节省35%(优化时采用体积作为优化约束函数，考虑到实际的加工制造和工艺方面的要求，优化后比原体积减少35%)，提高了材料利用率，增强了结构的静态刚度。

本文中采用线性静力分析的优化设计方法，平衡肘用SOLID95三维20个节点实体单元建立拓扑有限元分析模型，该单元类型是SOLID45的高次形式，也可用于10节点四面体、13节点金字塔形五面体和15节点三棱柱五面体单元。并能应用于不规则形状而没有精确度损失，有适当的位移协调形状，适于曲线边界模拟。

计算模型及约束加载和上面静力学计算方法一致，优化时自动取材料分布为优化参数，将静力求解载荷工况下的结构柔度能量作为拓扑优化目标函数，体积作为优化约束条件，采用优化准则法(optimality criteria)，收敛精度为0.000 1，由于模型节点数多，规模大，故进行14次优化迭代计算。平衡肘节点伪密度分布图如图8所示。

从图8可看出，区域一基本不承担力，为可去掉的部分，结构的承力部分主要是区域二，由于该部分类似于悬臂梁结构，故与套筒连接的根部受力较大，平衡肘截面是变截面的，离根部越远，截面面积越小，在横截面中间可钻孔变成空心以节省材料，并可锻造加工。目标函数随迭代次数变化曲线如图9所示，目标函数迭代值见表3。

从图9可看出，随着迭代次数的变化，目标函数(结构柔度能量，用应变能来表征，单位为J)起初直线下降，在第5次迭代之后，结构柔度能量趋于稳定。优化后的体积约为6.997 3×105mm3，缩减了60%，去掉缩减部分后的单元概念模型见图10。

表3 目标函数迭代值

拓扑优化的平衡肘概念模型，只是表征受力过程中的哪些材料对承载起主要的作用，不能直接按照此模型进行设计，但通过分析该模型的材料利用特性，根据设计要求和经验，可进行结构改进。

将平衡肘的截面改成变截面等强度的结构，原来连接套筒根部是近似的椭圆型截面，自由端是空心圆截面，圆孔长度由自由端延伸通过限位块，改成根部是长半轴40mm、短半轴35mm的椭圆截面(靠车身一侧做成平面防止与车体干涉)，自由端为φ64×10mm圆形截面，孔的深度沿自由端延伸至根部60mm处。在自由端切除伸出段多余的部分，平衡肘套筒段去掉伸长部分。为了验证此结构的合理性，对新模型按照本文中的有限元计算方法进行计算，得出平衡肘根部应力最大为232.2MPa，最后形成的模型计算结果如图11所示，此模型和原来的相比体积减小了35%。