低阻力汽车外流场的数值模拟及其误差分析

熊超强，臧孟炎，范秦寅

(1.华南理工大学机械与汽车工程学院，广州 510640;2.日本大阪大学，大阪 565－087)

前言

汽车的外流场特性对其动力性、经济型、舒适性和操纵稳定性有非常重要的影响。汽车外流场的研究方法主要有风洞试验法和数值模拟法。相对于耗费巨大的模型和实车风洞试验，数字模拟在试验周期、成本和适用范围等方面有巨大的优势。但由于现阶段流体力学湍流理论和计算机性能的限制，数值模拟也须基于风洞试验结果进行研究和探索。

影响汽车外流场数值模拟精度的因素有离散误差、湍流模型误差、几何模型误差和残值误差等［1］。随着技术的发展，数值模拟的计算模型来自产品数据库，而风洞试验的模型采用数控加工，两种模型之间几何误差已经很小。计算的收敛标准一般为10－4，有的达到10－8，故残值误差也很小。因此现在外流场的数字模拟误差主要是离散误差和湍流模型误差。本文中使用SC/Tetra软件对汽车进行三维数值模拟，通过计算值和试验值在汽车升阻系数、表面压力分布和表面流线等方面的对比，探讨和分析网格(离散)和湍流模型对计算结果的影响。

1 几何模型和边界条件

本文中使用的汽车模型是日本2004－2005年度低阻力汽车创意竞赛的优秀作品，其空气动力学测试见文献［2］。模型尺寸如图1所示。

为了保证一致性，三维数值模拟和风洞试验都采用1/5模型，计算区域包括风洞和车身。计算模型入口条件为质量流量54.27kg/s，以保证风洞试验段空气平均流速为30m/s。出口条件为参考压力p=0。风洞、地面和车身均为固定壁面。计算区域如图2所示。沿车身表面共设65个压力测试点，图3示出其中10个测点。

2 网格对外流场计算的影响

计算区域内的网格尺寸和网格结构都会对计算结果造成影响。本文中各计算模型均采用以四面体为主的非结构网格划分流体区间，沿壁面插入棱柱边界层单元后，形成的四面体、六面体和棱柱的混合网格如图4所示。

2.1 边界层网格

湍流模型是针对充分发展的湍流流动建立的，因此不适用于近壁面低雷诺数流动的计算。近壁面处理常用两种方法，一种是壁面函数法，另一种是直接数值求解法。不同的近壁面处理方法对y+值有不同的要求。y+是指壁面第一层网格离壁面的无因次距离，其表达式为

式中:ρ为密度;y为壁面的距离;μ为分子黏性系数;u*为壁面摩擦速度。计算中一般通过控制底层网格厚度Ym来控制y从而达到控制y+值的目的。现普遍认为y+＜11.6时网格节点位于黏性层内;y+＞30时网格节点位于对数律层内;11.6＜y+＜30时网格节点位于从黏性层向对数律层的过渡区域内。y+值会影响近壁面处理的精确性，从而影响到整个三维数字模拟的结果。

2.1.1 y+对k-ε湍流模型计算精度的影响

对于k-ε系列湍流模型，若近壁面采用直接数值求解，通常要求y+＜1，外流场模拟中会因网格数目巨大而无法实现，同时为了减小其黏性层内精度较低带来的影响，k-ε模型的近壁面处理通常采用对数律壁面函数法。

矿区采用工业矿体品位为≥8%；3.5%≤低品位工业矿体品位<8%的标准，在区内圈定了3条矿化带、1条晶质石墨工业矿体、13条晶质石墨低品位矿体(表1)。

对数律壁面函数法的基本思想是在湍流核心区域采用湍流模型计算，在壁面黏性区域不求解，通过壁面上的物理量和半经验公式直接得到底层体网格节点变量值［3］。在划分网格时须将第一层网格内节点布置在对数律成立的区域内，否则会导致计算偏离实际。所以对于k-ε系列湍流模型，要求30＜y+＜100，最好靠近30一端。

表1中a、b两模型湍流区域网格相同，仅车身表面边界层网格厚度和层数不同，其中a边界层网格厚度较小，y+位于7～13的范围内，b网格大部分y+位于30周围。从两网格Standard k-ε模型计算所得阻力系数(升力系数严重偏离试验值，不作为比较项)可知，对于k-ε湍流模型，Ym的厚度保证在y+=30周围即可，继续细化底层网格反而会降低计算精度。

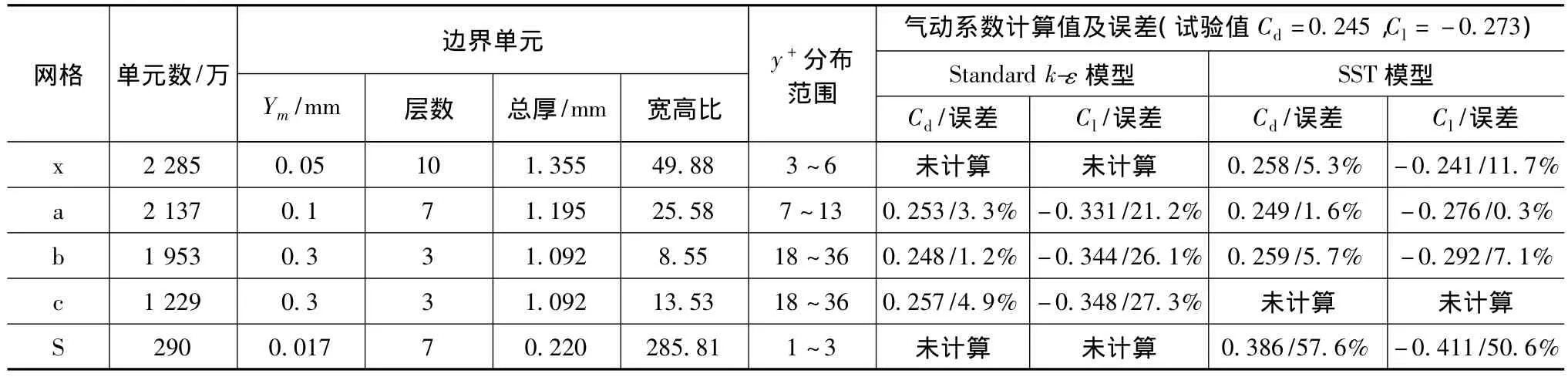
表1 网格和湍流模型对计算的影响

2.1.2 y+对SST k-ω湍流模型计算精度的影响

SC/Tetra中SST k-ω模型会根据y+值来确定第一层网格的处理方法。当y+＜1时采用直接数值求解;当1＜y+＜11.6时，SST模型默认采用低雷诺自适应壁面函数(LRN adaptive wall function，LRN AWF)［4］;当11.6＜y+＜1 000 时和 k-ε 模型相同，采用对数律壁面函数法。

表1中a、b和x网格模型湍流区域的网格相同，车身表面边界层网格厚度和宽高比不同。从表1中三网格采用SST模型的计算结果可知:a网格7＜y+＜13，采用LRN AWF法，且宽高比小于30，能够获得较高的计算精度;x网格虽然也采用LRN AWF法，但因网格3＜y+＜6，位于该函数精度最低的y+=4.7周围的混合区域，且宽高比大于30，故计算精度低于网格a;b网格y+＞11.6，采用和k-ε相同的对数律壁面函数法，计算精度较a低。

理论上，当网格达到y+＜1，且边界层网格宽高比小于10时，能获得最精确的解。但在汽车外流场计算中，上述要求使网格数目过亿，故还无人验证。

除y+值外，网格的边界层总厚度也会影响计算精度。SST k-ω湍流模型边界层内从第二层网格开始采用k-ω计算并平滑过渡到k-ε模型，若网格边界层总厚度远小于实际边界层厚度，边界层的计算和过渡会在四面体网格上完成，从而降低计算精度。如表1中s网格虽然1＜y+＜3，但其边界层总厚度过小且宽高比太大，故计算结果和试验相差极大。

2.2 湍流区域网格

不同网格车身表面压力系数分布情况的对比见图5，由图可知，网格尺寸对压力系数分布的影响主要体现在车身尾部。粗细网格在上表面中线上压力系数基本一致，而在尾部中线上，细网格(b网格)的压力系数大小和分布趋势更接近于试验结果。

综上所述，在其它计算条件相同的情况下，边界层网格厚度须根据湍流模型而控制在相应的范围内。边界层外网格越密，截断误差越小，计算精度越高，但网格数量受计算机性能的限制，故多采用局部网格加密的方法。

构建以四面体为主的流体非结构网格时除要求在物理量梯度大的地方网格单元足够小、疏密网格变化平缓均匀、网格单元不出现严重扭曲外，边界层网格的正交性和底层网格厚度起着决定性影响。

3 湍流模型对外流场计算的影响

湍流模型由于引入经验和半经验公式及经验常数，使其描述的流动和真实流动之间存在差别。计算时要选择最能反映流动情况的湍流模型以减小计算误差。下面将以表1中数据为基础，分析比较目前应用广泛的Standard k-ε湍流模型和在外流场计算中应用日益增多的SST k-ω湍流模型。

3.1 湍流模型介绍

Standard k-ε湍流模型的优点是对网格要求较低，求解稳定且易收敛，但其湍流尺度未知，仅局限于湍流边界层压力相对稳定的情况，且壁面函数在边界层的修正中难以弥补计算模型与实际物理现象之间的差距。

基本k-ω湍流模型的特点是能够精确模拟边界层的物理现象，但对来流条件非常敏感，入口边界处ω微小变化都可能使模拟结果变化很大［5］。

SST k-ω湍流模型采用k-ω模型求解近壁面区域，采用k-ε模型求解湍流区域，且两模型之间能够平滑过渡，使SST k-ω湍流模型有很好的精确性和鲁棒性［6］。SST k-ω湍流模型最初用于航空航天领域，因其在近壁面区域的优势，在汽车流场计算中的应用日益增多。

3.2 气动参数计算结果的比较

从表1中a、b网格计算数据可以看出，SST模型计算得到的气动参数更精确。虽然Standard k-ε模型的阻力系数结果非常接近试验值，但升阻系数严重偏离试验值，说明其未能准确地模拟流场情况。

计算过程中发现，车身底部流域由于受到地面、车轮和车身底面形状的影响，空间狭小且形状复杂，网格质量难保证，使气动升力计算结果难收敛，是外流场计算中的难点。

3.3 表面压力系数分布的比较

图6为不同湍流模型压力系数分布结果的比较。由图可见:湍流模型对上表面压力系数大小和分布趋势的影响较小;尾部中线上SST的压力系数比Standard k-ε更接近试验值。

3.4 表面流线的比较

图7为表面流线的比较。由图可见:由于车身表面光滑，过渡平缓，两湍流模型模拟的车身上表面流线差别较小;两湍流模型都捕捉到了汽车模型的两个尾涡，但Standard k-ε模拟的两个尾涡大小不一致，SST k-ω模型模拟的尾涡的对称性更好。

4 结论

(1)从近壁面处理方法的原理出发，提出了使用k-ε和SSTk-ω湍流模型时，y+应控制的具体范围。在保证y+的同时，边界层网格的总厚度和宽高比也应控制在一定范围内以保证计算精度。

(2)从升阻系数、压力系数分布和表面流线3个方面说明了SST k-ω模型结合低雷诺数自适应壁面函数的计算结果更接近试验值。

(3)通过实例证明了如果能保证网格的合理性，采用四面体为主的非结构网格也能达到小数点后三位的计算精度。

［1］严鹏，吴光强，傅立敏，等.轿车外流场数值模拟［J］.同济大学学报，2003，31(9):1082 －1086.

［2］日本自動車技術会CFD技術部門委員会.CFDベンチマーク用風洞実験モデルデータの公開、技術報告書［EB/OL］.http://www.bookpark.ne.jp/cm/jsae/cat107.asp，2008.

［3］王福军.计算流体动力学分析［M］.北京:清华大学出版社，2004:113－131.

［4］SC/Tetra V7 User's Guide［G］.Software CRADLE Inc.

［5］吴军，谷正气，钟志华.SST湍流模型在汽车绕流仿真中的应用［J］.汽车工程，2003，25(4):326 －329.

［6］Menter F R，Kuntz M，Langtry R.Ten Years of Industrial Experience with the SST Turbulence Model［J］.Turbulence，Heat and Mass Transfer，2003(4):1 －3.