基于模糊覆盖的粗糙模糊集模型
2012-07-16韩浩瀚谢祥云
韩浩瀚,谢祥云
基于模糊覆盖的粗糙模糊集模型
韩浩瀚,谢祥云
(五邑大学 数学与计算科学学院,广东 江门 529020)
构造了基于模糊覆盖的粗糙模糊集模型,从理论上论证了定义的合理性,刻画了模糊覆盖粗糙集的一些基本性质.
模糊集;模糊覆盖;模糊覆盖近似空间;粗糙模糊集
粗糙集理论通过等价关系对论域进行划分,并用论域上的一对上下近似算子作用于集合(概念)来刻画对象,从而发现信息系统中一些隐藏的知识[1]. 粗糙集理论和模糊集理论在处理不确定性和不精确性问题方面推广了经典集合论,两种理论的比较和融合一直是热点话题,其中模糊粗糙集理论模型[2-4]的建立和发展,已成为粗糙集理论推广的主要方向之一. 经典粗糙集理论的另一个拓展方向是弱化等价关系:Zakowski从实际出发,提出了覆盖粗糙集模型[5],并研究了相关的性质;William Zhu等[6]在覆盖粗糙集的理论基础上给出了知识约简和算法;胡军等[7]将覆盖粗糙集模型扩展到覆盖粗糙模糊集模型. 本文在文献[7]的基础上,将覆盖拓展为模糊覆盖,为此我们做了以下工作:1)构造了模糊覆盖粗糙集的定义,并阐述其合理性;2)阐述并证明了基于模糊覆盖的粗糙模糊集的一些基本性质.
1 预备知识
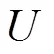
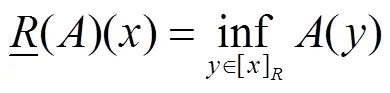
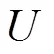
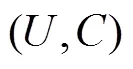
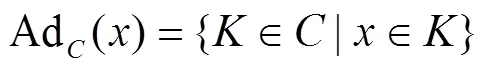
文献[7]给出了一个模糊集在一个覆盖近似空间中的上下近似的概念及性质,见定义4.
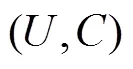
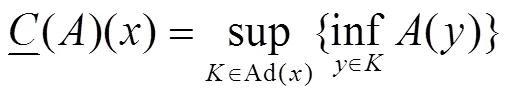
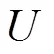
2 基于模糊覆盖的粗糙模糊集模型
模糊集与粗糙集都是为了处理模糊不清、不确定的概念而对经典集合论推广的结果,将二者结合起来进行研究通常是理论拓展的方法之一;另外,信息表中连续值属性的存在也是我们研究模糊关系和模糊覆盖下的粗糙集理论的重要原因之一. 下面给出基于模糊覆盖的粗糙模糊集的定义.

下面研究定义6和定义4的关系.
定理1 基于模糊覆盖的粗糙模糊集是基于覆盖的粗糙模糊集的推广.
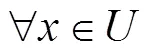
定理2 基于覆盖的粗糙模糊集是粗糙模糊集的推广.
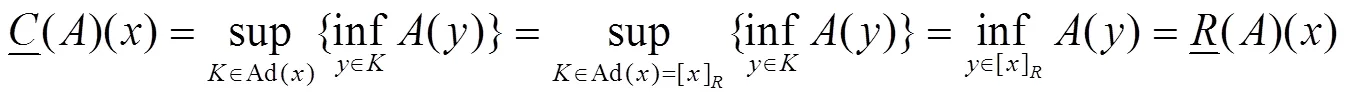
由于粗糙模糊集与基于覆盖的粗糙模糊集均具有对偶性,故可以得到上近似也成立. 所以基于覆盖的粗糙模糊集是粗糙模糊集的推广.
定理3[3]226粗糙模糊集是Pawlak粗糙集的推广.
由此可见,本文对基于覆盖的粗糙模糊集所做的推广工作与前人的工作一脉相承,与整个粗糙集理论体系具有高度的融合性.
3 基于模糊覆盖的粗糙模糊集的性质
在所有关于粗糙集推广模型的研究中,粗糙集上下近似的对偶性与幂等性一直是备受关注的重要性质. 上下近似的对偶性使得上下近似之间可以相互转换,从而赋予粗糙集理论对称美和简单美,并使得被近似集合与其补集具有相同的边界,达到理论与现实世界的高度吻合. 幂等性的满足是定义对自身合理性的证明,同时说明在此定义下,一次运算即达最佳逼近,该运算具有高效性与确定性.
4 结束语
本文继承前人的工作,构造了基于模糊覆盖的粗糙模糊集模型,该模型可以包含以往所有的粗糙集模型,且保持了经典粗糙集理论的优良性质,如对偶性、幂等性等,可以视之为优良的理论拓展. 后继工作将在模型的应用实例、公理化、实际含义等方向上展开. 另外模型与粒度计算的融合方面仍需更进一步的研究和探索.
[1] KRYSZKIEWICZ M. Rough set approach to incomplete information system[J]. Information Sciences, 1998, 112: 39-49.
[2] GRECO S, MATARAZZO B, SLOWINSKI R. Fuzzy similarity relation as a basis for rough approximations[C]// RSCTC’98 Proceedings. Heidelberg: Springer-Verlag, 1998: 283-289.
[3]DUBOIS D, PRADE H. Rough fuzzy sets and fuzzy rough sets[J]. International Journal of General Systems, 1990, 17: 191-209.
[4]黄正华,胡宝清. 模糊粗糙集理论研究进展[J]. 模糊系统与数学,2005(4): 125-134.
[5] ZAKOWSKI W. Approximation in the space (U, ∏)[J]. Demonstratio Mathematica, 1983, 16(3): 761-769.
[6]ZHU W, WANG Feiyue. Reduction and axiomization of covering generalized rough sets[J]. Information Sciences, 2003, 152: 217-230.
[7]胡军,王国胤,张清华. 一种覆盖模糊集模型[J]. 软件学报,2010, 21(5): 968-977.
[8]BONIKOVSKI Z, BRYNIARSKI E, WYBRANIEC U. Extensions and intentions in the rough set theory[J]. Information Sciences, 1998, 107: 149-167.
A Fuzzy Rough Set Model Based on Fuzzy Covering
HANHao-han, XIEXiang-yun
(School of Mathematics and Computation Science, Wuyi University, Jiangmen 529020, China)
A rough fuzzy set model based on fuzzy covering is constructed, the rationality of its definition is demonstrated in theory and some basic properties of the model are portrayed.
fuzzy sets; fuzzy covering; fuzzy covering approximation space; fuzzy rough sets
1006-7302(2012)02-0001-04
O159
A
2012-01-06
国家自然科学基金资助项目(10961014);广东省科技计划资助项目(2010B010600039);广东省自然科学基金资助项目(S201101000368)
韩浩瀚(1985—),男,河南南阳人,在读硕士生,研究方向为粗糙代数与智能计算;谢祥云,教授,博士,硕士生导师,通信作者,研究方向为序半群的代数理论、模糊代数、粗糙集理论.
