基于广义反调和均值的弱化缓冲算子的构造及其应用

段琪斌，陈勇明

(成都信息工程学院 数学学院,成都 610225)

0 引言

1984年,邓聚龙教授首次提出了灰色动态模型GM(n,h)[1],此后该模型在工程技术、农业生产、经济管理等众多领域获得了广泛应用。刘思峰教授[2-4]研究发现对于冲击扰动系统直接应用经典GM(1,1)模型并不理想，提出了缓冲算子的概念和构造缓冲算子所依据的缓冲算子3条公理，并利用缓冲算子的工具来解决冲击扰动系统的定量预测与定性分析结果不吻合的问题，在实践中取得了比较满意的效果。缓冲算子分为弱化缓冲算子和强化缓冲算子，分别应用于两种不同类型的存在冲击扰动的原始序列。对于原始数据序列的前半部分增长(衰减)速度较快,后半部分增长(衰减)速度较慢时,利用弱化缓冲算子首先对原始数据序列进行作用,然后再进行建模[5]；对于原始数据序列的前半部分增长(衰减)速度较慢,而后半部分增长(衰减)速度较快时,在进行预测时首先应对原始数据序列进行强化缓冲算子作用,然后再进行建模[6]。弱化缓冲算子和强化算子能有效地消除冲击扰动系统数据序列在建模预测过程的干扰，于是研究如何构造强化缓冲算子和弱化缓冲算子成为提高GM(1,1)模型建模精度的一个重要方向,人们从不同角度出发构造出了一系列缓冲算子[5-6]。本文将从另外一个角度利用广义调和均值构造一类新的弱化缓冲算子，从而使序列前一部分增长(减缓)速度过快,后一部分增长(衰减)速度过慢的冲击扰动系统数据序列,在建模预测过程中出现的定量预测结果与定性分析结论不符的问题得到有效解决，并且比已有的一些弱化缓冲算子在应用中具有更好的效果，使建模精度得到更大程度提高。

1 预备知识

作为后面工作的预备知识，我们先给出有关缓冲算子的一些基本概念、构造缓冲算子的3条公理以及判断弱化缓冲算子的相关定理。

定义1(单调增长序列、单调减少序列、振荡序列)[7]设X=(x(1),x(2),…,x(n))为系统行为数据序列.若∀k∈｛2，3，…,n｝,x(k)-x(k-1)＞0，则称X为单调增长序列；若 ∀k∈｛2，3，…,n｝,x(k)-x(k-1)＜0，则称X为单调衰减序列；若∃k,k′∈｛2，3，…,n｝，有x(k)-x(k-1)＞0,x(k')-x(k'-1)＜0,则称X为振荡序列，又设则称M-m为振荡序列X的振幅。

定义2 (缓冲算子)[7]设X为系统行为数据序列,D为作用于X的算子,X经过算子D作用后所得序列记为XD=(x(1)d,x(2)d,…,x(n)d),其中x(i)d(i=1,2,...,n)为算子D作用于x(i)的结果，满足以下3个条件的算子D称为缓冲算子：(1)x(n)d=x(n)(不动点公理)；(2)系统行为数据序列X中的每一个数据x(k),k∈{1,2,…,n}都应充分参与算子作用的全过程(信息充分利用公理)；(3)任意的x(k)d,k∈{1,2,…,n}均可由一个统一的x(1),x(2),…,x(n)的初等解析式表达(解析化公理)。上述(1)(2)(3)称为缓冲算子三公理。

定义3(弱化缓冲算子)[7]设X为系统行为数据序列,D为缓冲算子.当X分别为增长序列、衰减序列或振荡序列时，若缓冲序列XD比原始序列X的增长速度(或衰减速度)减缓或振幅减小,则称缓冲算子D为弱化缓冲算子，简称弱化算子。

对于弱化缓冲算子有如下判别性质：

定理1[7]设X=(x(1),x(2),…,x(n))为系统行为数据序列,x(i)＞0,i∈{1,2,…,n},其缓冲序列为XD=(x(1)d

,x(2)d,…,x(n)d)。(1)当X为单调增长序列,则D为弱化算子 ⇔x(k)≤x(k)d，k∈{1,2,…,n}；(2)当X为单调衰 减 序 列,则D为 弱 化 算 子 ⇔x(k)≥x(k)d，k∈{1,2,…,n}；(3)当X为振荡序列,D为弱化算子⇔

2 新缓冲算子的构造

下面基于广义反调和均值[8]，我们构造一类新的弱化缓冲算子。

定理2 设X=(x(1),x(2),…,x(n))，x(i)＞0，i∈{1,2,…,n}为系统的原始行为数据序列，对于k∈{1,2,…,n},令XDGAHAM=(x(1)dGAHAM,x(2)dGAHAM,…,x(n)dGAHAM)，其中：

则有:

当a＞1时，DGAHAM对于单调增长序列和单调衰减序列都是弱化算子；

当a≤0时，无论X是单调增长序列还是单调衰减序列，或是震荡序列，DGAHAM都是弱化算子。

我们将上述缓冲算子称为广义反调和均值弱化缓冲算子，简记为GAHAM弱化算子(Generalized Anti-HArmonic Mean)。

下面给出定理的证明。

证明：首先验证构造的GAHAM算子满足缓冲算子的3条公理。=x(n)即满足不动点公理。

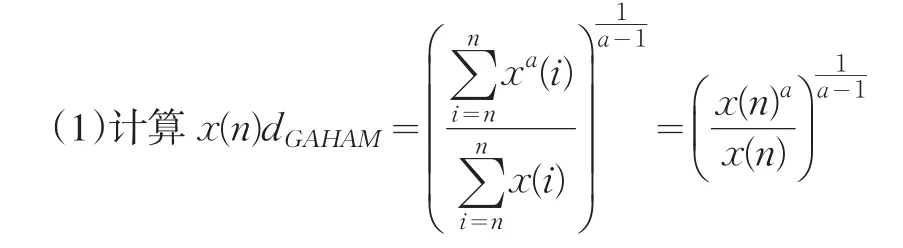
（2）从GAHAM算子表达式可知系统行为数据序列X中的每一个数据x(k)，k∈{1,2,…,n}都充分参与算子作用的全过程，即满足信息充分利用公理。

（3）任意的x(k)，k∈{1,2,…,n}

为x(1),x(2),…，x(n)的初等解析式表达，即满足解析化规范化公理。

由以上（1）（2）（3）可知GAHAM算子满足缓冲算子的三条公理。

其次证明GAHAM算子是弱化算子。依据弱化算子的判别定理1证明。

计算：

(1)当a＞1时：

①若x(k)为增长序列，对于i＞k有x(i)＞x(k)，则

由（1）式所以有x(k)dGAHAM≥x(k)，由定理 1知DGAHAM是弱化算子；

②若x(k)为衰减序列，对于i＞k有x(i)＜x(k)，则

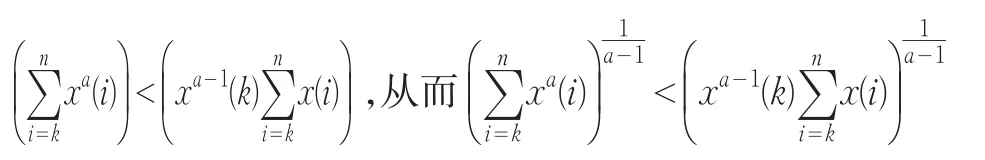
由（1）式所以有x(k)dGAHAM≤x(k)，由定理1知DGAHAM是弱化算子。

（2）当a≤0时：

①若x(k)为增长序列，对于i＞k有x(i)＞x(k)，则

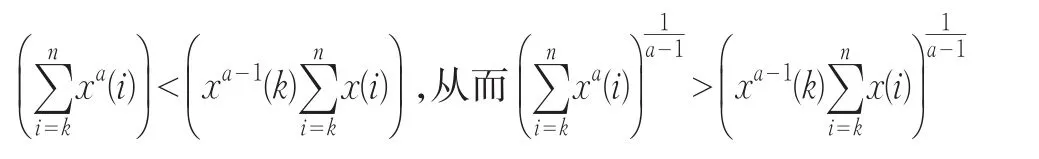
由（1）式所以有x(k)dGAHAM≥x(k)，由定理1知DGAHAM是弱化算子；

②若x(k)为衰减，对于i＞k有x(i)＜x(k)，则

由（1）式所以有x(k)dGAHAM≥x(k)，由定理1知DGAHAM是弱化算子；

③当x(k)为随机振荡序列，记≥m，由定理1知DGAHAM是弱化算子。

注1：当a=0时，此时GAHAM算子为平均弱化缓冲算子[18](AWBO)，即平均弱化缓冲算子为GAHAM弱化缓冲算子的一个特例，GAHAM弱化缓冲算子推广了现有结果，更具一般性。

注2：序列算子的作用可以多次进行，若D1、D2皆为序列算子,则D1D2为二阶算子，XD1D2=(x(1)d1d2,x(2)d1d2,…,x(n)d1d2)，类似的有三阶、四阶算子等等[17]。对于GAHAM算子，

①当a＞1时，对于单调增长序列和单调衰减序列，二阶GAHAM算子都是弱化算子；

②当a≤0时，对于单调增长序列、单调衰减序列和振荡序列，二阶GAHAM算子都是弱化算子。

证明与定理2类似，从略。

3 算例分析

为了说明本文构造的GAHAM缓冲算子对有扰动的序列建立GM(11)模型中的实用性，利用文献[20]中的数据建立GM(11)模型，并从建模精度上将GAHAM缓冲算子和已有的一些弱化缓冲算子作比较。

代表某市1997～2005年工业总产值的系统行为数据序列[9]X=(187.85,303.79,394.13,498.27,580.43,640.21,702.34,708.86,716.95)，该序列前期增长快而后期增长慢，该市工业发展前期国家给予了特殊的产业政策，在发展比较成熟的后期特殊政策取消，这是一个比较典型的存在扰动的工业产值系统，适合用弱化缓冲算子处理后再建立GM(11)模型。

对上述数据,文[20]中的弱化缓冲算子

对数据进行弱化处理建模后的相对误差和一步预测误差见表1。

下面以本文构造的GAHAM缓冲算子建立模型。

对GAHAM缓冲算子中的参数a，采用计算机模拟选择a=15.5，原序列X经一阶GAHAM缓冲算子处理得

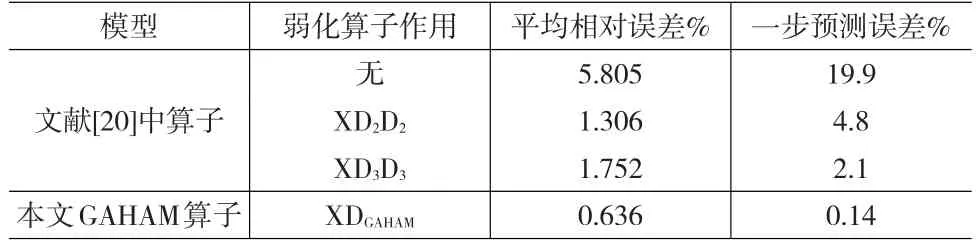
表1 不同弱化算子建模效果比较

建立GM(1,1)模型为：

该模型的平均相对误差为0.636%低于千分之一，一步预测误差为0.141%低于千分之一，结果列于表1最后一行。2004年和2005年的预测值分别为707.3536和719.4147亿元，这样实际情况相符。

从表1可以看出，本文的GAHAM缓冲算子的平均相对误差和一步预测误差均低于前2种缓冲算子，从而优于已有的2种弱化缓冲算子，另外，已有的2种缓冲算子作了二阶处理，本文的GAHAM缓冲算子只作了一阶缓冲处理。

4 结束语

本文构造的GAHAM弱化缓冲算子，适用于存在冲击扰动的前半部分增长(衰减)速度较快而后半部分增长(衰减)速度较慢的系统行为序列。从理论上，GAHAM弱化缓冲算子以平均弱化缓冲算子为特例，推广了前人的研究结果。从实践上，通过本文的GAHAM弱化缓冲算子处理再建立GM(1,1)模型比已有的一些缓冲算子有更好的实践效果，说明具有一定的实际应用价值。

[1] 邓聚龙.灰色动态模型(GM)及在粮食长期预测中的应用[J].大自然探索,1984,(3).

[2] 刘思峰,赵理.弱化算子与长葛县乡镇企业发展预测[J].河南农业大学学报,1990,(3).

[3] Liu Sifeng.The Three Axioms of Buffer Operator and their Application[J].The Journal of Grey System,1991,3(1).

[4] 刘思峰.冲击扰动系统预测陷阱与缓冲算子[J].华中理工大学学报,1997,25(1).

[5] 党耀国,刘思峰等.关于弱化缓冲算子的研究[J].中国管理科学,2004,12(2).

[6] 党耀国,刘斌,关叶青.关于强化缓冲算子的研究[J].控制与决策,2005,20(12).

[7] 刘思峰,党耀国等.灰色系统理论及其应用(第五版)[M].北京：科学出版社,2010.

[8] 匡继昌.常用不等式(第三版)[M].济南:山东科学技术出版社,2004.

[9] 崔杰,党耀国.一类新的弱化缓冲算子的构造及其应用[J].控制与决策,2008,23(7):741-744.