正态分布的哲学本质及其社会经济应用意义

2012-07-12郑文兵

统计与决策 2012年7期

郑文兵

（湛江师范学院法政学院，广东湛江 524048）

0 引言

正态分布，又名高斯分布，是概率论中最重要的一种分布，一种最常见的连续性随机变量的概率分布，也是自然界最常见的一种分布。在数学、物理及工程等领域都非常重要，在统计学的许多方面有着重大的影响力。正态分布的概念是由德国的数学家和天文学家Moivre于1733年首次提出的，但由于德国数学家Gauss率先将其应用于天文学家研究并对后世的影响极大，所以使正态分布同时就有了“高斯分布”的名称[1]。该分布由两个参数——平均值μ和方差σ2决定。概率密度函数曲线以均值为对称中线，方差越小，分布越集中在均值附近。

如果一个随机变量X的概念密度函数为：则表明该随机变量X服从一个数学期望为μ、方差为σ2的正态（高斯）分布，其期望值μ决定了分布的位置、其标准差σ决定了分布的幅度。因其曲线呈钟形状态，因此人们又经常称之为钟形曲线。我们通常所说的标准正态分布是μ=0，σ=1的正态分布。

1 自然界中广泛存在着正态分布

正态分布理论具有广泛的应用。大量实践经验和理论分析表明，许多自然现象和社会现象都可以看作服从或近似服从正态分布[2]。生产与科学实验中很多随机变量的概率分布都可以近似地用正态分布来描述。例如，在生产条件不变的情况下，产品的强力、抗压强度、口径、长度等物理指标；同一种生物体的身长、体重等指标；同一种种子的重量；测量同一物体的误差；弹着点沿某一方向的偏差；某个地区的年降水量；理想气体分子的速度分量；医学现象诸如同质群体中的红细胞数、血红蛋白量；一个人口群体的智商；一组人的某科目考试成绩；实验中的随机误差，等等，均呈现为正态或近似正态分布。有些指标（变量）虽服从偏态分布，但经数据转换后的新变量可服从正态或近似正态分布。其中，经对数转换后服从正态分布的指标，被称为服从对数正态分布。同时，正态分布曲线还描述了许多心理检验得分；这个曲线还成为了不同种族的智力测验的得分分布的争论焦点[1]。

一般来说，如果一个现象是由许多微小的独立随机因素共同影响的结果，那么就可以认为这个现象具有正态分布。从理论上看，正态分布具有很多良好的性质，许多概率分布可以用它来近似；还有一些常用的概率分布是由它直接导出的，例如对数正态分布、t分布、F分布等[3]。

2 正态分布所体现的哲学意义

2.1 正态分布从数学上证明了世界事物分布不（非）均匀的特征

在联系自然、社会和人类思维的实践背景下，我们以正态分布的本质为基础，以正态分布曲线及其面积分布图为表征，进行抽象与提升，可以抓住正态分布论的主要内涵归纳为正态哲学。这种哲学的主旨就是世界是不（非）均匀，也就是事物是不平均、不等分地分布着的，世界上的任何事物和结构都普遍存在着中心和外围两类状态，并与辩证唯物主义哲学的重点论理论相印证着。正态分布曲线及面积分布图非常清晰的展示了事物的重心，那就是占事物整体68.27%的基区，是主体、是重点、是中心，所以要重点抓。一倍标准差以外到正、负无穷远的面积才占了31.73%，这恰好又展示了事物的外围。

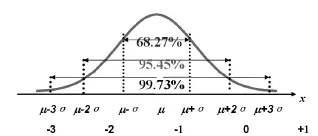
图1 常用的正态概率值（在一般正态分布及标准正态分布中比较）

这就从数学上证明了世界是普遍的存在着中心和外围的特征的，世界上的事物是不均匀的。人类在认识世界和改造世界的过程中一定要抓住重点、中心，因为重点、中心就是事物的主要矛盾，它对事物的发展起主要的、支配性的作用。抓住了重点、中心才能一举其纲，万目皆张。事物和现象纷繁复杂，在千头万绪中不抓住主要矛盾，就会陷入无限琐碎之中。由于我们时间和精力的相对有限性，出于效率的追求，我们更应该抓住重点、中心。正态分布中基区所表现出的主体和重心意义，也正好和人类生活中的经验智慧，比如“马太效应”和20/80的“二八法则”不约而同的吻合着。

2.2 正态分布从数学上证明了概率分布的不（非）均匀性

统计学上有古典概率、统计概率和主观概率三种概率分类。古典概率的定义就是某种事件A所包含的基本事件个数M与其样本空间中基本事件总数N的比值。古典概型（又叫等可能概型）认为有等概率的事件和现象发生，比如抛掷一枚均匀硬币的现象，当硬币落下来的时候，正面朝上和反面朝上的概率是一样的；还比如投掷一颗均匀骰子的时候，当骰子落定以后，骰子的6个面中每一面朝上的概率也是一样的[4]。可是这种事件和现象概率相等的条件必须具有以下两种基本特点：

其一，事件的每次试验的可能结果有限，即样本空间中基本事件的总数是有限的；

其二，每个试验结果即每个基本事件（样本点）出现的可能性相同。

于是，从这里我们就可以清晰地看到，这种概型就是已经假设了事物是均匀分布的，也就是先事先假定事件是等概率的，然后再用它判断事件是等概率的，用主观代替客观。所以，这种概率理论其实就是首先做出了一个事物出现、分布是相等概率的假设，然后又根本不加以检验或者无法加以检验后就直接地判定这个假定是成立的、不能被拒绝的，也就是用假设来证明假设是成立的，在理论上陷入了错误和混乱，在逻辑上也是前后循环和自相矛盾。事实上，笔者认为这是一种典型的人为假想的、孤立的、静止的、唯心的概率观。一旦联系到客观世界以后，并用普通联系和永恒发展的辩证观点来考察事物的概率以后，我们马上就可以发现这种概率理论是需要修正的。比如，对于一个怀孕的女性，我们说她将来生育女孩和生育男孩的概率是相等的，都是0.5的概率。可是，一个人口群体中，男孩和女孩的出生性别比一般是103～105:100，或者为103～107:100[5]，这里就不再是0.5的概率了。再比如说，两点分布即贝努利实验中，实验结果只有两种可能，可是每一种结果出现的概率P却不一定相等了，因为此时我们没有确定事物是均匀分布的。某种结果即事件A出现的概率为P(A)=p，而另一种结果即事件A的对立事件Aˉ出现的概率则为P(Aˉ)=(1-p)，很显然p不一定等于(1-p)了。再比如，在N重贝努利实验中的某种结果B出现的次数X的概率分布就为P(X=k)=Cknpk(1-p)n-k，也很清晰，这里每一种结果出现的概率也是不相等的。同理，超几何分布、泊松分布等概率类型的分布中也是这种结果。

而统计概率则是历史上同类事物发生的稳定的频率，其数学表达式为：

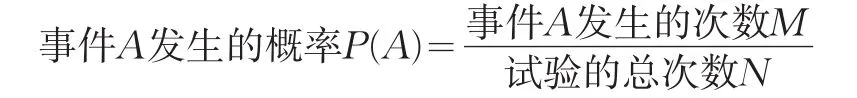
很显然，这是一种不以人们的意志为转移的客观概率，毫无人类主观的成分在内。同时，我们也可以很清晰地看出，统计概率的分布是不均匀的。

主观概率则是合理的信念的测度，是某人对特定事件会发生的可能的度量，即他相信（认为）事件将会发生的可能性大小的程度。这种相信的程度是一种信念，是主观的，但又是根据经验、各方面的知识，对客观情况的了解进行分析、推理、综合判断而设定的，与主观臆测不同。主观概率不认为事物的概率分布是均匀的。

总之，结合各门学科和各方面的情况后，我们认为世界上概率的分布是不均匀的。

这种概率不均匀、不平均的特性可以在正态分布中得到清晰的说明。正态分布的概率密度曲线的坐标系通常是这样确定的：横轴为变量轴，表示事物数量方面取值的变化；而纵轴是概率轴，表示事物数量某种取值概率的大小。从正态分布函数的概率密度曲线来看，很明显地可以看出事物取不同变量值的概率是不一样的，靠近中心的地方取值概率大，往两边延伸的地方取值概率小，离开均值越远的地方取值的概率越小。

所以，正态分布的概率密度曲线告诉我们，我们所处的这个世界上不但存在着各种事实上的不均匀、不平均，而且还是概率上的不均匀、不平均，也即机会上的不平均，或者说各种事实上的不平均本身就是概率不平均、不均匀的具体表现和客观化。所以，笔者认为追求事实平均和机会平均都是不可能的，这直接与自然法则相背道而驰。这就是正态分布的哲学本质和世界观意义。

3 正态分布能够广泛地适用于人类社会现象、经济现象的研究

客观世界作用于事物各个个体的因素分为基本因素和次要因素两类，基本因素决定事物的必然规律，次要因素使事物呈现统计规律。人们所能认识而且能够控制的因素是基本因素，而大量的次要因素未能为人们所认识或未能被人们所控制，但只要存在次要因素的影响，就必然会有所表现。人类社会的社会生活和经济生活中，也大量的存在着各种影响人们社会生活和经济生活的主要因素和次要因素。迄今为止，暂时还没有相关的文献表明社会、经济现象不是随机现象。

大量的文献认为社会、经济现象是随机现象的，许多学者进行了类似的尝试。例如，黄良文就认为一些社会和经济现象是随机事件，像农作物的每亩产量、人口的出生数和死亡数、生产的废品数和合格品数、市场交易额、经营中的盈与亏等等现象，都是典型的经济随机事件[6]。同时，他还认为水产养殖中鱼的体重、棉花纤维长度、机械零件尺寸、厕量误差等等，都服从正态分布[7]。

袁卫、庞浩、曾五一等也认为一些社会和经济现象属于随机事件，例如他们认为消费者对于饮料的不同偏好、某座写字楼每平方米的出租价格、产品质量中的合格率和次品率、某餐厅的日营业额、某电话用户每一次通话时间长度等等，都是随机现象。[4]

贾俊平、何晓群、金勇进等也认为，在社会和经济现象中有许多随机变量的概率分布都服从正态分布，如同龄组儿童的发育特征，如身高、体重、肺活量；某一公司的年销售量；同一条件下产品的质量分布等等[8]。

王长江、郝华荣等也认为许多的自然现象和社会、经济现象中，大量的随机变量都服从或者近似服从正态分布[3]。

Gudmund R.Iversen and Mary Gergen等认为国民的政治倾向和投票行为、人们的慈善行为、人们的旅游行为、人们的汽车消费等都是随机事件的，都服从或近似服从正态分布[1]。

朱建平、孙小素等认为保险公司的盈亏服从或者近似服从正态分布[2]。

张德存等认为农作物的产量、人们出行路线的选择、产品的规范等现象服从或者近似服从正态分布[9]。

一种商品的需求数量是由许多因素共同决定的。其中，主要的因素有：该商品的价格、消费者的收入水平、相关商品的价格、消费者的偏好以及消费者对该商品的价格预期等等。

同样的，一种商品的供给数量也取决于多种因素的影响。商品价格的高低、生产成本的大小、生产的技术水平、相关商品的价格、生产者对未来的预期等因素都会对商品的价格产生随机影响。

商品的价格不仅由需求和供给决定，还有其它的很多因素也在随机的影响着。例如，成本、消费者的偏好、边际效用、相关商品的价格、最高限价和最低限价、财政和货币政策、信贷投资、消费者的风险态度等等因素都共同影响商品的价格。

消费者的风险态度和风险能力等，也是随机现象。对任何一个消费者，不能完全确定其风险态度到底属于何种，也不能完全确定其抵抗风险的能力。消费者的收入不仅由本身所提供的劳动来决定，还受到诸如能力、学识、行业、国家、地区、时期、文化等多因素的影响。

寡头厂商之间的博弈中，也属于随机现象。因为任何一个博弈都有3个基本要素：参与者、策略和支付。在每一个博弈中其参与者、每一个参与者可供选择的策略、每一个参与者所获得的各自的报酬等等，事先都不能确定，都是随机的。

所以我们可以观察到许多的社会、经济现象都是由许多微小的独立随机因素共同影响的结果。基于此，笔者认为，大量的社会现象、经济现象都是随机现象，正态分布的理论和方法广泛地适应于社会现象和经济现象的研究。

4 有关偏态和峰态的一种经济学分析和识别

“偏态”，也称偏度，是对数据分布对称性的测度。测量偏态的统计量是偏态系数，记作SK。如果一组数据的分布是对称的，则偏态系数等于0；如果偏态系数明显不等于0，则表明数据的分布是不对称的。若偏态系数大于1或者小于-1，则被称为高度偏态分布；若偏态系数在0.5～1或者-1～-0.5之间吗，则被认为是中等偏态分布；若偏态系数在-0.5～0.5之间的话，则称低度偏态分布；偏态系数越接近0，偏斜程度就越低[8]。

“峰态”，也称峰度，是对数据分布平峰或尖峰程度的测度。测度峰态的统计量是峰态系数，记作K。峰态通常是与标准正态分布相比较而言的。如果一组数据服从标准正态分布，则峰态系数的值等于0；若峰态系数的数值明显不等于0，则表明分布比正态分布更平或者更尖，通常称为平峰分布或尖峰分布。如果标准正态分布的峰态系数为0，那么当K＞0时为尖峰分布，数据的分布更加集中；当K＜0时为扁平分布，数据的分布越分散。如果标准正态分布的峰态系数为3，那么当K＞3时为尖峰分布，数据的分布更加集中；当K＜3时为扁平分布，数据的分布越分散[9]。

有关我国农村居民家庭某年度按纯收入分组的资料汇总如表1所示。

表1 我国农村居民家庭纯收入分组资料

现利用该资料计算其纯收入的偏态系数和峰态系数。为计算方便，将分组资料缩小100倍。计算过程如表2。

根据表2计算得到皮尔逊偏态系数为SK=0.571、动差偏态系数为α=0.956，并如图2所示。

所以，偏态系数为正值，而且数值较大。王长江、郝华荣等学者认为，这说明农村居民家庭纯收入的分布为右偏分布，即收入较少的家庭占多数，而收入较高的家庭占少数，而且偏斜的程度较大。[3]而笔者还认为，有一半多的家庭收入超过了平均收入，只有不到一半的家庭收入低于平均收入，这说明农村居民家庭的纯收入还是比较偏向于较高的。那些平均收入较低的家庭需要更好地考虑增加家庭收入的方法和途径，努力提高自己的家庭收入。

同理，根据上述资料计算出来的峰态系数为K=3.4，图形如图3所示。王长江、郝华荣等学者认为，这说明我国农村居民家庭纯收入的分布为尖峰分布，低收入组占较大的比重[3]。而笔者还认为，农村居民家庭的纯收入分布得比较集中，收入差距相差不大。社会和国家需要更好的收入分配机制来进行适当的兼顾效率，让努力程度不同的家庭收入分配适当拉开差距。