0-1动态数据的双向差分的模型构建

程毛林

（苏州科技学院 数理学院，江苏苏州215009）

0 引言

事物的发展大体上可分为单调型和起伏型两大类，单调型是指事物随时间递增或递减，起伏型是指事物随时间呈波动起伏。这两种情况的动态数据预测有时采用灰色预测[1～2]，其变化规律可用微分方程来表示，其中含有未知参数，预测由微分方程的解进行。估计未知参数是建立模型预测的关键，由于实际观测数据为离散的，我们将微分用差分来代替，这样微分方程变为差分方程，然后根据差分方程来估计参数[3～4]。显然微分用差分来代替会产生误差，如何减小误差，是一项重要的课题。本文给出了两种方法来减小误差，首先差分分别用向前差分和向前差分来代替微分，让前差和后差的误差平方和最小[5～6]；其次对预测的残差建立起伏型动态序列双向差分模型[7～8]以作精度修正。在平常预测中，一般对原始序列直接进行预测，但对原始序列的状态预测的研究和应用很少[9～10]，为此本文给出了0-1动态数据的双向差分建模方法。当然首先要将观测序列按某一标准转为0～1动态数据，然后建模预测。文章最后对我国国内生产总值指数变化状态作出了很好的预测。

1 0-1动态数据的双向差分建模方法

1.1 原始数据的0-1化处理

设原始序列为Y(0)={yt1,yt2,···,ytM}，其中xti为第ti年的数值，这里假定Y(0)为非负递增型时间序列，ti为等间隔。序列均值

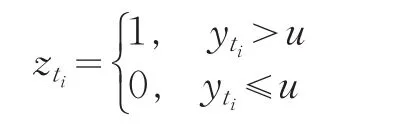
这里u为或人为标准。这样得到0-1序列:

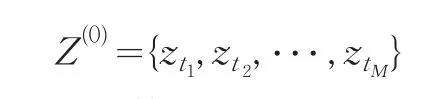
将Z(0)中“1”态出现的时间即“1”所对应的序号重新排列成一个新的时间序列：

1.2 双向差分建模方法

设时间序列X(0)={xt1,xt2,···,xtN}

对X(0)进行一次、二次乃至n次累计计算，得生成序列：

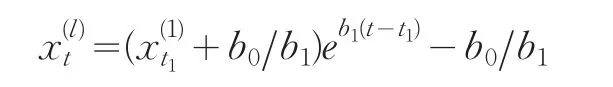
这是连续型微分方程模型，下面关键是估计出b0,b1，为此需要进行离散化。这里设：

X(0)作一次累计（即l=1)，显然x(1)t1=x0t1。

不失一般性，设时间序列为等间隔，Δt=ti+1-ti=1，由（1）式及差分和微分的关系得：

这里εt为误差。

由数值计算知，差分有向后差分：Δbx(1)tk=x(1)tk-x(1)tk-1=b0+x(1)tkb1+εbtk向后差分:

这里εbtk为向后差分代替微分引起的误差，εftk为向前差分代替微分引起的误差。让达最小，得关于b0和b1的正规方程组：

这里：

这样得到双向差分预测模型为

由估计x(1)tk，再用，还原得到原始序列，当：

k=N+1,N+2,···,N+q时可计算得到q步预测。

1.3 起伏型序列的建模

设Et={et1,et2,···,etN}为起伏型动态序列,无明显趋势。一般单调型动态序列的残差为起伏型动态序列。若动态序列Et遵从微分方程：

则可用它的解对序列进行拟合和预测，上式解为：

式中ωk为可能的周期，如时间为1到T年，可能的周期为

下面估计ak,bk。式（3）中的微分用差分代替，同时考虑等间隔，有：

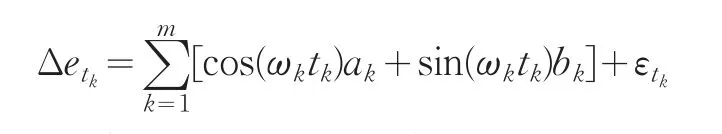
分别用向后差分和向前差分写为：

式中：

2 我国国内生产总值指数变化状态的双向差分建模

我国1996年到2010年国内生产总值指数（上年=100，不变价）序列为：

Y(0)={110.0,109.3,107.8,107.6,108.4,108.3,109.1,110.0,110.1,111.3,112.7,114.2,109.6,109.1,110.3}

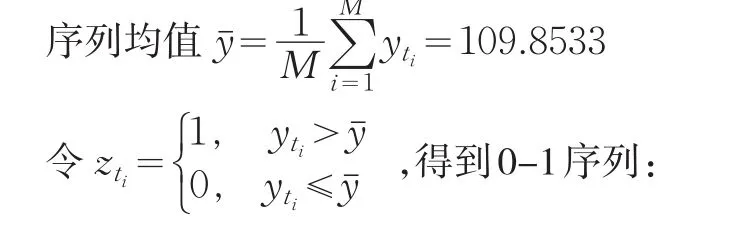
Z(0)={1,0,0,0,0,0,0,1,1,1,1,1,0,0,1}这样X(0)={1,8,9,10,11,12,15}

显然X(1)={ }1,9,18,28,39,51,66 为单调型动态序列，设满足微分方程：

由本文给出的单调型动态序列的双向差分模型建立方法，由（2）得:

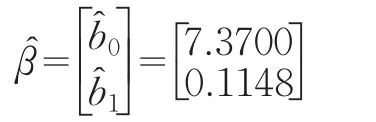
这样得到X(1)序列的双向差分预测模型为:

表1 原始数据与预测结果

X(1)序列拟合值见表1，均方根误差RMSE=0.2701，即平均相差0.2701天，平均绝对值相对误差MAPE=[0.58%]，可以看出拟合精度高。为进一步提高精度，可对X(1)序列预测残差后6项Et建立起伏型动态序列双向差分模型。

Et=[0.0685,0.1719,0.1928,-0.0006,-0.5560,0.3608]

由于观测数据是N=6为偶数，为了避免求解矩阵出现0行、0列 ，令：

设原始序列满足微分方程：

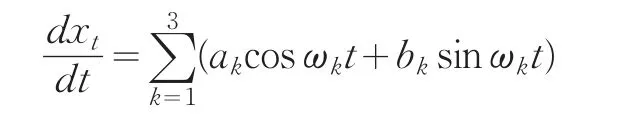
由（5）式计算可得：

进而由（4）式写得预测模型：

模型预测误差见表1，可以看出误差进一步缩小。

这样得到X(1)序列最后的预测值。用，还原得到原始序列预测值，见表1。可以看出误差极小，模型拟合效果很好。

[1] 傅立.灰色系统理论及其应用[M].北京：科学技术文献出版社,1992.

[2] Yao Tianxiang，Liu Sifeng，Xie Naiming.On the Properties of Small Sample of GM(1,1)Model[J].Applied Mathematical Modelling，2009，33（4）.

[3] 刘思峰等.灰色系统理论及其应用[M].北京：科学出版社，2000.

[4] Guo Yifan,Deng Julong.The Influence of Variation of Modeling Data on Parameters of GM(1,1)Model[J].Journal of Grey System,2004,16(1).

[5] 王学萌等.灰色系统分析及实用计算机程序[M].武汉：华中科技大学出版社，2001.

[6] 董肇君等.系统工程与运筹学[M].北京：国防工业出版社，2003.

[7] 魏风英等.长期预测的数学模型及其应用[M].北京：气象出版社，1990.

[8] 陈业华.灰色灾变预测模型及其应用[J].北京：航空航天大学学报,1998,(1).

[9] 程毛林.不等间隔动态数据的差分建模[J].数学的实践与认识,2003,(1).

[10] 蒋承仪.用双向差分及阶差鉴别法建立灰色预测模型[J].重庆建筑大学学报,1997,19(4).