云计算环境下动态数据聚集算法研究
2018-02-05,,
,,
(1.石家庄铁道大学 信息科学与技术学院,石家庄 050043;2.中北大学 电子与计算机科学技术学院,太原 030051)
0 引言
随着云计算的发展普及,云计算环境下动态数据越来越多,云计算下数据成为重要的信息资源。为了更好的利用这些资源,需要对云计算环境下动态数据进行聚集[1]。数据聚集是数据处理过程中的重要环节,对数据时代有着不可替代的作用。动态数据指在系统应用中随时间变化而改变的数据,如库存数据等,动态数据的准备和系统切换的时间有直接关系[2]。由于动态数据的变化性,导致在数据聚集过程中,数据信息存在失真甚至丢失的问题,因此云计算环境下动态数据存储首先需要解决数据可靠性问题[3]。由于动态数据所具有的独特性特征,导致传统的数据聚集算法难以满足动态数据聚集要求。这种情况下,使云计算环境下动态数据聚集算法达到最优效果,成为当前迫切需要解决的重点问题[4]。而基于同态加密与改进ECC的云计算环境下动态数据聚集算法,通过使用同态加密与消息认证码聚集密文与签名;在此基础上,对云计算中节点的动态数据进行提取,通过验证消息的完整性、发送者的合法性以及识别恶意节点,从而完成动态数据的聚集[5],这种方法有效的保证了数据的准确性及可靠性,成为这一课题的主要研究内容[6]。随着信息化发展,互联网的普及,动态数据聚集成为但仅社会研究的重点课题,随着研究的不断深入,产生了丰硕的研究成果[7]。
文献[8]提出了一种基于线性时间概率计算算法的云计算环境下动态数据聚集算法。为解决动态数据中的冗余数据,减少数据传输,提出数据聚集操作过程中,在动态数据中间节点对动态数据进行预处理,在此基础上,针对云计算环境下动态数据聚集操作路径复杂,且容易出现动态数据重复计数问题,提出通过对副本不敏感的概要结构并优化数据聚集算法特性,从而实现动态数据聚集算法。但这种算法难以保证数据的准确性。文献[9]提出了一种半监督空间化的动态数据聚集算法。针对传统数据聚集算法存在的不足,引入具备半监督学习能力的半监督项对云计算环境下动态数据特征隶属度矩阵进行增强,利用动态数据的聚类中心和中心邻近的点组成数据空间,通过动态数据的样本点与该空间的距离替代欧氏距离作为新的动态数据相似度度量标准,并给出判断聚类中心能否合并的阈值参数,从而完成半监督空间化的动态数据聚集算法,但这种算法复杂度较高,难以保证动态数据聚集前后的一致性。文献[10]提出了一种基于物理干扰模型的动态数据聚集算法,通过构造一棵根在头节点的局部数据聚集树,将整个云计算空间划分为若干个边长相等且只包含一个节点的正方形区域,最后对节点所在区域内动态数据进行聚集,但这种方法存在聚集速度较慢的问题。
针对上述产生的问题,提出一种基于粒子群优化算法的云计算环境下动态数据聚集算法,首先分析云计算环境下动态数据聚集算法数学模型,然后,提出通过粒子群优化算法完成云计算环境下动态数据聚集。通过对云计算环境中的动态数据结构模型进行分析,实现对数据的离散样本频谱特征的计算,从而完成云计算环境下动态数据聚集样本的特征提取和信息模型构建。通过混沌映射方法对其进行优化,通过生成混沌序列,解决粒子群算法存在的收敛速度慢问题,通过粒子群优化算法对云计算环境中动态数据的特征进行聚集,从而完成云计算环境下动态数据聚集算法。实验结果表明,本文所提算法是一种稳定、可靠的动态数据聚集算法,其在存储空间和准确率上均有良好的性能体现,为该领域的发展创造了条件。
1 基于最小覆盖集的动态数据聚集算法
1.1 动态数据最小覆盖集的查找以及聚集树的构造
最小覆盖集查找算法中,每个云计算节点按照云计算环境下动态数据ID升序的顺序从一跳邻居节点集AL中挑选一个未被选取的云计算环境下动态数据节点,并对该数据节点所覆盖的邻居节点中包括的二跳邻居节点集BL没有被覆盖节点个数进行判断,比较二跳邻居节点集BL没有被覆盖节点个数和AL中的其余节点个数,寻求云计算下动态数据节点数量最多;在对网络能量均衡问题进行考虑过程中,设定动态数据节点x的当前剩余能量用Ex进行表示,加入最小覆盖集的动态数据节点阈值利用Ethreshold进行表示,则有Ex>Ethreshold,只有当数据节点同时满足Ex>Ethreshold条件的同时动态数据节点数量最多,才可以加入云计算环境下动态数据的最小覆盖集中,随着时间的推移,Ethreshold阈值随着云计算网络能量的变化而动态的发生变化,从而适应最小覆盖集算法的需求,实现对云计算环境下动态数据最小覆盖集的查找。
再次基础上,对动态数据聚集树进行构造,在进行动态数据聚集树构造过程中,通过云计算环境下动态数据的最小覆盖集查找方法,得到MCS,在此基础上,向外广播动态数据聚集树,完成包含MCS的数据节点列表的动态数据信息ATC的构建,当动态数据节点收到ATC消息后,执行最小覆盖集转发算法,其具体过程如下所述。
对云计算环境下动态数据节点接收ATC次数进行判断,如果不是第1次接收ATC,则终止算法,如果是第1次接收ATC,则可以利用该云计算环境下动态数据节点的邻居节点进行下一跳转发,并对该节点是否属于MCS中的节点进行判定,如果不属于MCS节点,则终止算法,否则,对该节点的MCS进行计算,继续广播,重复上述步骤,直至在云计算环境下动态数据的每个层都产生一个MCS,且以Sink为根的树。MCS中的节点覆盖次序与查找算法中依次加入的次序相同,也就是说覆盖次序与覆盖BL中数据节点数量相关,在进行下一次对ATC的覆盖前,需要在一段适合的时间后,从而避免多个节点同时覆盖过程中存在相同MCS邻居节点产生的碰撞;此外,当动态数据节点收到来自上层节点的相同ATC信息,则选择较早的覆盖节点作为自己的下一跳转发节点。
1.2 数据聚集算法
针对云计算环境下动态数据中间节点,利用读向量相似性的方法去除其冗余和错误数据信息,通过读向量的形式将正确的云计算环境下动态数据发送到下一个动态数据的中间节点,通过数据缓存窗口Δt内的一系列读数对云计算环境下动态数据节点Ni的读向量进行描述,Ri={xi(t-Δt+1),xi(t-Δt+2),…,xi(t)}表示云计算环境下动态数据节点Ni的读数,其中,xi(t)表示动态数据节点Ni在t时刻的数据采样值。节点Ni在缓存窗口Δt内的读数代表一个读向量。
由于云计算环境下动态数据在正常情况下是渐变且有趋势的,而错误数据信息会改变数据变化的趋势,或当前数据发生跳跃,为发现这种错误数据信息,通过读向量相似系数ρ对动态数据进行判断。
(1)
式中,E(X)表示读向量的数学期望,E(X)表示读向量的方差,ρXY∈[-1,1]。|ρXY|与XY之间误差成反比关系,随着|ρXY|的增大,误差逐渐减小,冗余性提高;反之,则说明该读取向量中存在错误信息。通过在数据聚集时设置一个云计算动态数据中间节点阈值θ,当ρXY<θ时,认为该动态数据为错误数据,将其放入错误数据集,在算法完成后,丢弃错误数据集;否则,将云计算数据放入冗余数据集,并求取冗余数据集的平均值,将结果发送到下一个动态数据聚集节点,反复上述操作,直到完成对所有云计算下数据聚集,从而实现云计算环境下动态数据聚集算法。
2 基于粒子优化群算法的动态数据聚集算法
2.1 云计算环境下动态数据聚集算法数学模型
设待聚集的云计算环境下动态数据的样本空间为X={x1,x2,…,xn},其中云计算环境下动态数据样本xi=(xi1,xi2,…,xip)(i=1,2,…,n)表示P维特征空间RP中的一点。聚集问题可以表示成找到一个划分C=(C1,C2,…,CK),满足公式(2),并使得总的类间距离和最小。类间距离和用公式(3)进行计算。
(2)
(3)

2.2 基于粒子群优化算法的动态数据聚集算法
在上述云计算环境下动态数据聚集模型的基础上,提出通过粒子群优化算法的云计算环境下动态数据聚集算法。
设定一个D维动态数据聚集搜索空间,存在一个由m个粒子组成的粒子群,每个云计算环境下动态数据信息特征矢量Ai对应的函数可以表示成:
li(k)=(1-ρ)li(k-1)+γf(xi(k))
(4)
式中,fi表示Ai模因组适应度函数,xi(k)表示第i个粒子k时刻的全局优化粒子权值。
设置门限值Nth,当Neff xk+1=sin(a/xk),0<|xk|≤1 (5) 式中,xk表示云计算环境下第k个动态数据的惯性权重;a表示动态数据聚集中心的控制参量。 ∑τ=diag(max(σi-τ,0)) (6) 根据不同的动态数据聚集任务,对适应度函数内权重进行调整,得到新的聚集权重系数可以表示为: (7) 式中,{α,β}表示云计算环境下动态数据聚集的分集聚敛目标函数,从而得到优化的聚集目标函数可以表示为: (8) 其中:粒子的位置对应云计算环境下样本数据的k个聚类中心。除了粒子位置外,对粒子的适应度和速度进行编码。由于样本数据的属性向量维数为d,则粒子的位置和速度为k×d维矩阵。 针对粒子群算法进行动态数据聚集存在的早熟并且收敛速度慢的问题,本文通过混沌映射方法对其进行优化,混沌方法首先要生成混沌序列,混沌序列可以表示为: Zn+1=μZn(1-Zn) (9) 随着粒子群的不断进行迭代计算,当其计算超过一定阈值,粒子群算法收敛速度开始下降,为了解决这一问题,利用生成的混沌序列来对全局最优粒子进行扰动。将上述云计算下动态数据的m个粒子的每一维度在(0,1)范围上一一映射,从而得到向量D=(d1,d2,…,dm)。其中,d1表示粒子第i维,其表达式可以表述为: di=(gbesti-a)/(b-a) (10) 式中,gbesti表示动态数据粒子中适应度最高粒子的第i维;a和b分别表示动态数据粒子在任意维度中的取值下限和上限。 利用混沌扰动重新对云计算环境下动态数据进行迭代计算,得到新序列: Z1=(Z11,Z12,…,Z1m) (11) 将上式计算得到的新序列Z1当成云计算环境下动态数据的新粒子,并进行适应度计算,与之前搜索得到的最优解适应度相比,如果计算得到Z1适应度更高,则可以说明Z1为当前最优解。 通过上述论述,在云计算环境下动态数据聚集表示一个任务调度策略,从而完成基于粒子群优化算法的云计算环境下动态数据聚集算法。 为了证明本文提出的基于粒子群优化算法的云计算环境下动态数据聚集算法的有效性和实用性,以Intel P4 2G处理器为硬件环境,MATLAB2008a为平台,运用对比法将本文提出的基于粒子群优化算法的云计算环境下动态数据聚集算法与文献[8]和文献[9]所提云计算环境下动态数据聚集算法进行比较,完成本次实验。 1)对比3种云计算环境下动态数据聚集算法的复杂度; 2)改变云计算环境下动态数据大小,得到不同大小数据聚集时间对比; 3)对比各方法下不同大小动态数据聚集所占空间; 4)通过对比数据聚集后的原始性,比较3种云计算环境下动态数据聚集算法的可靠度,; 5)对3种云计算环境下动态数据聚集算法的能耗(焦)进行对比。 首先对比3种云计算环境下动态数据聚集算法的复杂度,设算法的复杂度单位为%,其计算方法如公式(12)所示。 (12) 式中,n表示算法的循环次数,通过计算,得到3种算法的复杂度对比,对比结果如图1所示。 图1 3种算法的复杂度对比 通过图1可以看出,本文所提算法的复杂度较文献[8]和文献[9]低,说明本文所提算法的复杂度较低,算法执行较为简单,且利于后续维护工作的开展。 表1是云计算环境下不同大小动态数据聚集时间(s)对比。通过改变云计算环境下动态数据大小,得到不同大小数据聚集时间对比。 表1 不同大小数据聚集时间对比 通过对表1的分析可知,本文采用粒子群优化算法,改善粒子群算法进行数据聚集存在的收敛速度慢问题,提高了数据聚集时间,证明本文所提方法具有较好的可行性。表2是3种算法对不同动态数据进行数据聚集所占的空间(MB)对比,通过实验不同大小动态数据聚集所占空间,完成该实验。 表2 3种算法数据聚集所占存储空间对比 通过表2可知,本文所提算法在进行数据聚集时,数据所占内存变化较小,说明本文所提算法进行数据聚集,能够较好的保证数据的原始性,也就是说,本文所提算法能够较好的保证数据的准确性。 对比3种云计算环境下动态数据聚集算法的可靠度,设可靠度单位为%,通过对比数据聚集后的原始性,完成本次试验。通过实验,得到3种算法的可靠度对比,对比结果如图2所示。 图2 3种算法的可靠度对比 通过对上图的分析可知,本文所提方法由于在进行云计算环境下数据聚集之前,首先构建了数据聚集算法的数学模型,使本文所提云计算环境下动态数据聚集算法的可靠度与文献[8]和文献[9]所提算法可靠度相比,有了较大幅度提高,且本文所提算法的可靠度较稳定。 最后对3种云计算环境下动态数据聚集算法的能耗(焦)进行对比,通过实验,得到3种云计算环境下动态数据聚集算法的运行能耗对比,对比结果如图3所示。 图3 3种算法的运行能耗对比 通过图3可知,本文所提算法的运行能耗较少,由于本文所提算法可靠度较为稳定且进行数据聚集的时间较短。 综上所述,本文所提云计算环境下动态数据聚集算法能够有效提高数据聚集的可靠度,降低数据聚集时间及能耗,且数据聚集占用的内存较少,数据聚集算法的复杂度较高,具有良好的使用价值。 随着云计算的普及,云计算数据越来越多,对云计算环境下的数据进行聚集成为新的关注热点。传统的云环境下动态数据聚集算法由于其动态复杂度高,且收敛速度慢等问题,提出一种基于基于粒子群优化算法的云计算环境下动态数据聚集算法。并通过实验证明,所提方法能够有效提高云计算环境下动态数据聚集算法的数据聚集时间较短,且其复杂度较低,是一种可靠、节能、稳定的数据聚集算法,对云计算环境下动态数据管理起着积极作用。 [1] 林国勇,黄 帆.一种用于云计算的数据容灾分配算法的改进[J].科学技术与工程,2017,17(1):260-264. [2] 李晓峰.云平台中大数据并行聚类方法优化研究仿真[J].计算机仿真,2016,33(7):327-330. [3] 张 宇.基于极值特征的雷达侦察数据BIRCH聚类方法[J].电子设计工程,2016,24(9):15-18. [4] 解 锋,叶晓慧.一种数据特征敏感的高效数据聚集编码方案[J].计算机测量与控制,2016,24(3):179-182. [5] 龙 虎,张小梅.基于修正二阶锥规划模型的大数据聚类算法[J].科技通报,2016,32(8):168-171. [6] 周永正,张金良.聚集数据多元线性模型参数的多元聚集广义岭估计的相对效率[J].数学的实践与认识,2016,46(9):149-155. [7] 范凌云,文国琴,张文涛.VANET中基于认知代理与回归聚集的低延迟数据处理算法[J].计算机应用研究,2016,33(6):1871-1876. [8] 应可珍,邬锦彬,戴国勇,等.一种基于线性时间概率计数算法的数据聚集技术[J].传感技术学报,2015,28(1):99-106. [9] 于 平,王士同.半监督空间化竞争聚集算法及其在图像分割中的应用[J].计算机工程,2015,41(2):234-241. [10] 刘文彬,刘红冰,李香宝,等.基于物理干扰模型的无通信冲突的数据聚集调度算法[J].计算机应用研究,2015,32(7):2092-2096.3 实验及结果分析
3.1 实验步骤
3.2 实验结果分析



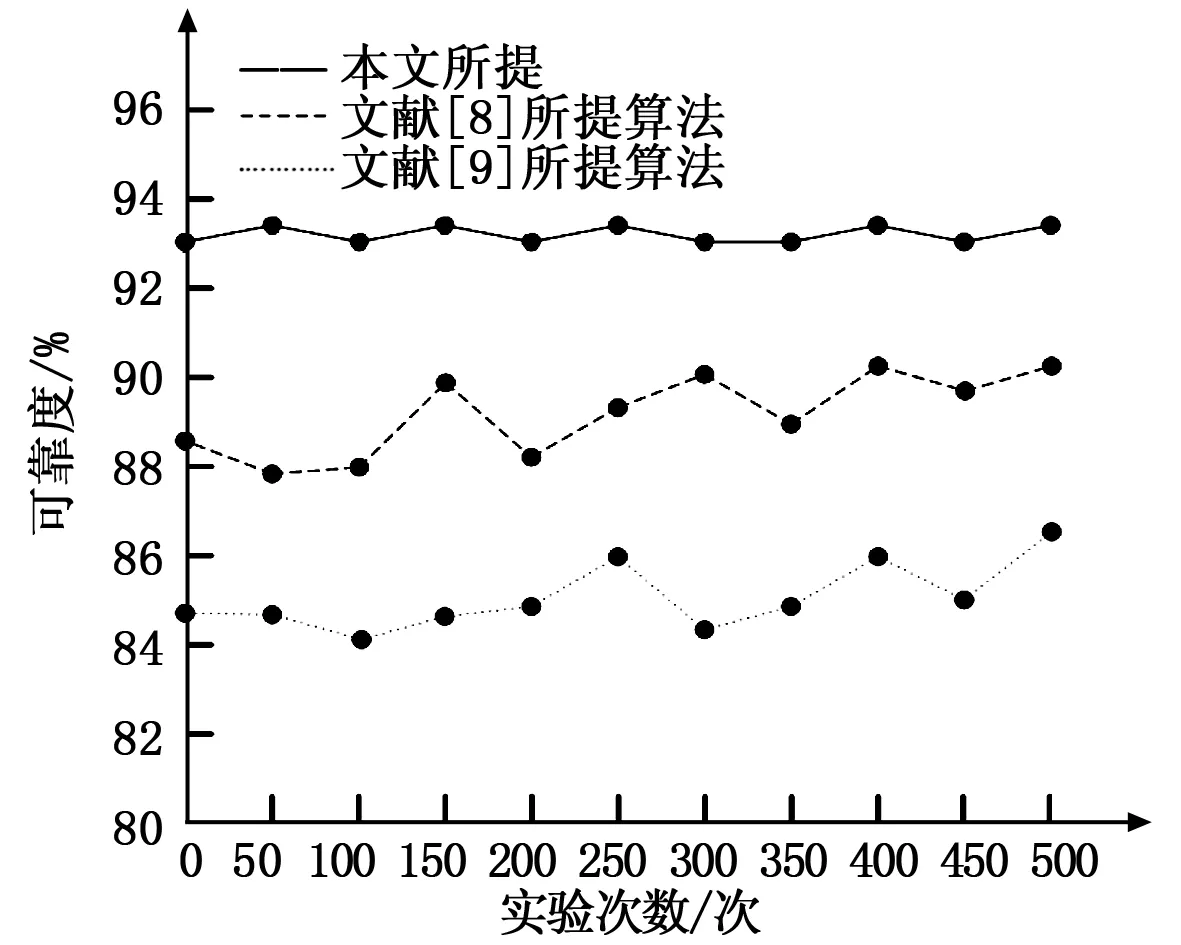

4 结束语
