弹性需求下的闭环供应链收入费用共享契约研究

徐 红，施国洪

(1.江苏大学工商管理学院，江苏 镇江212013;2.盐城工学院经济管理学院，江苏 盐城 224001)

O 引言

闭环供应链是对正向和逆向供应链的有机集成。现在正越来越成为一个热点研究领域。目前大多数闭环供应链的研究文献属定性分析，为数不多的定量分析也集中在闭环供应链物流网络的设计、库存控制、回收和再制造等领域。不同于以往大多数文献只考虑确定需求信息下正向或逆向供应链，本文试图从不确定需求，且需求受到价格影响的角度，以闭环供应链全局的视野，利用博弈论这个工具来探讨由一个制造商和一个零售商组成的二级闭环供应链的定价问题以及成员之间的合作。不确定需求信息且把零售价格作为内生变量的假设更加符合闭环供应链的实际运作，因此本文的研究对闭环供应链的实施具有一定的指导意义。

1 问题描述和模型的基本假设

决策过程如下：

本文的研究对象是由一个制造商和一个零售商组成的二级闭环供应链，供应链中制造商负责新产品的制造和回收产品的再制造，零售商负责产品的销售和废旧产品的回收，两者的博弈过程为：制造商提供契约形式决定产品的批发价和废旧产品的回收价格，零售商根据制造商的契约来决定产品的市场销售价格、废旧产品的市场回收价格以及产品的订购数量。

基本假设：

（1）制造商利用原材料生产新产品的单位成本为CM，利用回收材料生产再造品的单位成本为CI，并设CM＞CI，CM 、CI均大于零,制造商对所有回收的废旧品进行加工处理，形成再造品，即没有任何废弃处理。

（2）制造商以批发价W提供该产品（包括新产品和再造品）给零售商，零售商再以零售价U提供给消费者，再造品与新产品在质量、功能上是一致的，消费者对再造品和新产品具有同样的认可度,制造商委托零售商销售并回收该产品，制造商回收产品的单位价格为P1,零售商的市场回收价格为P2，零售商回收废旧产品的单位成本为Cr。

（3）假设产品的市场需求是随机的设其需求函数D，在表示需求的不确定性上文献提出了两种表示方法:一种是加性不确定性,一种是乘性不确定性。本文采用后一种方法，将用乘法的形式来表示，即D=aU-b*ε，其中ε为随机变量，f(x)是其概率密度函数，F(x)是其分布密度函数，可微且单调递增，其逆函数存在且单调递增。

（4）假设废旧产品的市场回收量S=tPK2,其中 t为换算常数，k为市场价格弹性。

（5）由于市场需求的不确定性,假设销售不出去的剩余产品的单位残值为V,不考虑不能满足市场需求造成的缺货费用（事实上，考虑缺货费用只能使模型结构变得更复杂，并不会改变问题的实质）

（6）制造商和零售商均为独立的决策者，均为风险中性者，不考虑风险偏好引起的风险成本，同时二者都是以利润最大化为各自的目标。

πM、πR和π分别表示制造商的利润、零售商的利润和整个闭环供应链系统的利润。为保证闭环供应链能正常运作，使上述假设有意义，W≥CM,CM-CI≥P1,P1≥P2+Cr根据上述模型的假设:

用S(Q)表示零售商的期望销售量，则:

S(Q)=min(Q,D)=aU-bmin(δ,ε)

2 合作博弈集中决策的定价模型

在集中决策的定价模型中，制造商负责产品的生产、销售和回收。此时，制造商和零售商作为一个整体，追求的是整个闭环供应链系统利润的最大化。但由于市场需求的不确定性，制造商独自承担需求不确定性所带来的过剩或缺货风险。根据前面的假设，则合作博弈下集中决策时整个闭环供应链系统的利润。

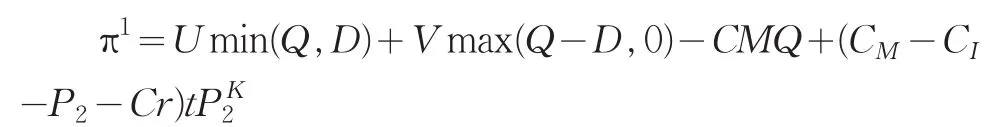
根据文献，令Q=aU-b*δ，由于ε是随机变量，所以整个闭环供应链系统的期望利润为:

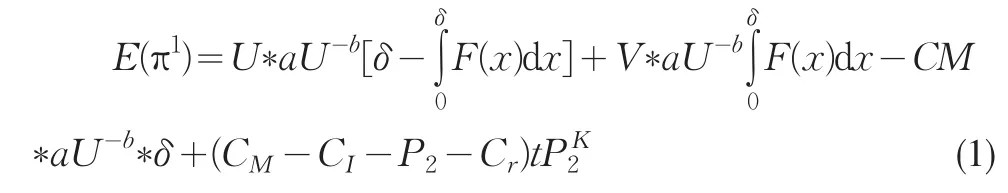
对(1)分别求关于U和δ的偏导，得到:

分别令(2)(3)等于零，得到:

对(1)求P2的偏导数，得到

将(4)(5)(6)联立起来就可得到集中决策下闭环供应链各决策变量的最优解。即:

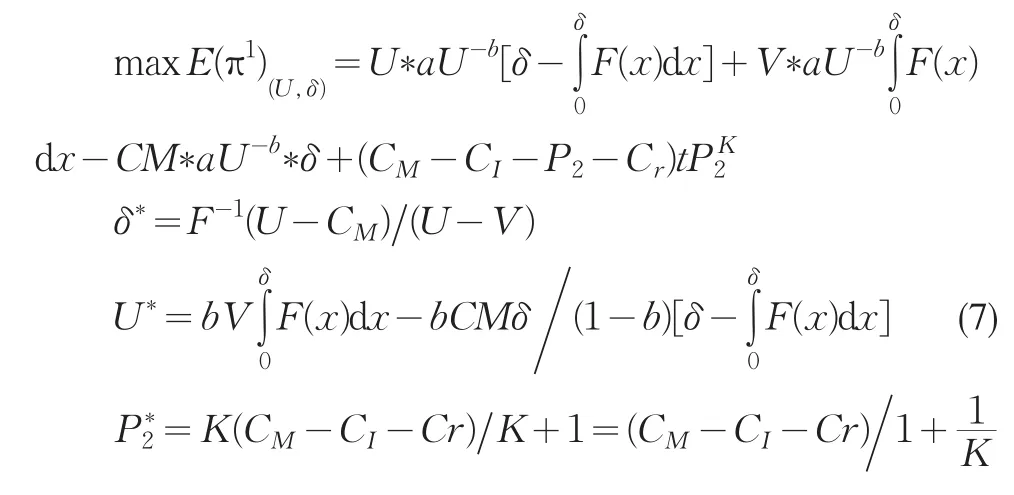
3 非合作博弈分散决策的定价模型

非合作博弈分散决策是指由于利益的主体不同，各自以追求利润最大化为目标。本文在文献[2]的基础上讨论制造商负责生产，零售商负责销售并进行回收的模式。假设制造商为主导者,销售商为跟随者,即制造商首先决定新产品和再造品的批发价格W，以使自己获得的收益最大,销售商随即对此做出反应,确定新产品和再造品的市场零售价格U,同样也使自己的收益最大。这样双方就构成了stackelberg模型。此时，由于制造商是根据零售商的订货量来进行生产，因此不需要承担市场不确定需求所带来的风险，而零售商这时直接面对市场，不得不承担需求不确定性所产生的过剩或缺货风险。根据文中的假设，则制造商和零售商的利润分别为：

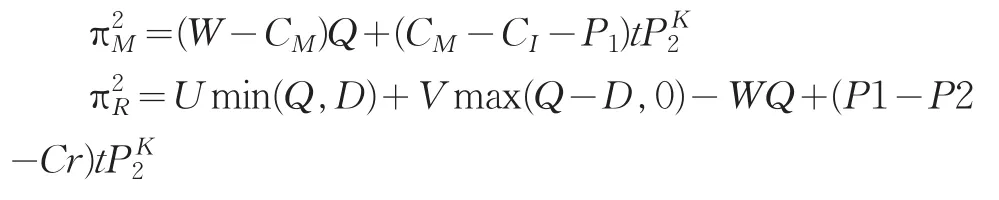
那么制造商和零售商的期望利润分别是：

由逆向归纳法，对(9)中分别求δ和U 的偏导数,得到同样也对(9)求P2的偏导数，得到:

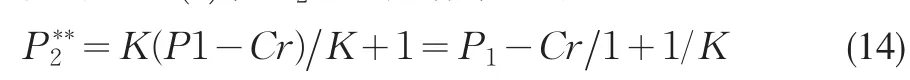
根据零售商的反应函数，制造商决定令π2M最大化的W**和回收废旧产品的价格P**1，则有:

求解（15），就能得到各决策变量的最优解。

4 协调机制的形成

结论1：由于U-W≤U-CM,且 F(x)单调递增，因此δ**≤δ*,也就是说在分散决策下，零售商的订货量并没有达到系统的最优订货量。

结论2：由于W≥CM,比较⑸和⒀可以发现，在分散决策下，零售商的零售价格要高于集中决策下的零售价格。

结论3：由于CM-CI≥P1,比较⑹和(14)可以发现，在分散决策下，废旧产品的回收价格要小于集中决策下废旧产品的价格，那么废旧产品的回收量就会减少，零售商回收的积极性就会减弱，社会资源就可能出现浪费。

结论4：在集中决策下，零售商的最优市场回收价格只与K,CM-CI有关，且是关于K,CM-CI的增函数。

分析表明，由于双重边际效用的影响，非合作博弈分散决策不是最优决策，集中决策可以降低系统成本，这需要零售商增加订货量，而此举会增加零售商的成本。由于双重边际现象的存在，在非合作博弈的模式下，由制造商和零售商各自以利润最大化为目标的整个闭环供应链系统利润小于合作博弈模式下的整个闭环供应链系统的利润，也就是说供应链系统的效率降低了，同时也说明了制造商和零售商通过合作可以提高各自的利润以及整个系统的利润，为此，根据信息经济学的委托——代理理论，设计一种契约，协调双方，促使双方形成一种合作机制，而收入费用共享协调机制能符合这种契约的要求。收入费用共享的协调机制是在传统的收入共享契约的基础上加以改进的，是指以较低的批发价出售给零售商，同时要分享零售商的一部分销售收入，但是由于是闭环供应链，零售商回收废旧产品要产生一些回收费用，因此制造商在分享零售商的一部分销售收入的同时，还要以相同的比例分担零售商的一部分回收费用。

根据上面的分析模型如下：

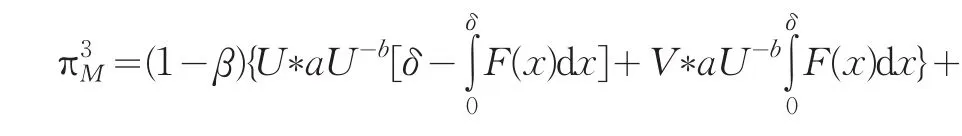
供应链总利润为:

模型求解与分析:

为实现协调，使零售商的最优订货数量与废旧产品的最优回收价格和合作博弈集中决策相一致，因此对⒄分别求δ和P2的导数得到：

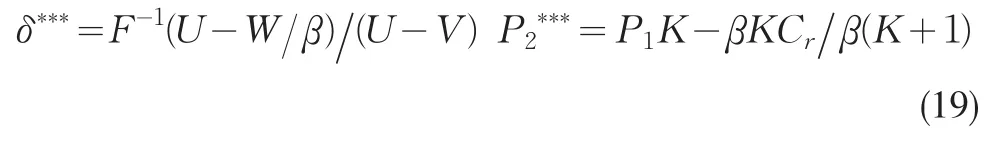
将(19)与(4)(6)比较发现，要实现协调，必须使

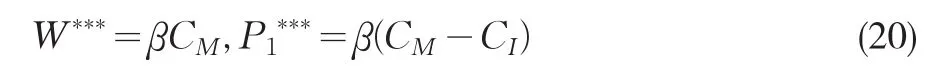
与此同时，在进行收入费用共享的协调机制时，还必须满足下列条件，即：将上式代入得到

通过比较发现，经过收入费用共享的协调机制后，闭环供应链系统实现了完美协调。

5 模型的数字算例

为了进一步地说明模型的应用，下面通过对模型的各参数进行赋值来求得各模型的最优决策解。

取a=100,b=2,CM=10,Cr=2,CI=4,V=2,t=0.5,K=3,ε(0,2)利用LINGO8.0数学软件进行数值仿真,把各参数代入到式(7)、（15），求得各模型的最优解，即集中决策下模型的最优解为U*=28.6,δ*=1.3985,P*2=3,E(π1)=15.0901,非合作分散决策下模型的最优解为W=19.534,U**=57.23,δ**=1.3651,E(π2R)=5.0570,E(π2M)=5.9863,0.34≤β≤0.60下面通过表格来比较进一步说明本文的结论。

表1 集中决策与分散决策模型时的均衡结果

从表1中的结论中可以看出,在分散决策下,零售商的最优订购量并没有达到集中决策时的订购量,同时也可以看到,无论是废旧产品的回收价格,还是整个供应链系统的总利润均要小于集中决策下相应的结果,只不过是在分散决策下,零售商的零售价格要高于集中决策时的零售价格,这些正与本文的结论1,2,3一致。

表2 协调机制下制造商和零售商利润的变化

从表2中可以发现，β越大，制造商的利润越小，零售商的利润越大，β越小，制造商的利润越大，零售商的利润越小，因此，β的取值如何要取决于双方的讨价还价能力。

6 结语

本文研究了由一个制造商和零售商组成的二级闭环供应链的定价及协调问题，构建了在不确定需求条件下由一个制造商和一个零售商组成的闭环供应链定价模型，并运用博弈论揭示了在面对市场不确定需求的情况下，供应链的节点企业如何定价，设计契约，得出一系列有意义的结论。研究表明，在闭环供应链中，各节点企业应加强信息的共享和合作，通过合作不但增加了各节点企业的利润，而且也增加了整个闭环供应链系统的利润，提高了供应链系统的效率。

（1）本文是以一个制造商和一个零售商组成的二级供应链为研究对象，如何构建多级供应链在不确定需求下的定价和协调机制是今后的研究方向之一。

（2）本文是假设制造商和零售商都了解对方信息即对称信息的前提下得出的相关结论，而在不对称信息的情况下，会更加复杂，这也是本文进一步研究的方向。

[1] G.Cachon.Supply Chain Coordination with Contracts.Technical Re⁃port,the Wharton School of Business[C].University of Pennsylbania,Philadelphia,PA,2002.

[2] 李新军,林欣怡,达庆利.闭环供应链的收入共享契约[J].东南大学学报(自然科学版)2008,38（3）.

[3] 葛静燕,黄培清.基于博弈论的闭环供应链定价策略分析[J].系统工程学报,2008,23（1）.

[4] 王玉燕,李帮义,乐菲菲.两个闭环供应链的定价模型研究[J].预测,2006，(6).

[5] 索寒生，金以慧.两阶段供需链企业间的博弈分析[J].计算机集成制造系统，2003，9(7).

[6] 张维迎.博弈论与信息经济学[M].上海:上海人民出版社,1996.

[7] 姚卫新.再制造条件下逆向物流回收模式的研究[J].管理科学,2004,17(1).