基于齿轮动态激励和弹流润滑的多目标优化
2012-07-09钱学毅
钱学毅, 吴 双
(1. 武夷学院电子工程系,福建 武夷山 354300;2. 浙江经贸职业技术学院应用工程系,浙江 杭州 310018)
齿轮传动系统的刚度激励表现为因啮合齿对数变化导致啮合综合刚度随时间周期变化从而引起齿轮轮齿啮合力周期变化。刚度激励是一种参数激励,其力学效应使齿轮系统处于参数振动状态。这样,即使外载为零或为常量时,系统也会因刚度激励而产生振动。刚度激励主要与齿轮副的设计参数有关[1]。因此,从刚度激励和系统行为的统一性方面研究系统参数与结构的优化选择与配置,有助于改进齿轮传动系统的设计。
在对齿面胶合强度的计算中,冷胶合是指因为载荷过大使油膜破裂,出现金属直接接触的破坏现象。主要发生在处于边界或混合润滑状态下的重载齿轮传动中,通常用控制齿间最小油膜厚度的方法避免齿面冷胶合。齿间最小油膜厚度越大,齿面胶合强度越高。根据弹性流体动力润滑理论和现代磨擦学理论,齿间最小油膜厚度与齿轮的设计参数密切相关。因此,合理选择齿轮的设计参数,有助于提高齿面胶合强度。
目前国内外针对齿轮传动系统刚度激励及齿间最小油膜厚度的研究日益受到人们的关注,取得了一定的进展。文献[2,4]通过对行星轮系建立系统动力学方程,对系统中时变刚度引起的激励及对系统振动的影响进行了系统的研究。文献[5]建立的行星齿轮传动的弯扭耦合非线性动力学模型考虑了诸多因素的影响,其中也包括时变刚度。文献[6]在对风力发电齿轮传动系统参数优化设计中也考虑了时变刚度对动载系数的影响。文献[7]在用弹流润滑理论计算齿间最小油膜厚度方法的基础上,利用计算机仿真技术探讨了齿面胶合失效的模糊性。文献[8]依据弹性流体动力润滑理论,以齿间最小油膜厚度最大和齿轮传动总体积最小为目标函数,进行了约束两目标优化设计。迄今为止,同时以齿轮啮合时变刚度激励最小、齿间最小油膜厚度最大(倒数最小)及齿轮传动总体积最小的3目标最优化研究尚未见有论文发表。
本文对目前用于2目标优化设计的粒子群优化方法进行了改进,给出了约束3目标优化设计方法。从现代齿轮系统动力学基本原理和弹性流体动力润滑理论出发,建立同时追求齿轮啮合时变刚度激励最小、齿间最小油膜厚度最大及传动总体积最小的约束3目标最优化设计数学模型。利用Matlab进行优化程序设计,举例说明了分析计算的一般方法。为指导高质量齿轮系统的设计与制造提供有价值的参考。
1 齿轮系统的动态激励与轮齿啮合综合刚度
1.1 齿轮系统的动态激励
齿轮传动系统作为一种弹性的机械系统,在动态激励作用下产生动态响应。齿轮系统的动态激励有内部激励和外部激励两类,其中与一般机械系统的主要不同之处在于它的内部激励。内部激励是指由齿轮副轮齿啮合过程中所产生的动态激励。一般说来,齿轮轮齿啮合的重合度大多不是整数,啮合过程中同时参与啮合的齿对数随时间而周期变化,导致轮齿啮合刚度随时间周期变化。由于同时啮合齿对数的变化,引起了啮合过程的轮齿动态啮合力。刚度激励则是因啮合刚度的时变性产生动态啮合力并对系统进行动态激励的现象,是内部动态激励的主要形式之一。
1.2 轮齿啮合综合刚度
轮齿啮合综合刚度是指在整个啮合区(图1中的A―D段)中,参与啮合的各对轮齿的综合效应,主要与单齿的弹性变形、单对轮齿的综合弹性变形以及齿轮重合度有关。
单齿的弹性变形是单个轮齿的啮合面在载荷作用下的弹性变形,其中包括了弯曲变形、剪切变形和接触变形等。图1(b)中的δp和δg分别为啮合区中单个的主、被动轮齿的变形曲线。
单对轮齿综合弹性变形是指一对轮齿在啮合过程中弹性变形的总和,用δs表示

由于主、被动轮齿分别是在齿顶与齿根和齿根与齿顶相互啮合,因此,叠加后的弹性变形曲线如图1(b)中的 δs。
主、被动齿轮的相互啮合,相当于两根弹簧的串联。因此,单对轮齿综合啮合刚度ks为

式中 kp和 kg分别为主、被动轮齿的单齿刚度,即

对于轮齿啮合综合刚度,如图1(d)所示,在双啮合区,有两对轮齿同时参与啮合,相当于弹簧的并联,双齿啮合综合刚度等于单齿啮合综合刚度之和,刚度曲线是两对轮齿综合刚度的叠加,可以看出,轮齿啮合综合刚度具有明显的阶跃型突变性质。
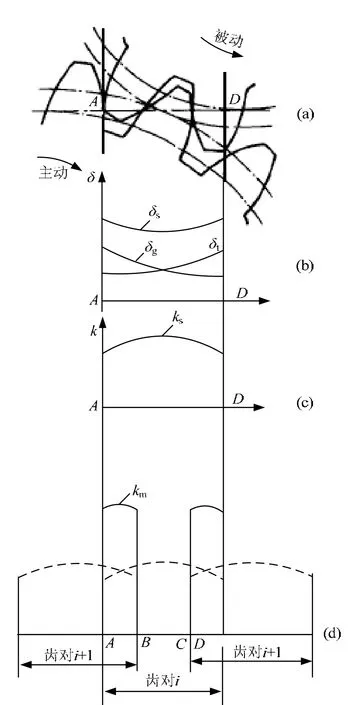
图1 轮齿啮合综合刚度
1.3 刚度激励的优化
由于轮齿啮合综合刚度类似于方波周期函数,可以将其展开成傅里叶级数,相应的谱图具有多次谐波成分。在频域中,若频率成份简单,相应的幅值大,则啮合的刚度激励较弱。又因为基频谐波的幅值对刚度激励的影响最大。因此,可以通过齿廓参数的优化设计,以频域中轮齿啮合综合刚度谱图中基频谐波的幅值最大化作为目标,来达到弱化刚度激励的目的。
将轮齿啮合综合刚度按啮合频率简化成矩形波周期函数,再将其展开成傅里叶级数并略去高阶项后整理得[9]
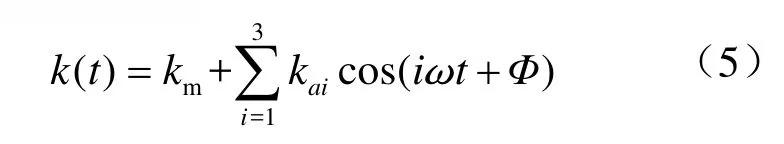
式中,km——平均啮合刚度;
kai——变刚度幅值系数;
ω——啮合频率,ω =πnz/30;
n,z,Φ——转速、齿数及相位角。
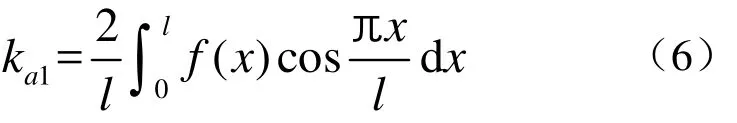
按式(6)计算基频谐波的幅值时,首先按GB/T3480―1997计算单齿啮合刚度 C,然后根据重合度ε分单齿啮合和双齿啮合两个阶段进行积分。单齿啮合时, f(x)=c,双齿啮合时,f(x) =2c。轮齿优化时,以基频谐波幅值ka1最大作为追求的目标函数之一。
2 齿间最小油膜厚度的计算
1987年,我国著名磨擦学家杨沛然和温诗铸在深入研究 Dowson-Higginson膜厚公式的基础上,根据Roelands粘压关系和采用复合直接迭代解法,对于较广泛的速度和载荷变化范围内的线接触弹流润滑问题求得收敛解,进而回归出比Dowson-Higginson膜厚公式更为准确、合理的最小油膜厚度公式[10]
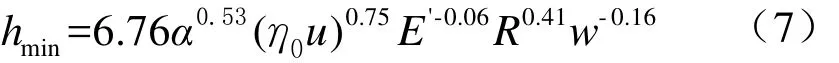
式中:
hmin——最小油膜厚度,mm;
α ——润滑油的粘压系数,1/MPa;
η0——润滑油在某温度下的动力粘度,
MPa.S;
u——齿面平均速度,mm/s;
E'——齿轮材料综合弹性模量,MPa;
R——节点处的当量曲率半径,mm;
w ——单位接触宽度载荷,N/mm。
3 非对称直齿轮约束多目标粒子群优化设计
非对称齿轮是在工作齿面设计一个较大的压力角,非工作齿面设计一个较小的压力角。这样,即可以提高齿轮的承载能力又可以有效地避免齿顶过分变尖的现象[11]。
齿轮的啮合综合刚度越大,动态激励越小,齿轮的动态性能越好;齿间最小油膜厚度越大,胶合强度越高;齿轮传动总体积越小,经济成本越低。这是一个约束3目标优化问题。3个目标没有公度性,不宜用传统的多目标优化方法进行处理。这是因为传统的多目标优化方法是将 3个子目标(轮齿啮合综合刚度最大、齿间最小油膜厚度最大及齿轮传动总体积最小)通过权重的设置聚合成一个带正数的单个目标函数,系数由决策者决定,或者由优化方法自适应调整。传统方法在处理这类问题时存在着如下缺陷:
1)啮合综合刚度的单位是N/(mm.μm),齿间最小油膜厚度的单位是mm,齿轮传动总体积的单位是mm3,3个目标的单位不一致,无可比性。
2)通过权重的设置将多目标问题转化为单目标问题,带有较浓重的主观色彩,难以反映客观真貌。权重的设置要求设计者有长期的研究经验和厚重的领域知识,稍有偏差就会大大影响多目标最优解的产生,因此合适地选取权重是一个难度较大的过程。
3)一次运行通常只能得到一个Pareto最优解,而多次运行得到的优化结果可能不一致,很难进行有效的决策,导致不能得到Pareto最优解集。
4)各子目标函数之间通过决策变量相互制约,存在相互矛盾,致使加权目标函数的拓朴结构十分复杂。
粒子群优化算法(particle swarm optimization,PSO)[12-13]在解决约束多目标优化问题中得到有效应用。在文献[14-15]中提出的寻优原则和搜索方法基础上,给出本文范例约束3目标粒子群优化算法。算法并非将3个子目标函数通过权重的设置聚合成为一个单目标进行优化,而是首先在设计变量可行域初始化一个粒子群体,然后通过各个子目标函数共同指导每个粒子在设计变量可行域中向3个目标函数不同时增大的方向一步步搜寻,最终使粒子落入非劣最优目标函数空间。具体实现要点如下:① 以频域中轮齿啮合综合刚度谱图中基频谐波幅值的倒数f1(X)、最小油膜厚度的倒数 f2(X)及齿轮传动总体积 f3(X)中的每个目标函数,找到粒子群体中相对应的全局极值G[j](其中j = 1,2,3是目标函数的个数)和每个粒子的个体极值P[i,j](其中i = 1,2,…,N是粒子群体中的粒子个数)。② 在更新每个粒子的速度(相当于有向步长)时,用各个G[j]的均值g作为全局极值。③ 每个粒子的个体极值P[i,j]是通过判断矢量P[i,j]相对于矢量G[j]的离散程度来决定,是取P[i,j]的均值,还是在P[i,j]中随机选取。
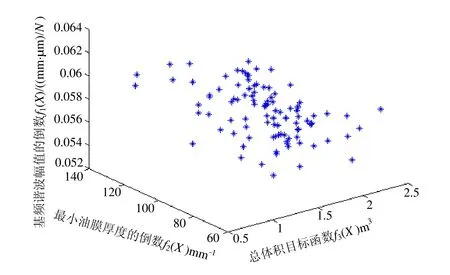
算法流程如下:① 给定算例粒子群规模N ,在约束条件允许的可行域内随机产生各粒子的位置Xi和速度Vi(i = 1,2,…,N )。② 用目标函数 f1(X)、f2(X)和 f3(X)分别计算每个粒子的适应度值。③ 在f1(X)、f2(X)和f3(X)下分别对每个粒子求得个体极值。④ 对f1(X)、f2(X)和f3(X)分别求3个全局极值。⑤ 计算3个全局矢量的均值g和每两个全局矢量之间的距离d。⑥ 计算每个粒子个体极值之间的距离 dp[i]。⑦ 对每个粒子计算更新速度Vi和位置Xi时所用的个体极值P[i],如果dp[i] 式中,w为惯性因子,c1和c2是学习因子,rand( )和Rand( )是介于(0,1)之间的随机数。更新后检验每个新粒子是否在可行域内,若不在可行域内,则重更新,直到在可行域内为止。⑨设置循环迭代次数。若达到该次数,结束;否则回②。 主动齿轮的转速n1=960r/min;被动齿轮的转速n2=320r/min;传递的功率P=500kW;选用齿轮油HL-30润滑,其运动粘度v100=30mm2/s;油池温度θoil=50℃;两轮齿面粗糙度分别为Ra1= Ra2= 1.6 μm。 选取7个设计变量 式中,m——模数;Z1——主动轮齿数;b——齿轮宽度;α ——工作齿面压力角;x1,x2——分别为主动轮和被动轮的变位系数;ha*——齿顶高系数。 建立 3个目标函数:① 将基频谐波的幅值ka1最大(即f1(X)=1/ka1最小)作为追求的一个目标;② 将最小油膜厚度 hmin(X)最大(即f2(X)=1/hmin(X)最小)作为同时追求的第2个目标;③将齿轮传动总体积最小作为追求的第3个目标(其中:d1,d2分别为两齿轮的分度圆直径)。 文献[11,16]和工程经验确定下列约束条件:齿面接触疲劳强度条件、齿根弯曲疲劳强度条件、保证必要的齿顶厚、膜厚比(齿间最小油膜厚度与两齿面综合表面粗糙度之比)、限定设计变量的上下界。 按照前述的算法流程,用Matlab编制优化程序,选定粒子群数目N=100,运行次数为200,得非劣最优目标域如图2所示。根据程序运行结果,从中选取3个目标函数都接近最小值,综合性能最佳的一组结果(决策者也可根据自己的意愿选择其他的结果)作为最终方案 轮齿啮合综合刚度谱图中基频谐波幅值ka1=18.182N/(mm·μm), 齿间最小油膜厚度hmin=8.900×10-3mm,膜厚比λ=5.2018,总体积V=1.1604m3。 图2 非劣最优目标域 优化过程及结果表明,采用较多的齿数,在小于1的范围内采用较大的正变位系数,适度采用较大的压力角可以增大轮齿啮合综合刚度谱图中基频谐波的幅值,能有效地提高齿轮系统抵抗内部激励振动的能力及性价比。同时较大的压力角可以减小齿廓的曲率,变位系数的增大将增加齿廓当量曲率半径和齿面平均速度,二者都会使Hertz压力减小,齿间最小油膜厚度增加。齿顶高系数对啮合时变刚度不产生影响,当压力角较小时,它对齿间最小油膜厚度的影响不大,当压力角较大时却有明显的影响。 本文将粒子群约束多目标优化方法应用于齿轮传动系统3目标的优化设计,进行了成功地尝试,优化设计出的齿轮传动即具有较强的抵抗内部激励振动的能力及承载能力,又具有较低的产品成本。该方法进一步拓展了多目标粒子群优化算法的应用领域,能够提升齿轮传动系统的综合经济技术指标,比传统的多目标优化设计方法及通过每一单目标进行优化的现代方法具有明显的科学合理性。该方法对于其他复杂机械传动系统的约束多目标优化研究也具有一定的参考价值。 [1] 李润方,王建军. 齿轮系统动力学[M]. 北京: 科学出版社,1997: 18-26. [2] Kahraman A. Natural modes of planetary gear trains[J]. Journal of Sound and Vibration,1994,173(1):125-130. [3] Kahraman A. Planetary gear trains dynamics [J].ASME Journal of Mechanical Design,1994,116:713-720. [4] Parker R G,Agashe V,Vijayakar S M. Dynamic response of a planetary gear system using a finite element/contact mechanics model [J]. Transactions of the ASME Journal of Mechanical Design,2000,122:304-310. [5] 孙 涛,沈允文,孙智民,等. 行星齿轮传动非线性动力学模型与方程[J]. 机械工程学报,2002,38(3):6-10. [6] 秦大同,邢子坤,王建宏. 基于动力学和可靠性的风力发电齿轮传动系统参数优化设计[J]. 机械工程学报,2008,44(7): 24-31. [7] 龚小平,崔利杰,李玉超. 基于最小油膜厚度的齿轮胶合强度模糊可靠度仿真[J]. 机械设计,2008,25(10): 22-24. [8] 钱学毅,吴 双. 基于弹流润滑理论的非对称齿轮胶合强度多目标优化[J]. 工程设计学报,2010,17(6):426-434. [9] Houjoh H,Umezawa K,Masumura S. Vibration analysis for a pair of helical gears mounted on elastic shafts [C]//Proc. 7thASME Int. Power Trans and Gearing Conference,San Diego,1996: 509-518. [10] 温诗铸,杨沛然. 弹性流体动力润滑[M].北京: 清华大学出版社,1992: 122-127. [11] 肖望强,李 威,韩建友,等. 非对称齿廓齿轮弯曲疲劳强度理论分析与试验[J]. 机械工程学报,2008,44(10): 44-50. [12] Kennedy J,Eberhart R. Particle swarm optimization [C]//IEEE Service Enter,Piscataway,N.J: IEEE International Conference on Neural Networks (Perth,Australia),Piscataway,1995: 1942-1948. [13] Eberhart R,Kennedy J. A new optimizer using particle swarm theory [C]//IEEE Service Center,Piscataway,NJ: Roc. Sixth International Symposium on Micro Machine and Human Science (Nagoya,Japan),1995: 39-43. [14] 张利彪,周春光,马 铭,等. 基于粒子群算法求解多目标优化问题[J]. 计算机研究与发展,2004,41(7): 1287-1290. [15] 张 敏. 约束优化和多目标优化的进化算法研究[D].合肥: 中国科学技术大学计算机科学与技术学院,2008. [16] 肖望强,李 威,韩建友,等. 双压力角非对称齿轮传动接触分析[J]. 北京科技大学学报,2006,28(12): 1167-1173.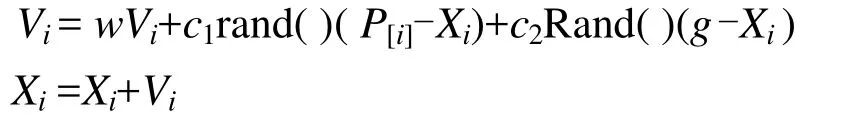
4 范 例
4.1 已知数据
4.2 选取设计变量
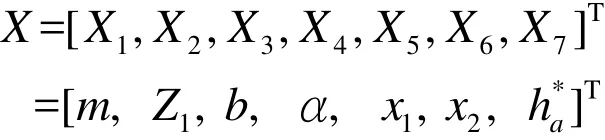
4.3 建立目标函数
4.4 确定约束条件
4.5 程序设计及结果遴选
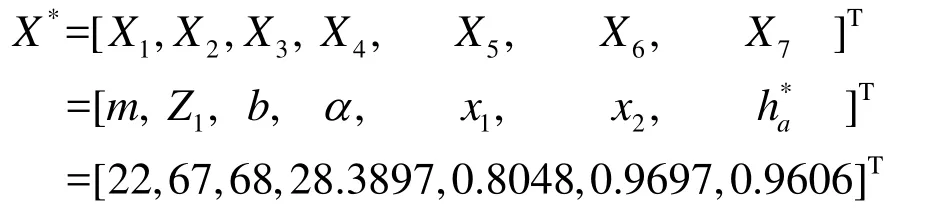
5 结 论
