多彩色空间相关分析的人脸识别算法

朱 杰 ， 陈长伟， 杨万扣， 唐振民

（1. 南京理工大学计算机科学技术学院，江苏 南京 210094；2. 东南大学自动化学院，江苏 南京 210096；3. 南京晓庄学院数学与信息技术学院，江苏 南京 211171）

人脸识别是一种理想的，重要的，具有最小侵入性的生物识别技术，其在身份认证，安全验证系统，罪犯查询，海关，重要场所进出口等领域发挥着重要的作用。近年来，人脸识别方面的研究取得很大进展，受到学术界的广泛关注。颜色是彩色图像中的重要信息，随着多媒体技术和图像采集设备的发展，颜色信息在图像处理中得到了广泛应用。几十年来，人们对彩色信息的研究是通过分别处理每一个颜色空间来达到的，未能利用各彩色空间之间的相关性，本文对此提出了新的算法。

近年来，随着小波理论的日趋成熟以及小波分析自身所具备的时频局部分析特性，小波变换在数值计算和信号处理等诸多领域得到了广泛而成功的应用。而视觉心理和生理试验表明：图像的小波变换分解过程与人类视觉系统分层次理解的特点非常类似，因此小波变换在图像压缩，图像去噪等领域获得了良好的效果。常用的变换主要有离散余弦变换（DCT）、离散傅里叶变换（DFT）和离散小波变换（DWTs）等。小波变换因对含“点奇异”的一维信号能达到“最优”的非线性逼近阶，同时又对图像具有很好的分频效果而受到重视，它把图像分成不同尺度的低频和高频图像，并成功地用于人脸识别的降维和图像的多分辨率特征表示[1-5]。Sellahewa和Jassim[6-7]已经指出低分辨率近似子带在控制的光照条件下是一种合适的人脸描述工具，但是极易受到光照变化的影响。另一方面，细节子带在变化的光照条件下仍然很稳健，但易受几何形状，如变化的人脸表情和人脸姿态的影响。Jassim和 Sellahewa[8]采用决策级融合的方法结合低分辨率和高分辨率的子带进行人脸识别，虽然取得了一定的成果，但是对于参数的选择仍然没有具体的理论基础。孙权森利用Daubechies正交小波变换进行手写数字识别和人脸图像识别也取得了较好的效果[9]。但是正交小波变换不具备移不变性，它虽然可以很好地检测图像边缘上的间断点，但是不能看到这些间断点的连续性，另外小波变换只能抓住有限的方向信息，从而对具有更多方向性的几何奇异特征表示不稀疏。所以，对于二维图像，由于边缘、轮廓和纹理等具有高维奇异性的几何特征，包含了大部分信息，小波变换不能充分利用这些几何特征，它不再是表示图像的最优或者说是“最稀疏”的基函数。为了克服小波变换的不足，M.N.Do和M.Vetterli在2002年提出了一种“真正”二维图像表示方法：Contourlet变换[10]，该变换不仅具有小波变换的多分辨率和时频局部性，而且提供了高水平的方向性和各向异性，从而可以有效地表示图像的轮廓和纹理[11-13]，在图像处理方面具有很强的优势。因此本文采用Contourlet变换得到不同分辨率下的图像特征表示。

典型相关分析(Canonical Correlation Analysis,CCA)是分析两组随机变量之间相关性的一种统计分析方法，由Hotelling[14]于1936年首先提出。其目的是寻找两组随机变量各自的线性组合，使得线性组合后的两个随机变量的相关性达到最大[15]。近几十年来，CCA在众多领域得到了广泛的应用，诸如信号处理[16-17]，医学研究[18]以及人脸识别[19-20]等领域。在图像识别等应用中，当图像样本个数小于样本维数时，CCA方法要面临协方差矩阵奇异所导致的小样本问题(Small Sample Size,SSS)。针对这个问题，我们采用PCA[21]统计方法将图像的零空间先行丢弃，再使用CCA方法进行特征选取。孙权森等[9]将典型相关分析用于特征层的融合成功地解决了手写图像识别问题。我们采用CCA方法求取不同分辨率观测空间的相关子空间，然后把观测空间的向量分别投影到相关子空间，最终在相关子空间中进行特征融合和分类。

本方法应用于彩色AR人脸数据库来进行人脸识别实验。结果表明，该方法不仅优于单个分辨率图像的识别结果，而且在时间效率方面也具有良好的性能。

1 多空间彩色人脸识别方法

1.1 Contourlet变换及特性

Contourlet变换是一种新的多分辨率，局域的，多方向的，“真正的”图像稀疏表示方法，仅用少量系数就能有效地表示在图像中体现重要特征的平滑轮廓。它是2002年Mich N.Do和Martin Vetterli在Curvelet变换的基础上，结合方向滤波的思想提出来的。

Contourlet变换首先是在离散数字域中提出的，随后才推广到连续域中加以分析。它类似于小波基从滤波器组导出的方式，采用了不可分的滤波器组构造离散域上多分辨率的，多方向的基函数。基的支撑区间是具有随尺度变化长宽比变化的“长条形”结构，类似于轮廓段，具有方向性和各向异性的尺度关系，能有效地表示图像。Contourlet变换使用两个滤波器组，其中前一个拉普拉斯塔形分解（Laplacian Pyramid，LP）滤波器组用来捕捉点奇异，每一层次拉普拉斯金字塔分解产生一个下采样的低通部分和一个该图像与预测图像的差图像。接下来的方向滤波器组DFB（Directional Filter Bank）用以将奇异点连结成线结构，这种结构使得Conoutlet具有较优的非线性逼近性能，它可以很好的按方向分解图像并具有很好的重构性。因此Contourlet变换也称为金字塔型方向滤波器组PDFB（Pyramidal Directional Filter Bank）。

Contourlet变换有效地表示了轮廓和纹理丰富的图像。因为它是将金字塔分解和方向滤波器结合起来实现的。每一级Contourlet分解都会产生一个低频分量和一系列的高频子带，然后在该尺度的低频子带中继续分解，是一个不断迭代处理的过程。单独使用任何一部分都不能很好地描述图像。金字塔分解不具有方向性，而方向滤波器对高频部分能很好分解，对低频部分不行，二者的结合恰好相互弥补不足，因此可以很好的描述图像。Contourlet子带系数的分布具有非线性相关性，它是基于多分辨率分析的算法，能够较好地表示图像信息。低频系数反映图像的轮廓信息，对应图像频率的“慢变”部分，故系数间的相关性高；高频系数反映图像的细节信息，对应图像频率的“快变”部分，故系数间的相关性低。我们采用低频图像和高频图像的平均和，提取其最大相关性，从而可以得到理想的基函数。

1.2 CCA相关分析

CCA的方法源于研究两组随机向量之间的相关性的问题，是利用综合变量对之间的相关关系来反映两组指标之间的整体相关性的多元统计分析方法。其目的是寻找一组变量的线性组合与另一组变量的线性组合，使两者之间的相关达到最大。假设两类样本，其中D表示样本的维数，m，n分别表示X和Y的样本数。要寻求一对线性变换wx，wy，使得：X在wx上的投影为Z1=Xwx，Y在wy上的投影为Z2=Ywy，并使得两组向量投影后的相关性最大，即

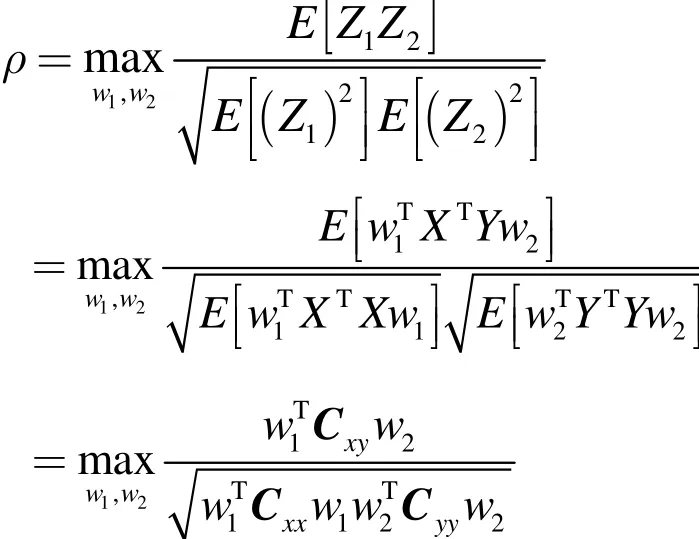
其中，Cxx，Cyy分别表示数据X，Y的协方差矩阵；Cxy表示数据X和Y的协方差矩阵。

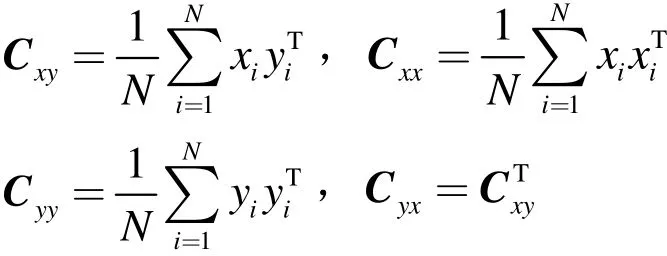
根据典型相关分析的思想，向量间的相关度达到最大，即满足约束条件时，转化为求的最优化的求解问题。通过拉格朗日乘子法，于是以上方程的求解可转化为解方程的广义特征值和广义特征向量

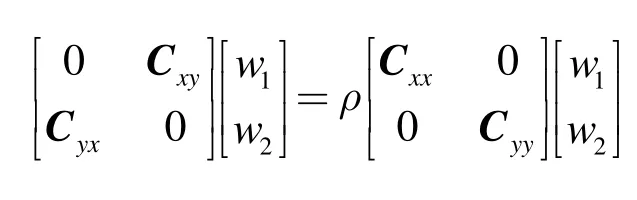
对上式进行广义特征值分解，求得典型相关系数ρ和最佳典型投影向量 W =[w1,w2]。

1.3 本文方法

首先提取5个不同色彩空间（RGB,YCbCr,HSV,YIQ,YUV）的不同通道（如R,G,B三通道，H,S,V三通道，YUV三通道等）的信息，然后取每个空间的3个通道信息的平均和，如RGB三通道中RGB的平均信息和，YUV三通道YUV的平均信息和等。得到不同通道信息和之后，采用Contourlet小波变换，分别得到不同色彩空间的高频和低频信息，低频信息直接得到，高频信息用不同分辨率的高频信息平均和得到。对得到的高低频信息用PCA进行降维，然后对高频信息和低频信息进行CCA相关性分析，使得不同频率信息得到最充分利用，求出投影系数，对数据进行投影变换后进行决策级融合的最近邻分类，最后得到识别结果和运行时间，具体步骤如图1所示。解，也使用分解后的低频分量和高频分量作为新的数据集进行实验，如表1所示。为了计算方便，我们先采用PCA对数据进行降维，我们分别用维数10，20，30，到100共10个维数进行实验。

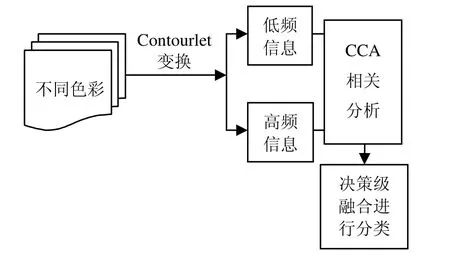
图1 本文方法流程图

用cca对降维后的数据进行相关分析，得到投影变量，把测试数据经过投影后，用决策级融合的最近邻分析法进行识别，采用cos距离进行测量。

2 实验与分析

2.1 彩色AR人脸数据库简介

为了验证彩色图像的Contourlet变换技术以及典型相关分析及决策级融合算法的可行性和优越性，所采用的实验基于彩色AR人脸数据库。彩色AR人脸数据库包含120人，每人26副图像。图像中人的脸部表情和姿态有着一定程度的变化，并存在戴着围巾的图片，在年龄，姿态，发型，光照和装扮等方面都有不同程度的变化，因此在彩色AR图像库上进行的实验具有一定的通用性。在进行实验前，通过瞳孔，鼻子和嘴巴坐标，对人脸图像进行预处理。试验中，为了方便计算，图像大小归一化为50*40。图2给出了库中的部分图像。

图2 彩色AR人脸数据库

2.2 实验结果及其分析

我们选择了10幅图片进行实验，训练样本数分别采用4，5，6，7，8；总的类别数为120。首先是采用不同的色彩空间对算法的影响实验。I1空间为RGB空间，I2空间为YCbCr空间，I3空间为HSV空间，I4空间为YIQ空间，I5空间为YUV空间。对每个彩色空间进行contourlet分解，分别取 Contourlet分解后的低频分量和高频分量作为新的数据集；为了比较我们提出方法的有效性，我们同样对每个彩色空间进行Daubiechies分

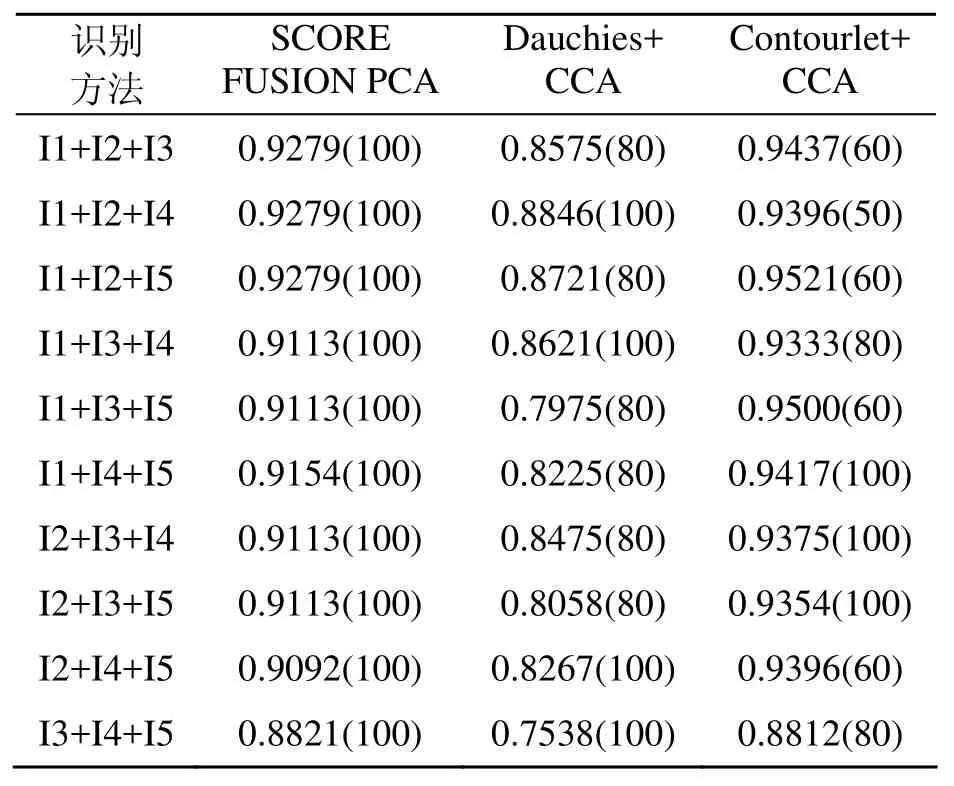
表1 不同色彩空间的cca算法（识别率训练数为6，括号中是识别率最大时的维数）

分析实验结果可以发现，RGB，YCbCr和YUV 3个彩色空间进行CCA变换后再决策级进行融合得到的识别率最高；而HSV，YIQ和YUV 3个彩色空间进行 CCA变换后再决策级融合得到的识别率较差。在 YCbCr格式中，亮度信息用单个分量Y来表示，彩色信息用两个色差分量Cb,Cr来表示。Cb分量是蓝色分量和一个参考值的差，Cr分量是红色分量和一个参考值的差。YUV模型中，Y表示亮度信号，U，V表示色差信号，UV构成彩色的两个分量，YUV的亮度信号Y和色度信号U，V是相互独立的。因此RGB空间和 YCbCr及 YUV空间中的色彩信息相关联，YCbCr和YUV中的亮度信息相关联，三者相关性达到最大后识别效果也最好。对于 HSV颜色空间，V 分量（亮度）与彩色信息无关；H分量（色调）和S分量（饱和度）与人感受彩色的方式相关。YIQ模型，其中Y表示亮度，I，Q是两个彩色分量，他们之间仅通过不同方式的亮度信息相关联，因此识别效果较差。

为了得到更可靠的实验结果，本文对不同的训练数目进行了大量的实验，分别对于 4个，5个，6个，7个和8个训练数目做了实验，每种结果取其最佳识别率。实验结果如图3所示。

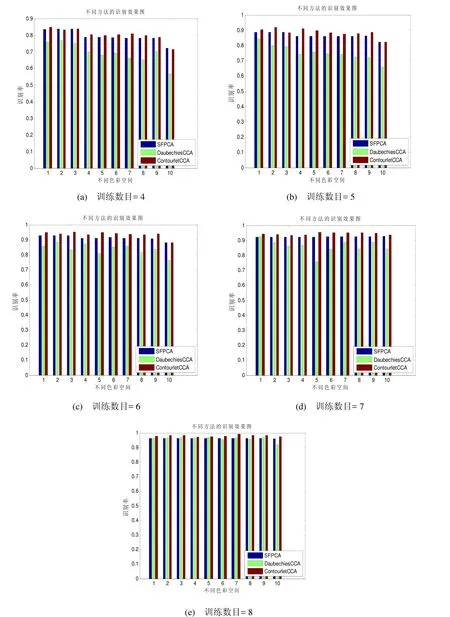
图3 10个不同的色彩空间在不同训练数下的识别率

Contourlet+CCA方法的识别率最高，SFPCA次之，Daubechies+CCA在训练数目较少的时候效果不好，随着训练数目的提高，其识别率超过了SFPCA，但仍然低于Contourlet+CCA方法。这是由于训练数目增多，能更好地表示数据之间的相关关系，所以随着训练数增多，Daubechies的效果得到了显著提高，Contourlet+CCA同理。

最后，我们比较一下几个实验的运行时间（指从10维到 100维共10次运算后的平均时间），如表2所示。可以看出，本文提出的方法不仅识别能力明显优于其他算法之外，在运行效率方面也表现出优越性。

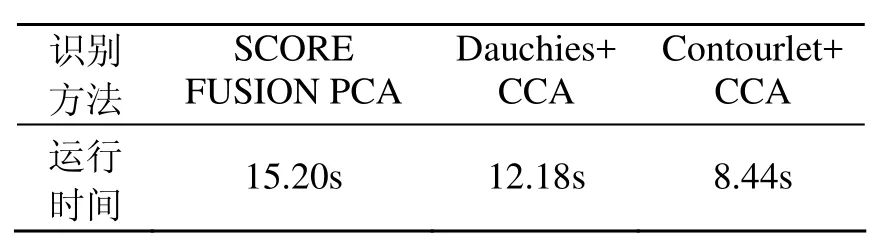
表2 不同算法的运行效率（训练数为6）

3 结 论

本文提出一种基于 Contourlet分解和典型相关分析方法的彩色人脸识别算法。算法使用Contourlet变换对脸部信息进行了预处理，降低了数据量，提高了运行速度；接着使用典型相关分析的相关度最大方法使数据不同频率的信息得到充分利用，找到了最合适的投影基。对彩色 AR人脸数据库德识别实验结果表明，本文方法优于孙提出的Daubiches+CCA方法和传统的PCA算法，改进的算法识别率最高可以达到99%的识别率，而且在运行时间效率方面也有很强的优势。

本文图像的特征提取是基于二维图像的一些二维的处理和变换，今后的工作中可以考虑多方位的二维图像获取三维特征，以提高对个体人脸表情，光照的鲁棒性。在今后的试验中将会在更多的库中进行试验，以提高系统的推广性。

[1] Manjunath B S,Chellappa R,Malsburg C. A feature based approach to face recognition [C]//Proceedings CVPR ’92. 1992 IEEE Computer Society Conference on Computer Vision and Pattern Recognition,1992:373-378.

[2] Lai Jianhuang,Yuen P C,Feng Guocan. Face recognition using holistic fourier invariant features [J].Pattern Recognition,2001,34(1): 95-109.

[3] Chien J T,Wu C C. Discriminate wavelet faces and nearest feature classifiers for face recognition [J].IEEE Trans. Pattern Anal. Mach. Intell.,2002,24(12):1644-1649.

[4] Sellahewa H,Jassim S. Wavelet-based face verification for constrained platforms [C]//Proc. SPIE Biometric Technol. Human Identification II,Mar,2005,5779:173-183.

[5] Ekenel H K,Sankur B. Multiresolution face recognition [J]. Image Vis. Comput.,2005,23(5):469-477.

[6] Sellahewa H. Wavelet-based automatic face recognition for constrained devices [D]. Ph.D.dissertation,Univ. Buckingham,Buckingham,U.K.2006.

[7] Sellahewa H,Jassim S A. Illumination and expression invariant face recognition: toward sample quality-based adaptive fusion [C]//Proc. 2nd IEEE Int.Conf. Biometrics,2008: 1-6.

[8] Jassim S A,Sellahewa H. Multi-stream face recognition on dedicated mobile devices for crime-fighting [C]//Proc. SPIE Opt. Photon.Counterterrorism Crime Fighting II Sep.,2006,(6402):1-10.

[9] Sun Quansen,Zeng Shenggen,Liu Yan,et al. A new method of feature fusion and its application in image recognition [J]. Pattern Recognition,2005,38:2437-2448.

[10] Do M N,Vetterli M. Contourlets [C]//Beyond Wavelets,J. Stoeckler and G.V. Welland,Eds.Academic Press,New York,2002: 1-27.

[11] Yu S J. Direct blind channel equalization via the programmable canonical correlation analysis [J].Signal Processing,2001,81: 1715-1724.

[12] Borga M. Canonical correlation：a tutorial [EB/OL].(2001).http:// www. imt. liu. Se / ～magnus/cca/2001.

[13] Borga M. Learning multi-dimensional signal processing [D]. Linkping University,Sweden,1998.

[14] Hotelling H. Relations between two sets of variants [J].Biometrika,1936,28: 321-377.

[15] Becker S. Mutual information maximization：models of cortical self organization [J]. Network:Computation in Neural Systems,1996,7(1): 7-31.

[16] Do M N,Vetterli M. Contourlets: a directional multiresolution image representation [C]//IEEE International Conference on Image Processing.Rochester,NY: IEEE,2002: 357-360.

[17] Do M N,Vetterli M. The contourlet transform: an efficient directional multiresolution image representation [J]. IEEE Transactions on Image Processing,2005,14(12): 2091-2106.

[18] Do M N. Directional multiresolution image representations [D]. Ph.D. Thesis,Department of Communication Systems,Swiss Federal Institute of Technology Lausanne,2001.

[19] Melzer T,Reiter M,Bischof H. Appearance models based on kernel canonical correlation analysis [J].Pattern Recognition,2003,36: 1961-1971.

[20] Zheng Wenming,Zhou Xiaoyan,Zou Cairong,et al.Facial expression recognition using kernel canonical correlation analysis (KCCA) [J]. IEEE Trans on Neural Networks,2006,17(1): 233-238.

[21] Turk M,Pentland A. Eigenfaces for recognition [J]. J.Cognitive Neuroscience,1991,13(1): 71-86.

[22] Yu Xuelian,Wang Xuegang,Liu Benyong. Supervised kernel neighborhood preserving projection for radar target recognition [J]. Signal Processing,2008,88(9):2335-2339.

[23] Ye Guiyun,Liu Changzheng. Image compression based on fast lifting wavelet transform [J].Networking and Digital Society,2009,(1): 261- 264.