基于黎曼度量参数曲面四边形网格生成方法及UG实现

郭新强， 张见明， 覃先云， 穆东辉， 宋 乔

（1. 湖南大学汽车车身先进设计制造国家重点实验室，湖南 长沙 410082；2. 北京第二机床厂有限公司，北京 100072）

曲面网格生成的方法通常分为直接法和映射法[1]。直接法是指曲面网格的划分直接在曲面的物理空间进行；映射法是首先利用平面域网格生成方法在曲面的二维参数空间进行网格剖分，然后将剖分结果映射到三维物理空间形成曲面网格。本文利用反映曲面扭曲程度的黎曼度量[2-4]，将用于生成平面四边形网格技术的铺砖法[5]扩展运用于任意复杂曲面的网格生成。铺砖法首先由Blacker T D和 Stephenson M B提出的，该法具有较高的边界灵敏度，可以较好的拟合网格区域复杂的边界形状，能生成质量较高的网格。在原有的铺砖法中，首先沿着网格边界生成一排单元，然后再考虑相交情况，使得相交处理复杂。在本文实现该方法过程中，每生成一个单元时就预先判断相交情况，根据判断对相交单元做简单的处理，省去了原方法中对多次相交优先处理环节，从而使得整个的相交处理变得简单。

本文利用改进的铺砖法生成的四边形单元是用于一种新的结构分析算法——边界面法[6]前处理的二维参数曲面网格。边界面法由张见明等人最近提出，该法直接利用CAD实体模型的边界参数曲面信息在二维参数空间中划分网格并在曲面的二维参数空间内进行边界积分和变量插值。在数值积分过程中，积分点的几何数据直接由参数曲面的参数变量计算得到[7]，而不是基于单元由多项式插值近似的，避免了几何误差。该方法中所使用的四边形单元定义在曲面的二维参数空间，而不是像有限元法中的单元定义在三维物理空间。有限元法的几何模型是通过单元插值近似的，当网格较稀疏时具有明显的几何误差。边界面法是利用二维参数空间的值进行数值计算，现有的有限元前处理商业软件能输出模型的三维物理空间坐标，但必须再经过计算才能获得二维参数空间的值。因此，该类单元不能从现有的有限元法前处理的商业软件中直接得到。为了保证良好的积分和插值精度，一般要求二维参数单元在对应的三维物理空间中的网格具有良好的形状。为此，作者将铺砖法运用到任意复杂曲面生成参数曲面网格，实现边界面法的前处理。

UG是一款采用全参数化建模CAD软件，并提供了强大的二次开发工具UG/Open[8]。本文通过VC++编程调用UG/Open库函数获取CAD模型的曲面参数信息。在参数域内利用改进的铺砖法生成网格，然后将二维参数域上生成的网格映射到曲面的三维物理空间，从而生成曲面的最终网格。为了使二维参数域上生成的网格投到曲面的三维物理空间保持较好的质量，本文在参数域上生成网格时运用黎曼度量方法对网格的形状和大小进行控制。文章最后给出了4个算例验证了算法的可靠性，并且说明了不论是在平面还是曲面上都能生成质量较好的四边形网格。

1 黎曼度量

曲面二维参数域上的点与三维物理空间的点是一一对应的关系。对于简单的曲面直接映射法能生成质量较高的网格，对于曲率变化剧烈的曲面，由于其映射函数在参数域的两个方向的非线性生成的网格的质量往往较差。为了使二维参数域上生成的网格投影到曲面的三维物理空间保持较好的质量，采用黎曼度量的方法可以控制网格形状和大小。

1.1 参数曲面的黎曼度量

三维空间的一个参数曲面S与二维参数空间的一一对应关系可用函数表示为

在UG二次开发环境中，只需知道二维参数域中每个节点u和v两个参数值就可以调用的库函数UF_MODL_evaluate_face（…）获得节点沿参数u和v的切向量Su和Sv，进而得到参数曲面黎曼度量矩阵。

1.2 参数线段弧长计算

参数域内线段两端点为 P1和 P2，则该线段上任意点可表示为 P = P1+ ( P2- P1)⋅ t ，0≤t≤1。P点的黎曼度量可表示为

考虑黎曼度量后线段上两点A和B的在三维物理空间长度可以用下面公式计算[2]

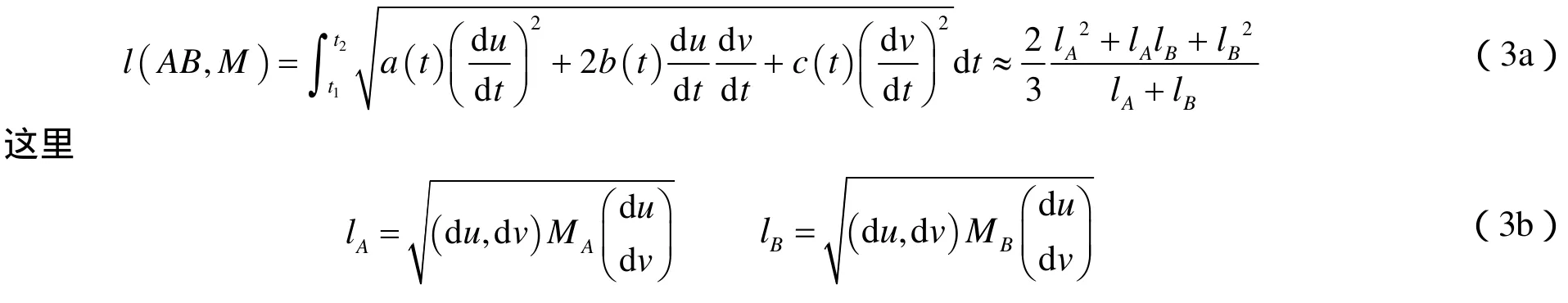
当曲线上两点A( t1)，B( t2)的度量矩阵特征值变化不大时可用上式，否则需要把线段分成若干段，计算每小段li的长度，总长度为

1.3 参数向量的旋转

二维参数空间中向量AB需逆时针旋转一个角度后得到新的向量AC，则向量AC由下式计算得到[3-4]

lAB为向量AB在三维物理空间的长度，可根据参数弧长计算公式(3a)或者式(3c)得到，lideal为生成C点所需的三维物理空间理想长度，φ根据前沿DA和AB映射到三维物理空间中形成的角度∠DAB而确定。如图1(a)图1(b)，沿AB逆时针方AB逆时针方向φ为的度量矩阵，根据公式(4)即可求出向量AC，点A为已知点，则可以求出C点在二维参数空间的值。

图1 向量旋转角度

2 曲面参数空间四边形生成

2.1 网格生成过程

根据铺砖法的一般原理，如图2给出了生成曲面网格的整个流程。本文对相交处理做了改进，并且在2.2做了详细的阐述，其它过程只简单介绍，其细节可以参考文献[5, 9-10]。

1）边界离散

调用UG库函数获得实体表面的参数域，对参数域的边界进行离散。内边界点按顺时针方向连接，外边界点按逆时针方向，且保证离散点数为偶数。

2）节点分类及最优边选择

节点内角是指节点Ni与其所在边界上前一节点Ni-1和后一节点Ni+1投到三维物理空间的角度。根据节点内角的不同分为 4种类型：(1) 终 止 节 点 α≤ 1 35°；(2) 边 节 点135°＜ α ≤ 2 25°；(3) 角节点225° ＜ α ≤ 3 00°；(4)转节点300° ＜ α ≤ 3 60°。

如果Ni为终止节点则边界 NiNi+1为最优边开始生成单元，每次选取前沿边界中的一条边作为基边生成四边形。

3）生成新单元及相交判断

本文中单元是在二维参数域中生成的。每次生成一个新的单元是根据基边两个端点的节点内角在参数域中生成新的节点，从而生成新的单元。新节点的位置可根据公式(4)确定，其中 lAB为基边在三维域中长度，lideal的长度可以参考文献[5, 9-10]中计算新节点的向量长度，MA是节点的度量矩阵。形成单元后，新边要判断是否与前沿边界相交，如果相交就进行处理，在下节中详细介绍相交处理过程。

4）生成一排单元及边界调整

以终止节点作为新生单元的起点，如果没有终止节点选择最小节点内角作为起点，直到再次遇到终止节点完成一排单元的生成，当所有的活动前沿边界都作为基边生成单元后就完成一层单元的生成，然后更新活动前沿边界。一层单元生成后，如果更新的活动前沿边界尺寸有变大或者缩小的趋势则进行单元楔入或者删除单元操作，具体过程参考文献[5, 9-10]。

5）光滑处理和缝合处理

为了使生成的边界尺寸大小均匀，以及边的垂直度，可以对更新的前沿边界节点进行边界光滑，内部节点进行内部光滑。如果尺寸过渡比较大或者出现内角很小的情况可以进行缝合处理，详细情况可以参考文献[5, 9-10]。

6）闭合处理及优化网格

当前沿边界节点数目小于等于4时就进行封闭处理，整个区域网格生成完成。用改进的铺路法完成全四边形网格生成后，每个节点最理想的是由4个单元共用，这样形成的四边形较规则。如果每个节点由3～5个单元共用，生成的单元是符合要求的。由于几何边界的复杂性和网格尺寸不均匀常常导致局部网格形状不好，所以需进一步优化。优化后需再对除几何边界节点外节点用内部节点光滑方法进行几次迭代光滑，保证生成的网格质量更好。

图2 程序流程

2.2 相交处理

原有的铺砖法网格是逐排生成的，生成一排单元后再去处理相交问题。如果采用这种方法处理，特别是出现多次相交还要进行优先处理判断，这样使程序比较复杂。本文对相交处理过程做了改进，采用生成一个单元时就进行相交判断，如果遇到相交就进行相交处理。

经过改进后的相交处理过程可分为 3个部分：

1）优先处理新单元中相交线段新生成的点；

2）如果1）未完成处理则处理新单元中相交线段原有节点；

3）如果前两步都未处理好，则搜索基边节点附近的点，如果满足要求则替代新节点，如果没有满足要求的点则取消此单元生成，并以相邻边作为基边生成单元。

如图 3所示，新生成的单元边 NiNi+1和NiNi-1与前沿ab相交，Ni为新生成的点，相交处理后必须保证边界形成环后的节点数为偶数，图3中是两个环合并为一个环，Ni点距离b点近所以选b作为替代的点，图3(c)所示。点Ni被点b替代后根据点b两边的角度来确定边的合并，如图3(d)所示为合并边后的结果。

图3 新节点相交处理

如图4所示，图4(a)中直线未相交，此时以边NiNi-1作为基边生成四边形，生成新节点Nj并生成四边形，图4(b)图所示，新生成的单元边Ni+1Nj与前沿ab相交，如果新节点由节点a替代形成的边界环不满足偶数个节点要求，如果新节点由节点b替代生成的边还是与前沿相交，此时考虑节点 Ni+1由a或者b替代。在本例中由a替代，如图4(c)所示。缝合最终生成的图形如图4(d)所示。

图4 原节点相交处理

如果以上两个处理过程都不能生成单元，则进行第3步处理。如图5所示，边界AB为基边，根据节点B的节点内角生成C点，假设C点按前面两步都不能处理相交问题，则以B为中心在参数空间建立一个搜索区域，在区域内寻找最优的点。

首先确定在三维空间的搜索半径r3D，一般取边界AB在三维空间长度的两倍。考虑度量矩阵，以搜索半径r3D构成的区域在参数空间里为一椭圆，参数椭圆的中心在B点。因此，要计算参数椭圆的长半径和短半径，以确定简单的参数矩形。根据搜索半径r3D，由以下公式计算对应的参数半径

方程(5)等价于中心在圆点极坐标中的椭圆方程，能转化为参数坐标下椭圆形式的方程为

通过旋转椭圆与坐标轴平行，方程(6)可以简化，得到椭圆在参数空间的长短半径分别定义为

得到椭圆的长短半径后，可以简单地在参数空间里确定矩形搜索区域，如图4所示的矩形框。搜索区域建立好后选择最优点，如图6所示，前沿节点P1, P2, P3为搜索区域内的点，最优点形成四边形后要保证每个边界前沿节点数目为偶数个，图中P2不满足要求，P1和P3满足奇偶性要求，本文中选取∠APB张角最大的点，即P1是最优点。

图6 选择最优点

3 四边形质量评价因子

网格质量的好坏将影响计算精度，本文采用几何准则对四边形网格进行质量评价。如图7所示四边形ABCD的两条对角线将其分为4个三角形△ABC，△ABD，△CDB，△CDA，通过计算这4个三角形的质量因子得出该四边形的质量因子。

图7 分割四边形

三角形ABC的质量α因子[11]定义如下

n是三角形的单位法向量，α的意义就是三角形面积与变长的平方和之比，0＜α≤1，α越大三角形质量越好。令4个三角形△ABC，△ABD，△CDB，△CDA的α因子分别为1α，2α，3α，四边形β因子[12]定义为

0＜β≤1，β越大四边形质量越好，根据文献[11]中β不同的范围来评价四边形质量，如表1所示。

表1 四边形 β 评价因子[11]

4 UG实现过程

本文利用VC2005编程平台通过External连接方式实现UG二次开发。首先，在VC2005环境里建立一个动态(.dll)项目。然后，对项目进行设置即可与 UG/Open API建立连接关系。在VC2005编译环境里对VC++项目的设置为：

1）菜单选项-工具选项项目和解决方案VC++目录：

在“库文件”和“包含文件”里添加UG安装目录下的UGSNX 4.0UGOPEN

2）菜单选项-项目属性页连接器输入附加依赖项：

添 UG Open 的库文件名 libufun. lib,libugopenint. lib和libnxopencpp.lib。

3）菜单选项-项目属性页连接器常规输出文件：

添加‥startup$(ProjectName).dll。

4）菜单选项-项目属性页配置属性常规字符集：

下拉选项中选择为“使用多字节字符集”。

通过上面的设置，VC++环境里的项目与UG/Open建立了联系，成功编译项目后就在该项目目录下的startup文件中生成相应可以在UG中执行的.dll文件。在 UG环境里利用菜单工具——调用.dll就可以在相应的曲面上生成网格。

当与 UG/Open建立联系后可以调用其中的库函数获取实体模型的曲面信息，根据获得的曲面参数空间进行边界离散，并运用第2节中的网格生成方法在参数空间生成网格，并映射到三维物理空间。

下面给出在 UG/Open API中常访问和生成几何的函数以及功能：

UF_MODL_ask_body_faces(…)：获得实体的所有曲面；

UF_MODL_ask_face_edges(…)：获得曲面的所有边界曲线；

UF_MODL_ask_face_uv_minmax(…)：获得曲面的参数范围；

UF_MODL_evaluate_face（…）：获得节点沿参数u和v的切向量以及节点映射到三维物理空间的坐标；

UF_POINT_create_on_surface(…)：在曲面上生成点；

UF_CURVE_create_line(…)：生成线段；

UF_OBJ_set_color(…)：生成的网格在物理空间的颜色显示。

5 网格生成实例

该节给出了利用本文算法生成曲面四边形网格实例，如图8～图11所示。网格单元直接在UG环境中的CAD模型表面生成，保持了模型的原始几何信息。根据网格质量因子对各种实例的网格质量进行了评价，其结果如表2所示。可以看出基于黎曼度量改进后的铺砖法无论在平面还是曲率大的曲面都可以获得质量较好的网格。

图8 实例1

图9 实例2

图10 实例3

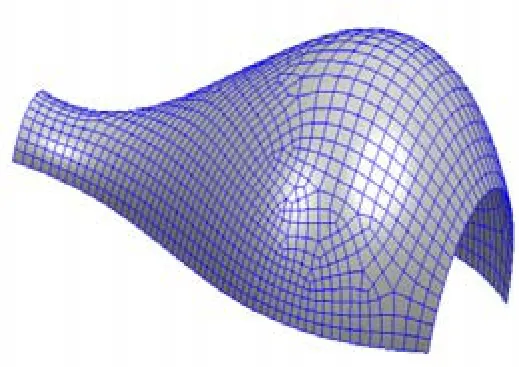
图11 实例4

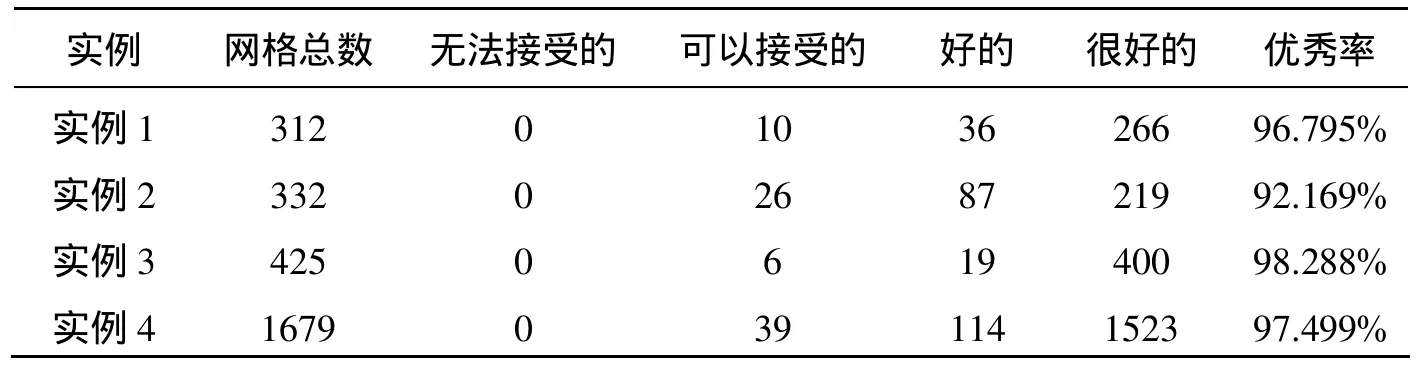
表2 实例质量评价表

6 结束语

本文基于黎曼度量将铺砖法扩展运用到任意曲面的四边形网格生成，并在原有算法的基础上对相交处理过程做了改进，使得相交处理更加简单有效。基于UG二次开发工具，利用VC2005平台在UG建模环境中实现了曲面的二维参数空间网格划分，且网格单元在三维空间质量较好。在网格生成过程中，调用UG Open/API中相应的库函数，获取CAD实体边界曲面参数信息，并将最终生成的网格显示在实体表面。后续的工作是将这种参数四边形网格应用到边界面法中作为前处理网格。边界面法与CAD无缝连接能避免几何误差，提高计算精度，实现CAD与CAE的无缝连接，对数值计算有非常重要的意义。

[1]张建华, 叶尚辉. 有限元网格自动生成典型方法及发展方向[J]. 计算机辅助设计与制造, 1996, (2):28-31.

[2]关振群, 单菊林, 顾元宪. 基于黎曼度量的复杂参数曲面有限元网格生成方法[J]. 计算机学报, 2006,29(10): 1823-1833.

[3]Lee C K. Automatic mesh generation using metric advancing front approach [J]. Engineering Computations, 1999, (16): 230-263.

[4]Lee C K. Automatic adaptive metric advancing front triangulation over curved surfaces [J]. Engineering Computations, 2000, 17: 48-74.

[5]Blacker T D, Stephenson M B. Paving: a new approach to automated quadrilateral mesh generation [J].Numer. Meth. Engrg, 1991, 32: 811-847.

[6]Zhang Jianming, Qin Xianyun, Xu Han, et al. A boundary face method for potential problems in three dimensions [J]. Numer. Meth. Engrg, 2009, 80:320-337.

[7]覃先云. 基于参数曲面的边界面法研究[D]. 长沙:湖南大学, 2009.

[8]侯永涛, 丁向阳. UG/Open 二次开发与实例精解[M].北京: 化学工业出版社, 2002: 1-2.

[9]张清萍, 尚 勇, 赵国群. 二维全四边形网格的自动生成算法[J]. 山东大学学报, 2002, 32(3):254-259.

[10]林胜良, 方 兴, 张 武, 等. 一种改进的高品质全四边形网格生成方法[J]. 江南大学学报, 2006,5(1): 70-73.

[11]Lee C K, Lo S H. A new scheme for the generation of a graded quadrilateral mesh [J]. Computers and Structures, 1994, 52: 847-857.