基于Q学习的任务调度问题的改进研究

刘晓平， 杜 琳， 石 慧

（合肥工业大学计算机与信息学院，安徽 合肥 230009）

随着产品设计的复杂化和多样化，协同工作已成为设计制造领域中的必由之路。协同工作的开展，不仅加强了企业内部和企业间的交流与合作，更能够充分发挥企业自身的群组优势，从而提高产品的开发效率，增强企业在市场中的竞争力。而在产品生产过程中，任务的规划和分解，子任务间的调度与优化作为协同工作的基础，就显得尤为重要。目前，有效的调度方法与优化技术的研究和应用，已经成为先进生产技术实践的基础和关键，所以对它的研究与应用具有重要的理论和实用价值[1]。

任务调度问题已经被证明是一个NP完全问题[2]，不可能在多项式时间内找到问题的最优解。近年出现的一些启发式算法为求解此类NP完全问题提供了新的途径。其中，遗传算法以解决大空间、非线性、全局寻优等复杂问题时具有传统方法所不具备的优越性，受到了研究人员的普遍关注[3-5]。但是，遗传算法在求解大规模任务调度问题时存在的计算效率偏低、收敛于局部最优解等弊端，也不容忽视，因此有必要寻求更加有效的算法来解决此问题。强化学习作为一种无监督的学习方法，它具有其他机器学习方法无可比拟的优点，它考虑的是在没有外界指导的情况下，智能体通过与不确定的外界环境进行交互，从而获得最优解的学习过程。Wei Yingzi等人将Q学习应用于动态车间作业调度中，取得了较好的效果[6]。Shah等人在无线传感网络中，提出了一种基于Q学习的分布式自主资源管理框架，并通过仿真与对比试验，证明其比现存的其他方法大大提高了系统效率，并且提出了一种基于多步信息更新值函数的多步Q学习调度算法，并结合实例阐明其解决任务调度问题的有效性[7]。针对此，本文改进了现有的基于Metropolis原则的Q学习算法，并将其应用到协同设计的任务调度上，通过和文献[8]所示实例的对比，表明该算法具有更好的收敛速度和泛化性。

1 问题定义

任务调度问题可以简单的描述为，由设计任务分解出的N个子任务要在M个处理机上加工，每个子任务要在某个处理机上连续加工一段时间，调度就是将各个子任务恰当的分配给处理机，使给定的目标得到最优解。

下面，作者给出任务分配和调度问题的一般性定义：

4）一个任务约束关系图，由任务前驱图[9]来表示各个子任务间的时序约束关系，如图1是7个子任务的约束关系图。对于一个任务前驱图G，G=(T，L)，其中T为子任务集，一个子任务Ti，就是图G中的一个节点；L是任务前驱图中的有向边集，它表示任务之间的直接驱动关系，(Ti，Tj)∈L即子任务 Tj必须在子任务 Ti完成之后才能执行，Ti为 Tj的一个前趋，Tj为 Ti的一个后驱。

图1 任务前驱图

5） 子任务节点Ti的深度值

（2）调度在同一台处理机中的所有任务是按深度值升序排列的。

现在的目标就是，寻找一个分配调度策略s，将n个子任务指派到m个处理机上，合理调度各个子任务的执行顺序，使得各个任务在满足任务前驱图G的约束下，整个大任务的完成时间t(s)最短。

2 算法描述

2.1 任务调度的MDP模型

强化学习以马尔可夫决策过程(Markov decision process, MDP)为基础[10]，通过试错机制来获得最优行为策略。因此，采用强化学习求解设计任务调度问题的关键就在于如何将调度问题建模为MDP 模型。一个MDP模型可以表示如下其中S为状态空间，A为动作空间，系统处于状态St时，执行决策动作at后转移到下一状态的转移概率，r( St, at)为在状态St下执行动作at获得的立即回报， W ( St, at)为值函数。MDP的本质是：当前状态向下一状态转移的概率和回报值只取决于当前状态和决策，而与历史状态和决策无关。据此，本文给出如下MDP描述

1）状态空间S由任务匹配矩阵TPm×n表示，即任务调度问题的一个可行解。强化学习的状态转移就是在解空间上的搜索。

2）动作空间A由子任务的集合T表示，对于任一状态，都有n个动作，也即n个任务数。第j个动作（1≤j≤n）把第j个任务迁移到下一个处理机中，如果当前状态中dij= 1，那么动作i

3）由上可知转移概率p(St,at,St+1)=1。

2.2 Q学习

Q 学习是一种基于随机动态过程的不依赖模型的强化学习方法。自Watkins等[11]提出Q学习并证明其收敛性以后，该算法在强化学习研究领域中得到了人们的普遍关注。Q学习过程由步骤(step)和情节(Episode)组成，每个情节包含若干步骤。Q学习在训练过程中，不断重复以下步骤：观察当前状态St，选择和执行动作at，转变为下一状态St+1并接受即时回报 r ( St, at)，然后利用下式来调整Wt值

其中，学习率0 ≤ η ≤ 1控制学习的速度，学习率越大，收敛越快，但容易产生振荡；学习率越小，收敛越慢。折扣因子0≤γ≤1表示学习系统的远视程度，如果取值比较小，则表示系统更关注最近的动作的影响；如果比较大，则对比较长的时间内的动作都很关注。一般来说，η取得较小，γ取得较大[10]。

2.3 Metropolis规则

模拟退火(Simulated Annealing, SA)算法近年来被证明是解决组合优化问题的有效近似算法，其基本思想就是用一个物理系统的退火过程来模拟优化问题的寻优过程，当物理系统达到最小能量状态时，优化问题的目标函数值也相应地达到其全局最优值。

模拟退火算法通过Metropolis准则来确定接收新解的概率

其中， f ( xi)为当前解， f ( xj)为新产生的解，f( x)为目标函数，T为控制参数，类似固体退火中的温度。因此，模拟退火算法并非总是接受优化解，还在一个限定范围内接受恶化解，从而有助于跳出局部最优。只要初始温度足够高，退火过程足够慢，算法就能收敛到全局最优解。

2.4 改进的基于Metropolis 规则的Q学习算法

与Q学习收敛速率紧密相关的因素有

1）状态空间；

2）动作选择。

因此，要想提高Q学习的收敛速率，就需要使问题的状态空间尽可能地小，也即缩小可行解空间；以及寻找合适的动作选择策略，使得Q学习在探索和利用之间达到平衡，既避免一味的贪心利用陷入局部最优，又防止过多的探索降低学习算法的性能[12]。

针对以上两点，本文提出了一种改进的基于Metropolis的Q学习，下面给出此算法描述：

Step 1 初始化所有 W ( St,at)，情节数k=0和情节设定值K，以及t；

Step 2 随机初始化状态 S，并使其满足

Step 3 根据贪婪策略，从动作集A中选取当前状态S的值函数 W ( St, at)最大的动作ap，若W( St, at)为最大的数量超过2，则随机从对应的几个动作中选取一at作为ap；

Step 4 从动作集A中随机选取一动作ar；

Step 5 若W( St,ap)≥W( St, ar)，则a=ap；否则，产生[0,1]之间的随机数ε；如果a=ap；

Step 7 由式(1)更新 W ( St, at)；

Step 8 St=St+1，i=i+1，如果步骤数i达到设定值 I，返回 Step 2，并令 k=k+1，t=t* ( K -k)/K；若情节数k也达到设定值K，算法结束；否则，返回Step 3继续。

算法描述中Step 3至Step 5是Metropolis原则的应用，其中加入了贪婪策略，试图利用已学习到的信息采用当前最优的动作，而随机数ε的存在，又使得算法不放弃探索，以exp(ΔQ/t)的概率接受新的动作尝试。随着温度t的降低，探索成分将极大减少，最终几乎不存在探索。在探索中，算法采用随机选取相同最大 W 值动作的做法，旨在保证每步训练动作完全随机选择，使得结果训练序列无限频繁的访问每个动作—状态转换对，确定学习到W函数，以及最优策略[12]。

Step 2和Step 6意在缩小状态空间，对于图1所示的7个任务和3个处理机的任务调度问题，总的状态空间为221，但采用了Step 2和Step 6的限定，状态空间为 37-27×3+3=1806个，不足211，使得状态空间达到了指数级的下降。虽然算法在状态判断中会花费时间，但相比于在K×I步循环中更新所有状态空间的W值时所花费的时间，可忽略不计。

3 实验对比与分析

为了验证和比较本文算法，采用文献[8]中的调度实例进行试验。该设计任务由7个子任务节点组成，任务之间的约束关系如图1所示；3个处理机，矩阵如表1所示。

算法中用到的主要参数均采用文献[8]所用参数：折扣因子 γ = 0 .9，权重参数λ=0.85，学习率α=0.1，初始温度t =500，K=30。本算法最终收敛于8，也即最好调度策略的执行时间为8。并且找出了所有解，其对应的TPm×n为

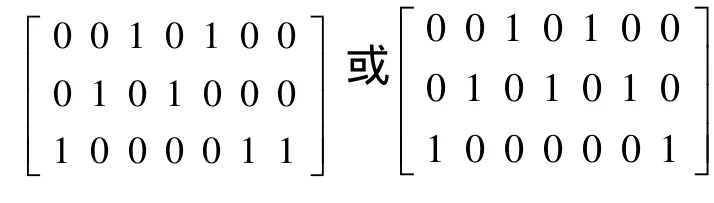
表1 子任务i在处理机j上的平均运行时间

表2给出了本算法在取不同步骤时收敛到最优解8的平均执行时间。图2所示的是本文算法与文献[8]给出的两种Q学习算法的性能比较，从中可以很明显的看出本文的改进 Q算法在时间效率和收敛速度上的较大优势（实验在普通 PC上运行，CPU2.6GHZ，内存768MB，VC 6.0）。作者猜想算法间如此大的差别可能是状态空间不同，文献[8]中的两种算法状态空间均为 221，这就意味着Q学习几乎要更新221个W值，并在此庞大的状态空间中不断搜索查询，而本文的算法加入了状态判断，使状态空间缩小到1806个，从而大大减少了搜索时间，也使得算法的执行时间获得了指数性的下降。从图2还可以看出文献[8]中的两种算法均随着步骤数的增加，收敛速度加快，执行时间变短。这一点在本文的改进Q中也有体现出来，如图3所示，随着步骤数的增大（从200到1000），情节数递减，收敛速度加快，但执行时间并没有相应的变短，原因在于步骤数i =200时，Q学习已经在情节数平均k =25处收敛于最优值。因此，随着步骤数的提高，虽然收敛速度在加速，理论上出现最优解的时间变短，但增大的步骤数所带来的搜索空间变大，各状态W值更新增多的时间花费淹没了上述改变，所以从整体上看执行时间反而有增加的趋势。

表2 不同步骤收敛到最优解的平均执行时间

图2 本算法与其它算法性能比较

图3 不同步骤数算法收敛速度比较

本文的改进 Q学习算法还与目前广泛使用的几种遗传算法做了相应的比较分析。由于经典遗传算法在进化代数达到1000时，14是作者得到的最好效果[13]，并没有求出调度问题的最优解8，因此本文另采用了文献[14]提出的两种改进的遗传算法——AGA和 GASA，与本算法进行对比。AGA和GASA均使用原文献中提供的参数，进化代数为200，初始种群为100；本文改进Q步骤数i =200，情节数k =30。图4给出了3种算法的性能对比，从中可以看出GASA和AGA比经典遗传算法在求解任务调度问题上有了明显的改进，其中GASA比AGA算法有更好的求解能力和收敛性。但不管是AGA还是GASA在时间效率上均远远大于本文的改进 Q算法。AGA最好效果是8，平均解是9，平均执行时间为103.6秒；GASA均得到最优解8，平均执行时间为112.7秒；改进Q学习算法也均收敛到最优解8，平均执行时间为9.7秒，如表3所示。因此，本文提出的改进 Q学习算法在任务调度问题的求解上有着更好的效果。

图4 改进Q与AGA、GASA的性能比较

表3 AGA、GASA与改进Q的计算结果

4 结束语

本文针对协同工作中的任务调度问题，建立了MDP模型，在此基础上提出了一种改进的基于Metropolis 规则的Q学习算法。该算法通过引入Metropolis 原则，并结合贪婪策略，既考虑了当前最优，又根据温度随机地选取其他解以增加探索的机会，确保了算法能够尽快在全局寻得最优解。为提高Q学习的收敛速度，算法加入了特定状态的筛选，使得状态空间达到了指数级的下降，从而大大加快了收敛速度，缩短了执行时间。最后本文通过和文献[8]、文献[14]中实例的对比分析，验证了算法的高效性和优越点。由于本文提出的改进Q学习算法属于静态调度算法，因此下一步的研究方向将着重于如何有效解决动态任务调度问题。

[1]冷 晟, 魏孝斌, 王宁生. 柔性工艺路线蚁群优化单元作业调度[J]. 机械科学与技术, 2005, 24(11):1268-1271.

[2]Xie Rong, Rus D, Stein C. Scheduling multi-task agents[C]//Proceedings of the 5th International Conference on Mobile Agents, 2001: 260-276.

[3]耿汝年, 须文波. 基于自适应选择遗传算法的任务调度与分配[J]. 计算机工程, 2008, 34(3): 43-45.

[4]Deepa R. Srinivasan T. Miriam D D H. An efficient task scheduling technique in heterogeneoussystems using self-adaptive selection-based genetic algorithm[C]//Parallel Computing in Electrical Engineering, 2006: 343-348.

[5]Loukopoulos T, Lampsas P, Sigalas P. Improved genetic algorithms and list scheduling techniques for independent task scheduling in distributed systems [C]//Parallel and Distributed Computing,Applications and Technologies, 2007: 67-74.

[6]Wei Yingzi, Zhao Mingyang. Composite rules selection using reinforcement learning for dynamic job-shop scheduling robotics[C]//Automation and Mechatronics,2004 IEEE Conference on, 2004: 1083-1088.

[7]Shah K. Kumar M. Distributed independent reinforcement learning (DIRL) approach to resource management in wireless sensor networks [C]//Mobile Adhoc and Sensor Systems, MASS 2007, IEEE Internatonal Conference on, 2007: 1-9.

[8]陈圣磊, 吴惠中, 肖 亮, 等. 系统设计任务调度的多步Q学习算法[J]. 计算机辅助设计与图形学学报,2007, 19(3): 398-402.

[9]Liu Xiaoping, Shi Hui, Lu Qiang, et al. Visual task-driven based on task precedence graph for collaborative design [C]//Computer Supported Cooperative Work in Design, CSCWD 2007. 11th International Conference on, 2007: 246-251.

[10]王雪松, 田西兰, 程玉虎, 等. 基于协同最小二乘支持向量机的Q 学习[J]. 自动化学报, 2009, 35(2):214-219.

[11]Christopher J C H, Watkins, Peter D. Q-learning [J].Machine Learning, 1992, (8): 279-292.

[12][美]Tom M M著. 机器学习[M]. 曾华军, 张银奎,等译. 北京: 机械工业出版社, 2003: 251-268.

[13]殷国富, 罗 阳, 龙红能, 等. 并行设计子任务调度的遗传算法原理与实现方法[J]. 计算机辅助设计与图形学学报, 2004, 16(8): 1122-1126.

[14]石 慧, 刘晓平. 协同设计中的任务调度算法及实现[J]. 中山大学学报(自然科学版), 2008, 47(6):52-56.