求解矩形布局问题的自适应算法
2012-07-07王金敏王保春朱艳华
王金敏, 王保春, 朱艳华
(1.天津职业技术师范大学天津市高速切削与精密加工重点实验室,天津 300222;2.山东英才学院,山东 济南 250104)
布局问题[1]是指满足必要的约束条件下,在布局容器中通过有效合理的方法放入若干个待布物体,并且达到某种最优指标。布局问题广泛应用于机械制造、皮革服装、造船、交通运输、航空航天等诸多领域。好的布局方案,可以提高产品的性能,减少其制造及运输成本,对于企业的发展是至关重要的。从理论上讲,布局问题属于NP-Hard问题,是一种复杂的组合优化问题。
随着计算机技术的不断发展,国内外的专家学者对矩形布局问题进行了研究并取得了一定的成果。如Dagli[2]结合人工智能与运筹学方法,提出了基于知识求解矩形件、异形件布局问题的系统概念模型。Leung T W和Yung C H等[3]分别把遗传算法和模拟退火算法这两种启发式方法运用到二维无约束一刀切问题的求解中,并通过大量的算例进行了比较。Loris F[4]利用模拟退火算法对无约束一刀切问题和约束一刀切问题分别进行了讨论。黄文奇,陈端兵[5]利用拟物拟人的思想策略,提出了基于最大穴度优先的拟物拟人矩形布局算法,并经过测试证明了其算法的高效性。Fang Hui等[6]针对矩形切割问题设计出一种改进的遗传算法,并通过实验认为该方法在很短的时间内便可以找出较好的布局结果。此外,还有很多人采用各种启发式算法,如郭乙运,刘天亮等[7]的矩形物体布局问题的实用算法中采用定序规则、摆放规则、定位规则和空间合并的策略,提出了一种基于空间分解的二维矩形物体布局的启发式算法。
与已有研究侧重优化布局定序规则不同,本文针对二维矩形布局问题,基于动态吸引子[8],以定位参数的优化为依据,提出了一种将遗传算法和模拟退火算法相结合的自适应算法。
1 问题描述
矩形布局问题描述:对于已知大小的矩形布局容器B和n个已知大小的待布矩形,通过一种有效合理的方法把这n个矩形尽可能多的放入到容器B中,并使容器的面积利用率尽可能的大,且要求任意两块放入容器的矩形块相互不能发生干涉。
若布局容器的面积为S,第i个布入的矩形块的宽和高分别为wi和hi,布局容器的面积利用率设为 f,则有
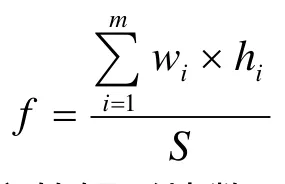
其中,m为布入的矩形块数,f值的大小可用来衡量布局结果的优劣。
矩形布局问题的数学模型为

式中,W和H分别为布局容器的宽和高;(xi, yi)和(xj, yj)分别为第i个和第j个布入矩形的中心点坐标且i≠j,这里令布局容器的左下角为坐标原点(0, 0);wi与hi和wj与hj分别为第i个和第j个布入矩形的宽与高。式(1)和式(2)说明布局物体需要完全布入到容器中,式(3)和式(4)说明两布局物体之间不能发生干涉现象。
布局求解的构造法主要是由定序规则和定位规则所决定的,定序规则和定位规则的不同可以产生出不同的构造布局算法。本文按照待布矩形的面积从大到小的顺序来确定待布矩形布入布局容器的先后顺序,若面积相等则按长边从大到小来确定布入的先后顺序。
本文采用“吸引子”的方法[8]来确定矩形块的摆放位置,即定位规则。
矩形块i的定位函数具体形式为

gt(xi, yi)为关于各个吸引子的定位函数,p为吸引子的个数。(xi, yi)为矩形块基点的坐标,(x0t,y0t)为第t个布局吸引子的坐标,αt, βt, ωt为权重因子,αt+βt=1, ω1+ω2+ω3+ω4=1。这里t =1、2、3和4且分别表示吸引子位于布局容器的左下、右下、右上和左上4个角点。
由于定位函数中参数值的不同选取将决定布入矩形的摆放位置,因此问题已转化为多参数的优化问题。本文对4个吸引子的情况进行研究,而对于其他情况,可以由4个吸引子的情况转化得到。此时,需要对定位函数中的α1、α2、α3、α4、β1、β2、β3、β4、ω1、ω2、ω3、ω4共12个参数进行优化,但由于各权重因子之间的关联关系,故实际上只需要对定位函数中α1、α2、α3、α4、ω1、ω2和ω3这7个参数进行优化。
2 自适应算法
2.1 算法原理
本文所说的自适应主要是指算法根据不同的布局容器和待布入矩形以及搜索过程,自动的调整算法的遗传、交叉、变异概率及系统接收劣质解的概率,使算法向着最优解的方向改变。
通常对于遗传算法,初始种群中个体数量的确定,交叉概率和变异概率的确定等对算法的性能是至关重要的。而对于模拟退火算法,初始温度的选择和降温策略以及接受劣质解的概率,同样具有关键的作用。若对这些操作选择不当,将不可避免的引起局部最优问题和延长搜索的时间,从而限制算法的性能。自适应的混合算法将根据问题规模的不同,对算法的种群数进行调整。当问题规模较小时,种群也较少,从而缩短搜索时间,加快求解的速度。在本文中,交叉、变异概率均采用自适应的方式,这样将有利于提高算法的收敛速度。同时,模拟退火算法中接收劣质解的概率也将采用自适应的方法进行确定。
2.2 基本操作
编 码 本文采用实数编码的方式,变量为七维的解向量,并且每一个分量都在有限的区间上定义,编码向量表示为

式中,t为进化代数,k∈[1, m]且为整数,m为种群数。
适应度函数 本文的适应度函数为容器的面积利用率 f。显然,适应度值越大,也就是布局容器的面积利用率越大,个体的性能越好。
初始种群 在初始种群确定以前,为了得到较好的结果并提高算法的整体计算效率,以随机的方式生成一个规模远远大于初始种群数的种群V。在确定初始种群数后,把种群V中个体适应度较大的个体复制到初始种群中。这样做,虽然刚开始时间增长,但是整体优化算法的代数将可以大大减少,从而提高了算法的计算效率。
在本文中,初始种群的个体数量将采用以下两种方式得到:
1)根据问题的规模大小,假设待布矩形的个数为n,那么种群中个体数量T 将由 n取整得到。这样做的好处在于当问题规模较小时,种群数也将不需要很大的值,从而提高算法的搜索效率。
2)采用预先设定固定数值的方法确定出种群数。
操作 操作是指选择操作、交叉操作、变异操作、温度的设定和Boltzmann概率等。
在进行交叉操作之前,首先对当前种群中适应度最大的个体进行保留操作,也就是在不进行任何操作的情况下,让适应度最大的个体直接进入下一代。这样做的主要目的是为了保证种群中的优良个体不被破坏,同时也保持了种群的多样性。接下来采用轮盘赌的概率选择法根据将要进行交叉的个体数目,选择出需要进行交叉操作的个体。
在通常的交叉操作中,由于算法具有很强的随机性,从而降低了本身的效率。本文将采用自适应的交叉概率来进行交叉操作。
交叉概率通过下式求出

式中,Pc1为劣质个体的交叉概率,Pc2为种群中最大适应度值的个体的交叉概率。fmax为当前群体最大适应度,favg为群体的平均适应度,f’为要交叉的两个个体中较大的适应度值。
交叉操作的具体过程如下:
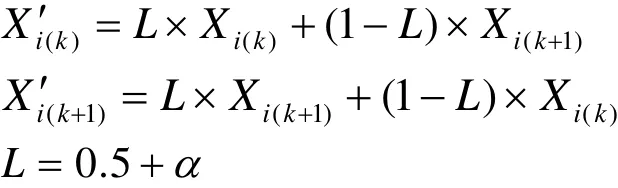
其中,α为(0, 1)之间的随机数。
由于种群中个体是向着最优解的方向进化的,在进化了一定代数后,可能会出现两个个体较为相似甚至相同的情况。此时,若再对他们进行交叉操作,将很难产生新的子代个体,为此在算法进化了一定代数后,将根据两个体之间的差异性,找出差异性最大的两个体进行交叉操作,这样做将有益于保持种群的多样性。
对于个体GK和个体GL,令和分别对应他们的第i个分量,那么通过公式
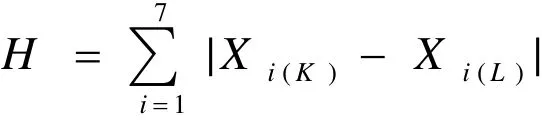
计算所得到的变量H就是种群中个体GK和GL的差异值。
对当前种群中个体进行变异操作,是产生新解和维持种群多样性的有效手段,但较大的变异概率及较小的变异概率都不利于算法的收敛。本文中变异率是随着遗传进程的变化而自适应变化的。
设Pm1为劣质个体的变异概率,Pm2为种群中最大适应度值的个体的变异概率;fmax为群体最大的适应度,favg为群体的平均适应度,f为选定变异个体的适应度值。变异概率Pm为

变异操作过程:假设选择个体Gi对其进行变异操作,首先根据变异概率Pm找出将要发生变异的分量,然后,按照以下公式进行操作,产生新的分量算子,从而产生新的个体。

式中,Xi(k)表示个体i的第k个分量,X’i(k)为变异后新个体的第k个分量,β为在整数1附近的随机数。
在遗传算法中,既要保证种群的多样性,又要使遗传算法向最优解的方向快速收敛。单一不变的群体更新方式难以兼顾遗传算法在不同阶段对多样性和收敛性的不同要求。因此,本文将模拟退火算法的Boltzmann更新机制融入到遗传算法中。
在算法搜索过程中,当子个体的适应度大于父个体的适应度时,用子个体代替父个体;否则,通过公式 q=exp(-k×△f/T) 计算出接受劣质解的概率,令C为在0和1之间的随机数,若C 其中,n为群体中个体数量,fi为个体i的适应度,favg为群体平均适应度。 在遗传算法的初期,个体间差异很大,此时T也比较大,接收劣质解的概率q也很大,可以加速遗传算法的收敛过程;当到算法的后期时,T就会变的很小,可以防止遗传算法的过早收敛。 以遗传算法为主流程,并融入模拟退火算法的Boltzmann更新机制,对定位函数中的参数进行优化。算法以布局容器的利用率和遗传进化代数作为终止判断条件。主要流程如下: 1)初始种群生成; 2)计算种群中每个个体的适应度,并计算平均适应度; 3)判断是否满足终止条件,不满足执行4),否则输出最优解,程序结束; 4)进行选择操作;5)进行交叉操作;6)进行变异操作; 8)产生新一代种群,返回到步骤2)。 在Celeron(R) CPU 2.93GHz,512MB内存的计算机上,对本文的自适应混合算法用VC++编程实现,并进行了算例的计算。 1)为了验证算法的可行性,以及定位函数中各参数的作用,对文献[10]的算例1进行求解。布局空间为40×15,待布局矩形块数为25。经计算,布入物体所占面积为546.3,容器的面积利用率为91.05%,而文献[10]的结果为88.86%。可以看出,本文的布局结果优于文献[10]中的结果。此时,定位函数各参数值分别为: 2)采用本文的自适应算法,对文献[11]中名为BENG1-BENG10的10个算例进行求解计算,可以得到如表1所示的布局结果。 表1 对比结果 从表1中可以看出,采用本文算法对文献[11]中的问题进行求解,所有问题的求解结果均优于文献[11]中的结果,其中有6个问题的布局结果为100%,最差的布局结果为96.80%。 3)采用文献[12]中的待布矩形块数和布局容器都不相同的6个实例(如表2所示),对本文中两种初始种群群体规模的确定方式进行了分析比较,结果如表3所示。 表2 布局数据 表3 两种确定种群数方式的比较 表3方式1中种群的个数是根据问题的规模大小,对待布局矩形块个数开二次方并取整得到的,方式2中种群数采用预先设定的方法定为25。从表中可以看出,采用方式1得到的种群数较方式2得到的少,在其他条件都相同的情况下采用方式2得出的容器面积利用率要高于方式1。 本文以动态吸引子定位函数为依据,采用自适应的方式对定位函数中各个参数进行了优化。关于二维矩形布局问题中定位函数参数优化的自适应混合算法,是模拟退火算法和遗传算法的有效相结合,采用大面积优先的定序原则,对待布矩形在布局空间中的位置进行了定位计算。通过算例分析,采用该方法对定位函数进行优化,是一种行之有效的方法。由于问题的复杂性,本算法还需要进一步的研究和改进,以期得到更好的布局效果。 [1]唐晓君, 查建中, 陆一平. 布局问题的复杂性和建模方法[J]. 北方交通大学学报, 2003, 27(1): 12-15. [2]Dagli C H. Knowledge-based systems for cutting stock problems [J]. European Journal of Operational Research, 1990, 44(2): 160-166. [3]Leung T W, Yung C H. Marvin D T. Applications of genetic search and simulated annealing to the two-dimensional non-guillotine cutting stock problem [J].Computers & Industrial Engineering, 2001, 40(3):201-214. [4]Faina L. An application of simulated annealing to the cutting stock problem [J]. European Journal of Operational Research, 1999, 114: 542-556. [5]黄文奇, 陈端兵. 一种求解矩形块布局问题的拟物拟人算法[J]. 计算机科学, 2005, 32(10): 182-186. [6]Fang Hui, Yin Guofu, Li Haiqing, et al. Application of integer coding accelerating genetic algorithm in rectangular cutting stock problem [J]. Chinese Journal of Mechanical Engineering, 2006, 19(3): 335-339. [7]郭乙运, 刘天亮, 袁 立. 矩形物体布局问题的实用求解算法[J]. 物流科技, 2005, 28(119): 75-78. [8]王金敏, 杨维嘉. 动态吸引子在布局求解中的应用[J]. 计算机辅助设计与图形学学报, 2005, 17(8):1725 – 1729. [9]Gilmore P C, Gomory R E. A linear programming approach to the cutting stock problem [J]. Operational Research, 1961, (9): 848-859. [10]李 明, 黄平捷, 周泽魁. 基于小生境遗传算法的矩形件优化排样[J]. 湖南大学学报(自然科学版),2009, 36(1): 46-49. [11]Martello S, Monaci M, Vigo D. An exact approach to the strip-packing problem [J]. Journal on Computing,2003, 15(3): 310-319. [12]Hopper E, Turton B. An empirical investigation of meta-heuristic and heuristic algorithm for a 2D packing problem [J]. European Journal of Operational Research, 2001, 128(1): 34-57.
2.3 算法流程
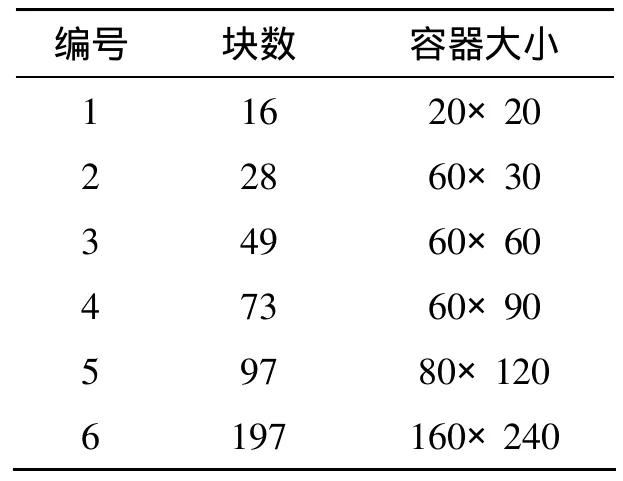
3 算例分析



4 结 论
