基于轴对称非球面元件的加工模型研究
2012-07-07张学忱曹国华聂凤鸣吴庆堂
张学忱, 曹国华, 聂凤鸣, 吴庆堂
(1. 长春理工大学机电工程学院,吉林 长春 130022;2. 长春工艺技术研究所,吉林 长春 130012)
轴对称非球面特别是其二次曲面在光学系统中的应用越来越多,其根本原因在于其面型结构简单,容易加工和检验且能有效地校正各种相差、改善像质。光学专家指出:若用一个二次非球面取代球面透镜,可使像差已成百倍的数量级减少[1]。因此,研究轴对称非球面的二次曲面模型方程及其相应参数对其加工工艺的提高有很大指导作用。
1 轴对称非球面几何模型
1.1 轴对称非球面方程
轴对称非球面的结构特点是一条母线绕一个回转轴线旋转而成为回转面、其回转面上每一点的曲率半径皆不相同。
轴对称非球面的三维图如图1所示,轴对称非球面方程一般表达形式为

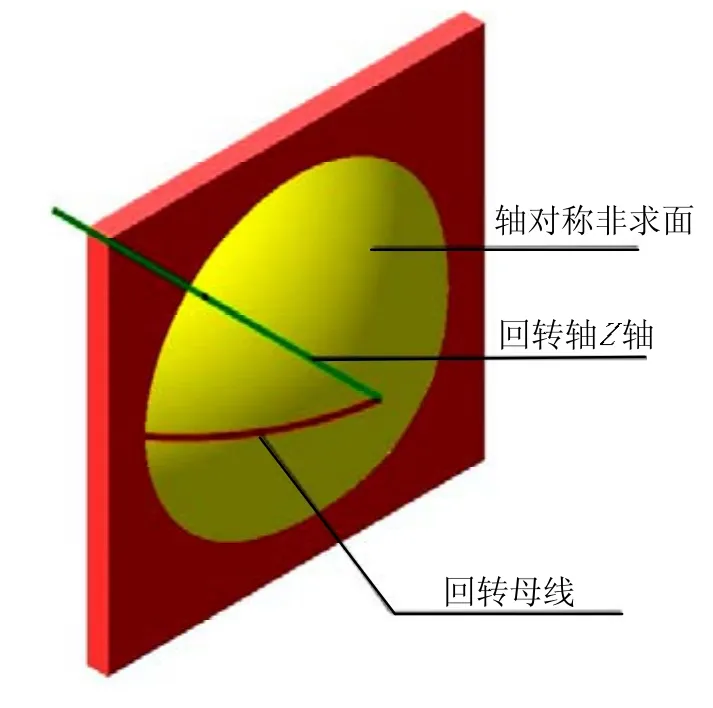
图1 轴对称非球面三维图
式中
c——曲面顶点处曲率, c = 1 R0;
R0——曲面顶点处曲率半径;
k——二次曲面偏心率函数, k =-e2,e为偏心率;
d、f、g…——方程高次项的系数;
z——为轴对称非球面的回转轴。
回转面的研究可通过回转母线的研究使问题简化,轴对称非球面中的回转母线是其子午截线,方程为

式(2)取右边第一项时表示二次曲线,且当k取不同值时代表不同的二次曲线。通过变换可以求出二次曲线方程的表达形式为

1.2 起始球面与非球面度
在加工非球面之前,首先要计算出一个起始球面,这个起始球面与欲加工的非球面最为接近,所以有时又被称为比较球面。非球面度是指某一非球面和起始球面在沿旋转轴(光轴)方向的偏差。非球面度的大小反应加工的难易程度,同时非球面度的大小也决定着加工进给量的制定和加工速度的确定。
1.2.1 非球面度的计算
在磨削加工中,要求起始球面应通过非球面的顶点O(图2),此时轴对称非球面的球心必在非球面的回转轴上,设球心坐标为 A ( 0,0,R),沿非球面法向的非球面度为δ,则
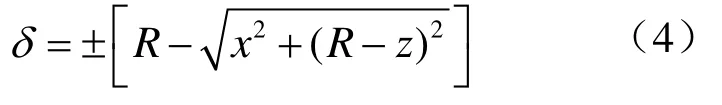
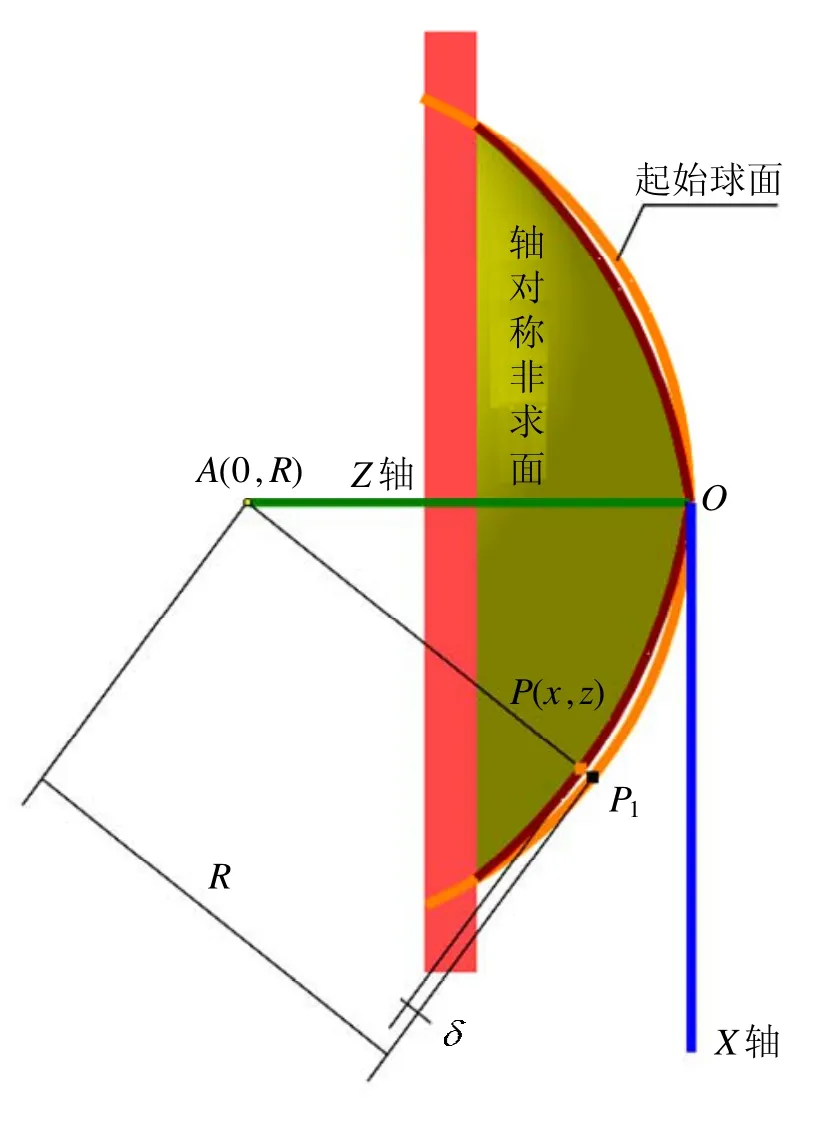
图2 凸轴对称非球面与初始球面的非球面度(沿法向)
式中R为非球面的起始球面半径,它与轴对称非球面顶点处曲率半径R0相同; (x, z)为非球面上任一点P的坐标。
对于凸非球面,上式取正号,保证非球面度为正,此时凸非球面的起始球面位于远离回转轴的非球面一侧。图2中P1为过P点法线延长线上起始球面上的点。
非球面度是在对非球面进行加工前要确定的一个重要工艺参数。在非球面度较小时,最大非球面度一般发生在
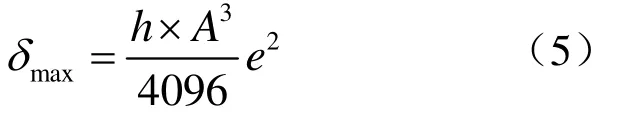
式中,A为非球面的相对口径。这样便于单方向加工,降低加工难度。当相对口径很大时,应根据非球面方程和起始球面方程作数值计算求得[2]。
1.2.2 最接近起始球面半径
求得最接近起始球面半径是磨削加工中需决定的另一个重要的工艺参数,其影响工件的实际加工余量。采用非球面与起始球面之间的最大非球面度的大小来确定起始球面半径。根据确定最接近起始球面的3个要求:非球面度为正;起始球面过非球面的顶点和使其加工余量最小,在x变量的定义域[0 , h 2]中,最大非球面度δmax获得最小值的起始球面半径R应满足的条件为

当需要加工的轴对称非球面方程为已知,则非球面度δ是关于起始球面半径R和非球面坐标X的二维函数;最大非球面度函数δmax是R的一维函数。
对轴对称非球面磨削加工时的砂轮轨迹为最接近起始球面,位移机构的进给方向与该球面的法向始终相同,所以沿最接近起始球面的法线方向与非球面的偏差,即法向非球面度(图2),就是砂轮的位移机构的进给量,式(4)可以求出最大非球面度为最小时的最接近起始球面的半径R[2]。
2 轴对称非球面磨削加工模型
对于具有非球面等复杂几何形状的零件,常用的研磨抛光等游离磨料的加工方法很难保证加工精度。在实际应用中,多采用金刚石砂轮超精密磨削对轴对称非球面曲面的零件进行加工[3]。
下面以平面砂轮对凸非球面加工为例进行研究,分析磨削加工的原理,建立砂轮磨削点运动模型。
2.1 磨削加工原理
在凸非球面磨削加工中,利用两轴直线运动和回转摆动构成三轴数控联动系统实现进给运动,采用平面砂轮包络法,实现非球面的加工。
如图3所示,凸非球面磨削加工过程主要包含5个运动:工件由工件主轴带动实现回转运动;砂轮由砂轮回转轴带动绕自身几何轴线的自转;z轴向进给驱动运动;x轴向进给驱动运动;砂轮由摆动驱动系统带动实现一定角度的回转摆动运动。z轴、x轴和回转摆动这3个运动数控合成以保证砂轮始终沿非球面子午截线方向进行进给加工。

图3 平面砂轮加工非球面原理图
在轴对称非球面的磨削加工中,平面砂轮是常用的加工用砂轮之一。在平面砂轮磨削中,零件的加工过程除前面提到的运动外,还有砂轮沿y轴的进给(上下移动),使砂轮轴的轴线和工件主轴轴线共线,这是在加工前的调整工作,调整后整个磨削过程y不变,即可取y = y0。
砂轮的磨削加工,由上述的6个运动组成。砂轮磨削点运动模型就是指分析确定这些运动要素。
2.2 砂轮磨削点运动模型
在平面砂轮加工中,砂轮与被加工表面主要是点接触,所以在磨削中,平面砂轮与被加工表面是一阶点接触加工方式,砂轮中心s与加工接触点p连线沿非球面的法向。
根据磨削加工原理,设在凸非球面上建立的坐标系 xoz(图 4),机床控制中心坐标为(x, z),即砂轮中心s的坐标,子午截线上的加工点P的坐标为 (xi, zi),则砂轮磨削点加工中的控制公式为

式中,γ为子午截线在加工点P处的切线与x轴夹角,也是砂轮磨削过程中的摆动角度,即;平面砂轮半径。在实际加工中,需要先加工出与欲加工的非球面最为接近的球面(本文称为起始球面)作为磨削非球面的毛坯工件,并根据非球面度的大小定出进给量,砂轮开始磨削。在磨削过程中,为保证磨削点始终在子午截线上,砂轮要按一定规律进行摆动(图5)。

图4 磨削点几何模型
设加工非球面端口处的砂轮摆角为γmax,此时的摆角最大,其计算公式为

其中,R为非球面端口处切削点到起始球面球心的距离,这一切削点和起始球面上的点重合。
由式(8)可以算出砂轮最大加工摆角

如图5所示,当砂轮磨削到顶点时,砂轮轴摆角γ=0°;所以砂轮轴的摆角变化范围为

加工之前要确定了砂轮磨削点的初始位置,这样在整个磨削过程中砂轮上的磨削环带是固定不变的,但由于非球面的曲率沿子午截线是变化的,所以砂轮上瞬间的磨削点也是变化的,从而对磨削的进给运动的研究可以改变到对砂轮中心s的运动模型进行研究。

图5 砂轮摆动模型及摆角几何模型
2.3 砂轮中心点运动模型
理论的砂轮中心轨迹是距起始球面为砂轮半径的法向等距面,非球面加工时,砂轮与加工表面是一阶点接触,砂轮中心轨迹是距非球面为砂轮半径rr的法向等距面。在研究回转对称的非球面时,可以转化为对某个坐标面上的回转母线的研究,使问题简化。如图6所示,加工砂轮的中心移动轨迹是关于凸非球面子午截线的法向等距线。

图6 切削点和砂轮中心点S的法矢
设子午截线方程为式(2),非球面子午截线上任意一点P的单位法矢为

rs沿着点P法矢n的法向上截ps=r(r砂轮半径),则砂轮中心点 s在加工时形成的轨迹为子午截线在法向的等距曲线,其方程
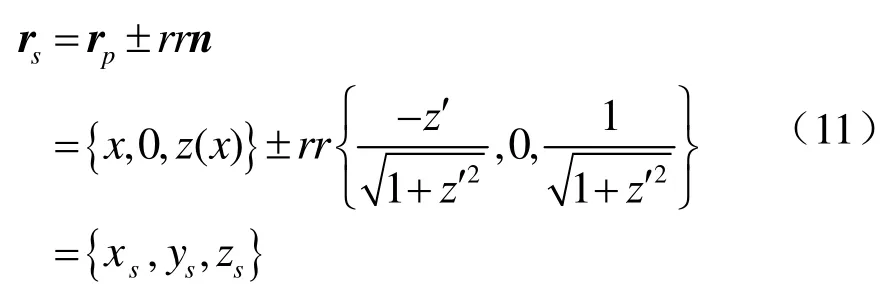
在实际加工中,砂轮中心一定在非球面子午截线的法向等距线上,式(11)表示了平面砂轮中心轨迹与被加工非球面之间的关系,其距离为平面砂轮的半径rr。
最接近起始球面方程为

其中,R为非球面最接近球面半径,则在球面上任一点的法矢为
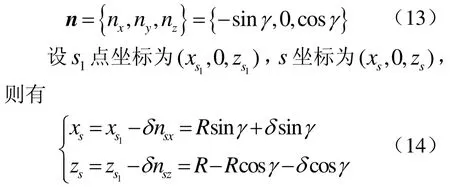
点s为非球面法向等距线上点,满足方程(11),将式(14)代人式(11),可求出进给量δ。由点P的任意性,可以得到非球面加工时任一时刻砂轮沿法向的进给量,形成非球面。
由上面分析,可求得起始球面上任一点 P1的法向与z轴的夹角γ,其确定砂轮与进给机构的转角进给,即确定平面砂轮中心与加工点连线沿法向的转角。
已知起始球面上任一点P1的法矢为式(10),Z轴方向矢为 e3=(0,0,1),则有

当确定子午截线上的任一点 P,则z′( x)为定值,由式(15)可得到转角进给量γ。
2.4 x,z 两个方向的直线进给运动
在确定平面砂轮磨削凸非球面的零件时,需要确定沿x方向和z方向的直线位移量dx, dz。以使砂轮磨削点沿子午截线进行加工。
如图7所示,设子午截线方程为式(2),砂轮由凸非球面子午截线上的q1点磨削至q2点,设q1点的坐标为 ( x1, z( x1) ), q2点坐标为 ( x2, z( x2)),则

在实际加工中,进给量是施加于砂轮中心点S1上的(图7),设在砂轮中心建立坐标系x1s1z1,则从图7可见,z1与z反向,x1与x反向,则在实际确定两个方向的直线位移量时有


图7 x,z方向进给
3 结 论
1)非球面度是反映光学非球面加工难易程度的一个重要参数,也是加工检验的重要指标,它决定着加工进给量和加工速度的制定。本研究对非球面度进行了有效而精确的计算。
2)起始球面作为加工的毛坯件是提高磨削效率的有效方法,最接近起始球面半径是加工中有别于非球面度的另一个重要工艺参数,它直接影响工件的实际加工余量,本研究推导出起始球面半径。
3)x, z两个方向的直线驱动进给分别是由工件和刀具所在的机械系统独立实现的方式给出的,其有利于减少系统误差,提高运动精度,使机床的整体结构刚性好。
4)x, z直线运动和摆动系统的回转摆动运动构成加工机床的三轴联动系统,实现了砂轮加工轴对称非球面的包络成型。为提高面型精度,三轴联动系统的控制尤为重要。
5)本论文的创新之处在于磨削加工数学模型的建立,为平面砂轮加工非球面元件提供了可行的技术方案。
[1]Shirvaikar M V, Mohan M T. A neural net work filter to detect small targets in high clutter backgrounds [J].IEEE Transactions on neural net work, 1995, 6(1):252-257.
[2]潘君骅. 光学非球面的设计、加工与检验[M]. 苏州:苏州大学出版社, 2004: 1- 63.
[3]骆红云, 焦 红. 金刚石刀具与精密超精密加工技术[J]. 长春光学精密机械学院学报, 2000, 23(1):49-54.
