基于Daubechies小波的图像边缘检测技术

毛安定， 管一弘， 段 锐， 王艳华， 吕 梁， 季云海

（1. 昆明理工大学理学院，云南 昆明 650093；2. 云南省昆明市第一人民医院，云南 昆明 650093）

基于Daubechies小波的图像边缘检测技术

毛安定1， 管一弘1， 段 锐1， 王艳华1， 吕 梁2， 季云海2

（1. 昆明理工大学理学院，云南 昆明 650093；2. 云南省昆明市第一人民医院，云南 昆明 650093）

利用Daubechies正交小波变换的性质，通过Mallat多尺度分析方法对图像进行小波变换，把图像分解成低频轮廓，水平高频、垂直高频和斜线高频四个部分。针对图像边缘主要集中在高频部分，该文先保持小波变换后的高频小波系数，同时对低频小波系数进行再次小波变换，提取出次高频信号的边缘信息。最后对保留下来的高频小波系数和次高频小波系数进行逆变换获取最大边缘信息。

Daubechies小波；小波变换；多尺度分析；边缘检测

图像边缘检测是指检测出图像局部变化不连续的区域，然后根据这一细则勾勒出图像的具体轮廓，起到图像识别的作用。图像局部化特征不连续一般指灰度值的突变，颜色的突变，纹理结构的突变，从本质上来归纳，边缘就是一个区域的终结和另一个区域的开始。对于图像分割学说来讲，研究图像边缘检测在图像识别中具有很重要的作用[1]。

然而传统的边缘检测算子只重视对图像时域的分析，忽略了频域的分析。而图像的边缘信息恰好处于频域的高频信号，那么就可以通过对频域的分析提取出图像的边缘信息。针对频域的分析，傅立叶变换是个很好的分析手段，然后在分析局部化特征上，傅立叶变换有它自身的局限性。因此，根据研究总结，本文提出根据Daubechies小波变换的多尺度分析方法提取出图像的最大边缘信息[2-3]。

1 Daubechies小波变换

根据对Daubechies小波的研究，发现它具有很好的正交性和紧支性，而且是双正交小波函数，同时支撑宽度为2N-1，滤波器长度为2N。因此，Daubechies小波对于二维图像小波变换具有很好的滤波作用，对提取图像边缘信息有重大作用[4-6]。

为把 Daubechies小波变换用于图像边缘提取，需将一维小波变换推广到二维。针对二维离散小波变换，设二维尺度函数）（yx,φ是可分离的，即

则可构造3个二维基本小波函数

式中，ψ(x)，ψ(y)分别是)(xφ，)(yφ对应的正交小波函数。上列3个二维基本小波函数的伸缩平移系表示为

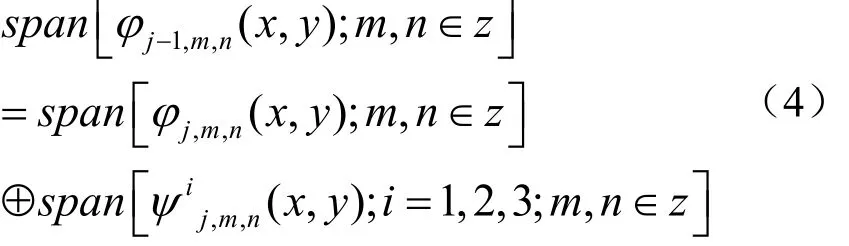
一个二维图像信号f(x,y)在尺度 2j下的平滑成分（低频分量）可用二维序列Dj(m,n)表示为

f(x,y)在尺度 2j下的细节成分（高频分量）可用以下3个二维序列表示

式（5）和式（6）表明，4个二维序列可以由f(x,y)分别沿x方向和y方向经由不同的一维滤波器滤波，并抽取偶数下标的滤波结果来得到。具体来说，f(x,y)的每一行序列用一维滤波器 φj( -x)滤波后，将所得结果的偶数元素抽取出来，然后对所得二维图像的每一列序列用一维滤波器ψj( -y)进行滤波，并抽取每列结果偶数下标的元素，最后便得到二维序列(m,n)。其余的(m,n)，(m,n)及D(m,n)的计算与此j类似[9-10]。

2 Mallat多尺度分析方法

Daubechies离散小波变换用矩阵H和G分别表示一维滤波 φj(-x)和ψj( -y)并抽取偶数下标元素的运算，并用下标r和c分别表示矩阵的行和列操作，那么可以得到二维Mallat算法公式如下

图1所示的是二维Mallat算法小波变换的分析信号流程图，图2所示的是其合成信号流程图，都只画出了一次迭代过程[11-12]。

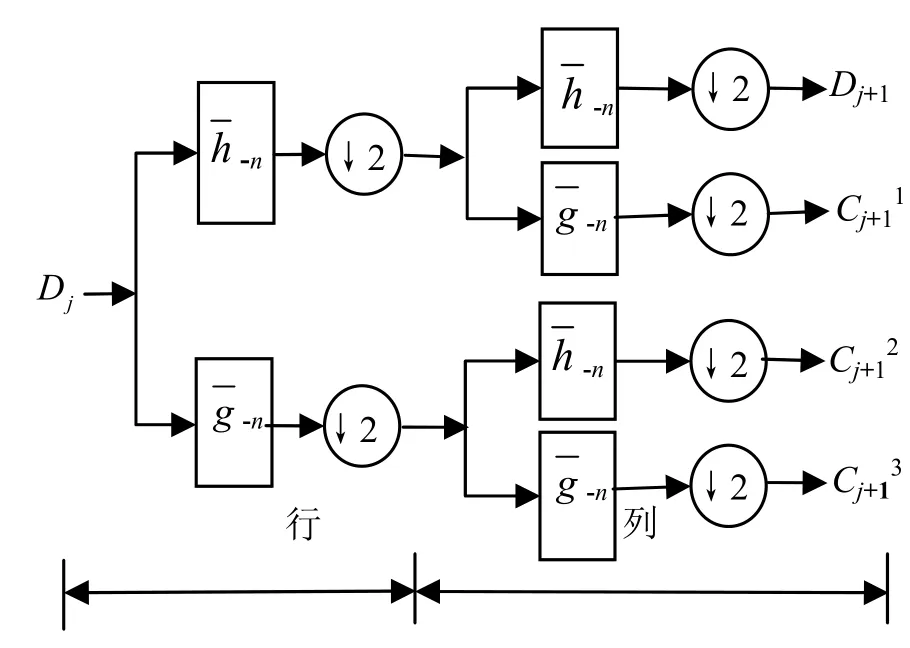
图1 二维Mallat算法分解部分

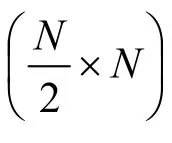
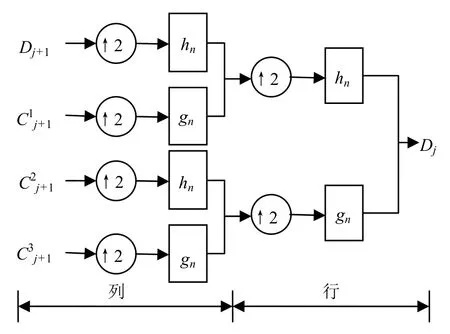
图2 二维Mallat算法合成部分

图3 小波变换频段分布

3 边缘检测算法实现

将一幅 Lena( 2 56× 2 56)图像进行二维离散小波分解后，得到4个部分的小波系数，分别如上图3所示，左上角代表图像的低频轮廓部分，右上角代表图像的垂直高频细节部分，左下角代表图像的水平高频细节部分，右下角代表斜线高频部分。Lena小波变换图像和对应的二维直方图如图4所示。

为了提取出图像的最大边缘信息，我们首先保持Daubechies小波变化后的高频细节部分；并对低频小波系数进行再次小波变换提取出次高频小波系数；最后对保持的高频小波系数和次高频小波系数进行Daubechies小波逆变换，获取最大边缘信息。边缘检测流程图如图5所示，边缘检测结果如图6所示。

图4 Lena小波变换图和对应二维直方图

图5 边缘检测流程图

4 结 论

图6 边缘检测结果

利用 Daubechies正交小波变换，可以分割出不同频段的图像。针对边缘信号主要集中在高频段，本文在保持高频信号的同时，并没有全部丢失低频信号，而是对低频信号进行再变换提取次高频信号。这样保证了最大限度地提取出高频细节信号，为最后逆变换提供了更多的高频信号。实验结果证明，图像边缘信息被最大范围提取出来，没有断开不连续的点，而且很多局部细节信息也被很好的表现出来，为下一步图像识别技术提供了很好的技术平台。本文创新点之一是利用了 Daubechies小波的正交性和紧支性溶入到图像处理中；另一创新点是该方法并没有完全丢弃低频轮廓信息，相反是最大程度提取高频信息；这样既保持了高频信号，又提取了低频信号中的次高频信号，保持图像边缘信息的完备性。

[1]姚天任, 孙 洪. 现代数字信号处理[M]. 武汉：华中理工大学出版社, 1999：209-293.

[2]丁玉美, 高西全. 数字信号处理[M]. 西安：西安电子科技大学出版社, 2006：4-146.

[3]阮秋琦. 数字图像处理学[M]. 北京：电子工业出版社, 2007：1-2.

[4]陈武凡. 小波分析及其在图像处理中的应用[M]. 北京：科学出版社, 2002：175-178.

[5]朱 虹, 等. 数字图像处理基础[M]. 北京：科学出版社, 2005：186-236.

[6]夏良正. 数字图像处理[M]. 南京：东南大学出版社,1999：1-42.

[7]章毓晋. 图像分割[M]. 北京：科学出版社, 2001：1-195.

[8]康耀红. 数据融合理论与应用[M]. 西安：西安电子科技大学出版社, 1997：1-27.

[9]曾 欢, 王 浩. 图像边缘检测算法的性能比较与分析[J]. 西安：现代电子技术, 2006, (14)：53-58.

[10]崔锦泰. 小波分析导论[M]. 西安：西安交通大学出版社, 1997：24-103.

[11]孙廷奎. 小波分析及其应用[M]. 北京：机械工业出版社, 2005：55-151.

[12]胡广书. 现代信号处理教程[M]. 北京：清华大学出版社, 2003：57-180.

[13]冯象初, 甘小冰, 宋国乡. 数值泛函与小波理论[M].西安：西安电子科技大学出版社, 2003：51-184.

[14][美]Ingrid Daubechies. 小波十讲[M]. 李建平, 杨万年, 译. 北京：国防工业出版社, 2004：1-313.

Image edge detection technology based on Daubechies wavelet

Mao Anding1, Guan Yihong1, Duan Rui1, Wang Yanhua1, Lü Liang2, Ji Yunhai2
( 1. Science College, Kunming University of Science and Technology, Kunming Yunnan 650093, China;2. The First People’s Hospital of Yunnan Province, Kunming Yunnan 650093, China )

In this paper, an image wavelet transform is conducted by using the features of Daubechies orthogonal wavelet and the Mallat multi-scale analysis method. The image is decomposed into four parts of a low-frequency contour, the horizontal high-frequency, the vertical high-frequency and the slash high frequency. Because the image edge mainly concentrates in the high-frequency parts, the high-frequency wavelet coefficients are reserved while low-frequency wavelet coefficients are conducted of wavelet transform again, extracting the second high-frequency signals from low-frequency contour parts. Finally, the maximization of edge information of image is achieved in extraction by use of inverse transformation of the high-frequency wavelet coefficients and the second high-frequency wavelet coefficients.

Daubechies wavelet; wavelet transform; multi-scale analysis; edge detection

TP 301.6

A

1003-0158(2012)01-0063-05

2009-02-19

云南省自然科学基金资助项目（2005F0194m）

毛安定（1981-），男，四川泸州人，硕士，主要研究方向为图像分割与融合。

book=1,ebook=407