多层次交通网络的UE与SO混合均衡与效率损失

曾明华，肖 瑜，黄细燕

（1.华东交通大学轨道交通学院；2.华东交通大学基础学院，南昌330013）

自由市场中所有出行者从个人角度考虑选择出行成本最小化的路径，出行者之间只有自私的博弈。在没有诱导的条件下，依靠自由市场竞争所达到的用户均衡（UE）一般不能使有限资源分配达到系统最优（SO）。如果部分出行者受控于交通诱导与控制中心，在系统最优的前提下用户出行路径选择，则系统最终会趋向于一种介于系统最优和用户最优之间的状态。因此，系统中存在效率损失，但一直没有得到定量界定。文献[1]最早提出了合作系数或无政府的代价来界定交通网络中由于用户的非合作行为而导致的效率损失问题。在此基础上，文献[2]完成了一项具有代表性的工作，即，假设具有非负系数的线性阻抗函数，发现用户均衡效率损失最多为系统最优的1/3。之后，许多学者为寻找用户平衡更小的效率损失上界而进行了一系列拓展研究[3-5]。考虑到交通网络中部分出行者接受诱导中心的指挥、按照系统最优的原则选择路径，而其他出行者根据个人成本最小的原则择路，文献[6]以及文献[7]建立了刻画这种混合交通行为的变分不等式模型，推导了混合交通行为网络的效率损失上界。研究表明一般情况下的效率损失上界与具体被研究的网络结构和交通需求水平等有关。

现实中交通网络是多模式的，多层次是多模式的伴生特征，并且已有研究表明多层次交通网络具有比非层次网络更好的性能[8-9]。本文研究了具有多层次结构的交通网络中系统最优与用户均衡所构成的混合均衡情况下效率损失问题，建立了混合均衡的等价变分不等式，并分析了多层次交通网络混合均衡的效率损失上界。该研究结果表明效率损失上界与交通网络层次结构、道路路况、交通需求水平、交通诱导信息渗透率等因素直接相关，若不考虑层次性可得文献[6]与文献[2]的分析结果。

1 问题阐述及符号

考虑交通网络G=(V，E)，V为节点集合，E为区域所有路段集合。记W={w}为所有起讫点(OD对)的集合，Rw为OD对w∈W之间的所有路径构成的集合。va为路段a∈E的交通流量,为相应向量；设为路径OD对w间r∈Rw上的交通流量，记为路径流量向量。记为交通网络中边-路径关联矩阵，当边a在路径r上时，否则，；记为交通网络中OD-路径关联矩阵，若路径r∈Rw，则，否则。设路段a上的可分离的路段成本函数为ca(va)是非负可微的，并且是关于路段流量va的单调递增凸函数；ca(va)∈C，C是给定的路段成本函数类，比如C是一簇多项式函数。

假设对区域交通网络中所有路段按照功能和技术等级分为不同层次，其中代表区域中交通模式的层次集合。设X为实数集合，对每个层次赋予一个度量用以指示其对出行者的相对吸引强度，且满足，则将lℏ称为层次因子[8]。利用交通网络层次因子给出OD对w间路径r上的广义路径费用

出行费用的选择受到用户学习和选择行为的影响，可参考文献[10]。

由于交通系统中存在安装有先进交通信息系统（ATIS）和无ATIS装置的两类出行者，他们各自遵循SO和UE两种不同的路径选择原则，这种混合交通行为将导致混合均衡。假设OD对w上的市场渗透率皆为满足某种分布，本文采用常用的均匀形式，即。若OD对w之间的交通需求量为qw（记为相应向量），则有装置用户的OD需求量为λqw，无装置用户的OD需求量为。下文用标记“”和“”分别表示有装置和无装置用户的相关变量，例如，表示有装置用户的路径流量和路段流量，和表示有装置用户的路径流量向量和路段流量向量。不妨记路段a上混合交通流为，记路径r∈Rw上的混合交通流为，并记为相应的向量。

2 多层次交通网络混合均衡及其变分不等式

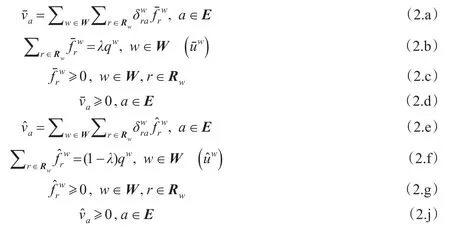
层次交通网络混合均衡，是具有多层次结构交通网络中部分用户追求系统最优而其他用户追求用户平衡所达到的一种均衡状态；满足系统最优条件的出行者内部，没有任何出行者可以通过单方面改变出行路径来降低其最小综合出行费用，而对于满足层次均衡条件的出行者而言，都不能通过单方面改变出行路径来减少其最小出行费用。其中，系统最优条件和层次均衡条件如下

1）系统最优条件

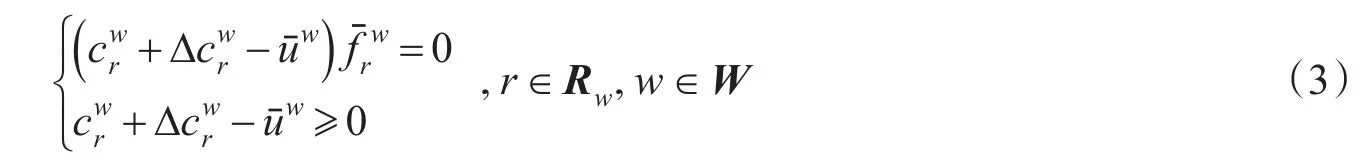
2）层次均衡条件[9]

该条件的解释：若OD对w间路径r上没有交通流，则路径r的层次路径费用不小于最小层次路径费用；若OD对w间路径r上有交通流，则路径r的层次路径费用等于最小层次路径费用，且交通流选择尽可能多包含较高层次路段的路径。

定理1设路段费用函数是关于的单调递增凸函数，则多层次交通网络混合均衡等价于：求，使下述变分不等式成立

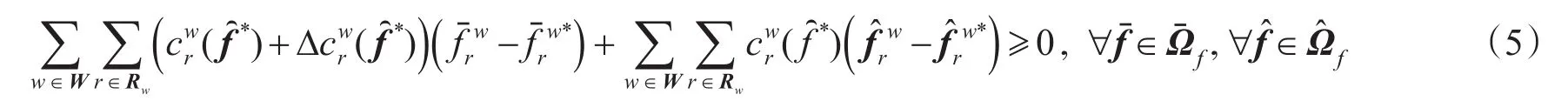
证明由变分不等式模型的Karush-Kuhn-Tucker条件，知

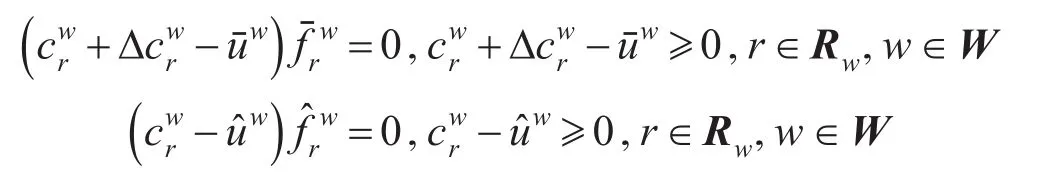
即为交通网络混合平衡条件，故有结论。

3 多层次交通网络混合均衡的效率损失上界

以下分析多层次交通网络混合均衡的效率损失上界。

将fS分解为，则代入定理1中的变分不等式并整理，可得

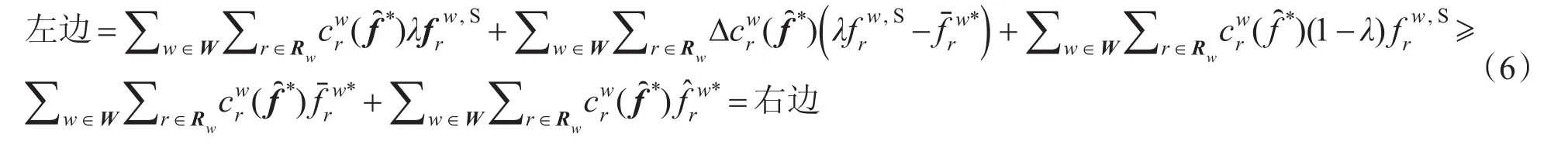
根据城市道路网络中各层次道路子网络即支路子网络、次干路子网络、主干路子网络的比例构架呈现从底到顶的金字塔型式，因此，较低层次道路子网络的车辆出行总费用在一般情况下会较高。于是，结合式（1），式（6）不等号右边的式子

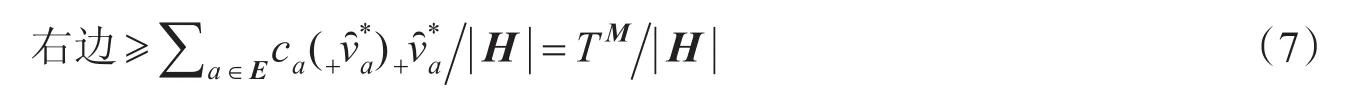
而（6）式不等号左边的式子

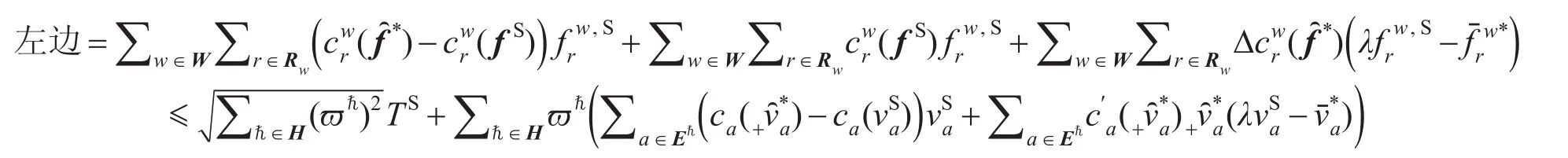
于是，（6）式变为

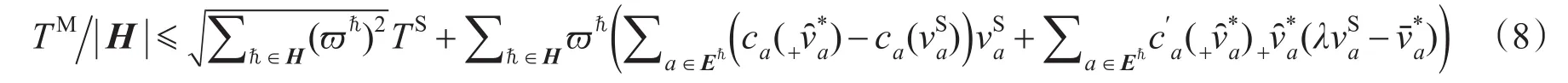
对某个层次，对属于该层次的每条路段定义参数

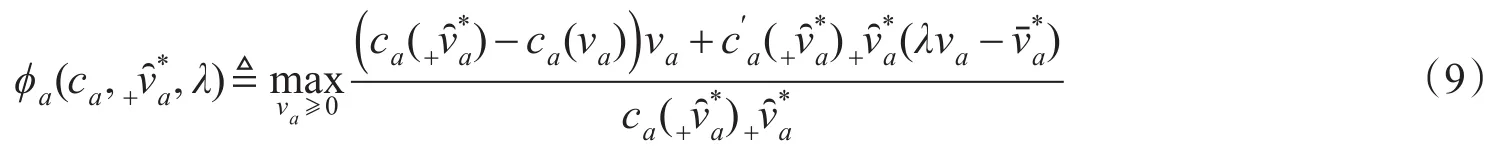
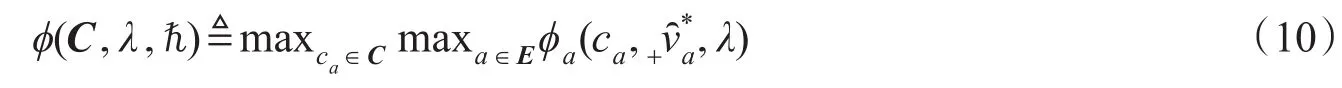
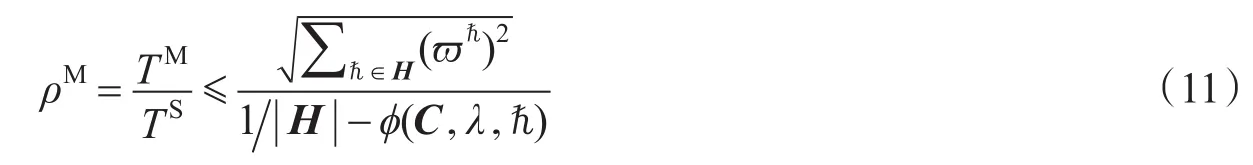
于是，得到下述混合均衡效率损失上界定理如下。

定理2假设可分离的路段费用函数ca(va)是单调递增的凸函数，所有ca构成一个函数类C；设受控于交通诱导中心的用户占交通网络总需求的比例为λ∈(0，1)，系统最优与用户平衡行为共同作用下的混合均衡的路径（路段）流量解分别为；并设交通网络系统最优的路径（路段）流量解为。那么混合均衡的效率损失存在如式（11）所示的上界。

效率损失上界与交通网络层次性结构、受控于交通诱导信息的出行者比例、路段成本函数类型等因素相关。上述效率损失上界界定了在最坏情况下交通网络的性能，由于现实交通网络中路段零流成本ca(0)＞0，考虑到这一点[3]，现实交通网络的效率损失要更小一些。沿用定理2的符号，类似于文献[6]，下述定理给出了一个更精确的上界。

定理3对，假设存在依赖于混合均衡流量的，使得零流成本满足。那么混合均衡与系统最优的网络总成本之比ρM存在如下上界

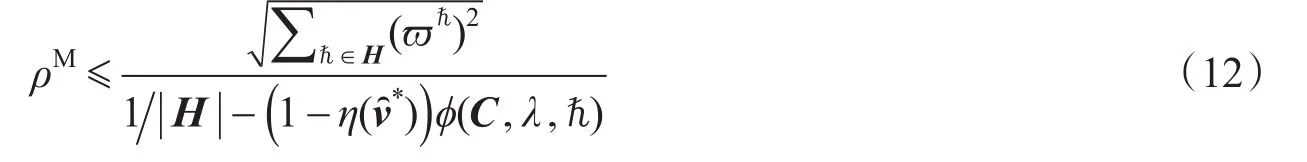
4 多项式路段费用函数情形下的效率损失上界

沿用定理2的符号和定理3中假设，定理4将给出采用常用的BPR路段费用函数情况下更吻合实际的上界。

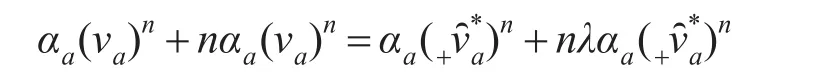
解之，即得

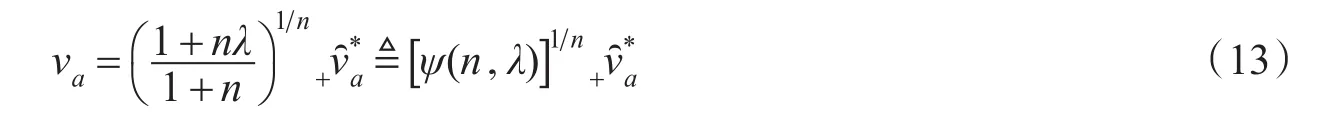
从而，将va的解代入（9）和（10）式，有

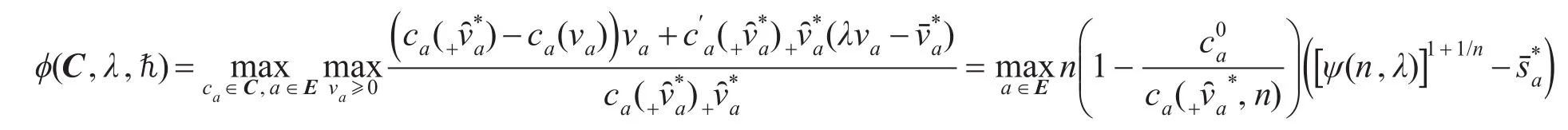
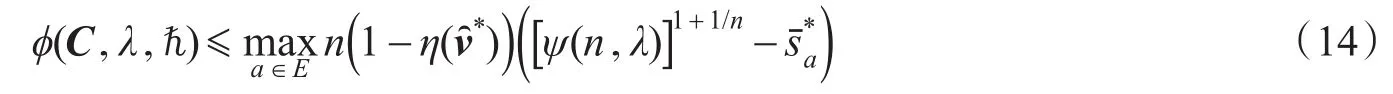
，都依赖于混合均衡流量解，且该解是与交通网络层次性结构直接相关，为了显性地表达此含义，令。从而，得到路段费用采用BPR函数时的交通网络混合均衡效率损失上界

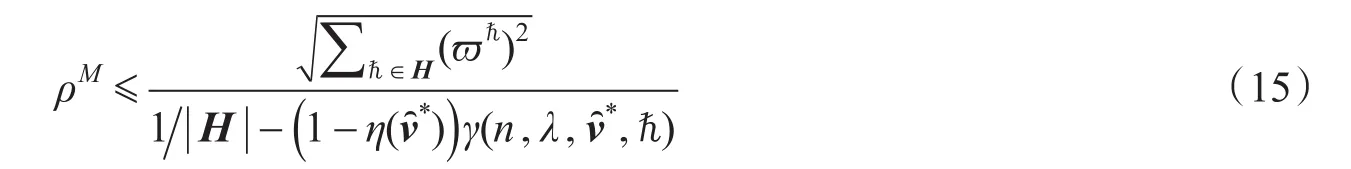
定理4取BPR函数即（自然数集），那么交通网络混合均衡的效率损失上界如上面的式（15）所示。

推论1在多层次交通网络中，假定不存在交通诱导与控制中心以保证网络中部分车辆按系统最优方式选择出行路径，则在该类交通网络中效率损失上界为

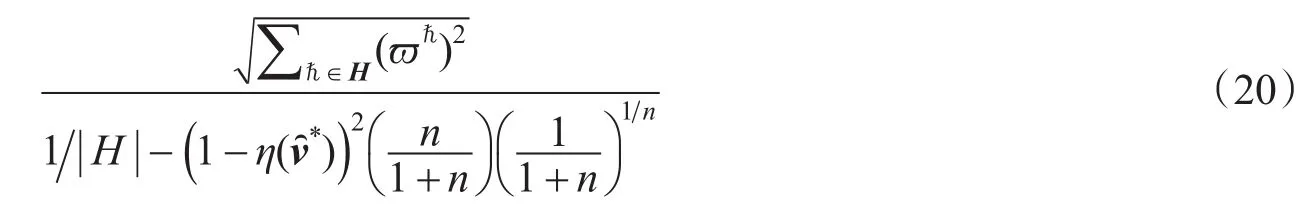
证 明由 推 论 中 的 假 定 知λ=0 ，则。 于 是 ，，故有效率损失上界如（16）式。

推论2若不考虑交通网络层次性，则交通网络混合均衡的效率损失为

稍作说明，推论2与文献[6]所得结果一致。

证明在交通网络没有层次结构的情况下，所有路段处于同一层次，即 ||H=1。且因为没有层次性，路径费用函数不用层次因子加权，仍按通常的表达方式进行计算，即（1）式变为，从而根据定理2和定理4的推导过程，可知式（17）成立。式中，是在不考虑层次结构情况下的表示 ，因为此时已与层次结构无关 ，自然与层次结构无关 ，所以，

根据推论2，进一步假设λ=0，则

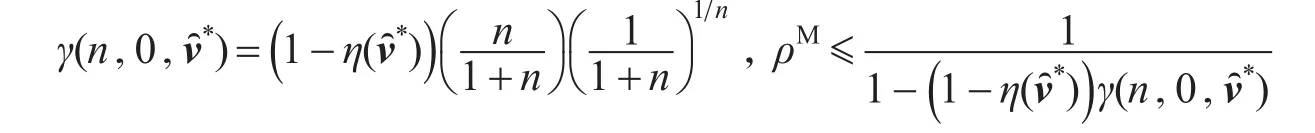
若还不考虑定理中关于零流成本ca(0)的假设，即，那么可得当n=1时，即有，这与文献[2]的结果一致。

5 结论

交通诱导信息在某种程度上提高了交通效率，降低了交通拥堵，但人们自私的出行行为使得交通网络无法达到理想的系统最优状态。给出了多层次交通网络中混合均衡的等价变分不等式及效率损失上界，交通网络效率损失上界与层次结构、交通需求水平、交通诱导信息渗透率、道路状况等多种因素有关，研究方法具有较强的现实意义。此外，流量分布还受交通需求的分布形态、交通信息的分布形态、用户出行偏好特点、交通管理政策等诸多因素的影响，因此，交通网络效率损失上界也受到这些现实因素的影响。

有研究表明多层次交通网络的性能会比传统不考虑层次性情况下所优化设计出交通网络的性能大幅提升[8-9]，因此，本文融合层次性这一反映客观实际的结构形式对交通网络的效率损失进行研究，对设计效率更高、性能更优的交通网络具有重要意义。相较于通常研究中采用的非层次交通网络，多层次交通网络究竟在多大程度上降低混合均衡的效率损失，这将是下一步的工作。

[1]KOUTSOUPIAS E,PAPADIMITRIOU C.Worst-case equilibria[C]//Proceedings of the 16th Annual Conference on TheoreticalAspects of Computer Science，Springer-Verlag，1999：404-413.

[2]ROUGHGARDEN T，TARDOS É.How bad is selfish routing[J].Journal of theACM，2002，49（2）：236-259.

[3]CORREA J R，SCHULZ A S，Stier-Moses N E.On the inefficiency of equilibria in congestion games[C]//Proceedings of the 11th International Integer Programming and Combinatorial Optimization Conference，Berlin，Germany.In：Lecture Notes in Computer Science，Heidelberg：Springer，2005，3509：167-181.

[4]石超峰，徐寅峰.交通网络效率损失上界的估计方法[J].系统工程理论与实践，2010，30（5）：945-947.

[5]黄海军，欧阳恋群，刘天亮.交通网络中用户均衡行为的效率损失[J].北京航空航天大学学报，2006，32（10）：1215-1219.

[6]刘天亮，欧阳恋群，黄海军.ATIS作用下的混合交通行为网络与效率损失上界[J].系统工程理论与实践，2007，（4）：154-159.

[7]罗文昌.界定用户平衡及Logit型随机用户平衡下的混合平衡交通网络效率损失[J].运筹学学报，2010，14（2）：79-86.

[8]曾明华，李夏苗.基于层次性的交通网络资源优化配置方法[J].中南大学学报：自然科学版，2011，42（1）：247-253.

[9]曾明华.区域交通网络层次性与优化设计[M].北京：人民交通出版社，2011：77-92，101，116-131.

[10]贺振欢.用户出行费用综合更新自学习模型的研究[J].华东交通大学学报，2010，27（1）：12-16.