时变参数动力系统的两种跟踪性质

宋晓倩,王良伟,冯玉明

(重庆三峡学院数学与统计学院,重庆 404100)

时变参数动力系统的两种跟踪性质

宋晓倩,王良伟,冯玉明

(重庆三峡学院数学与统计学院,重庆 404100)

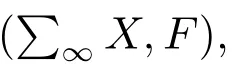
时变参数动力系统;链传递;伪轨;渐进伪轨

1 引言

经典动力系统是研究某一个映射迭代(也称为自治动力系统)所产生的动力性状,目前关于经典动力系统的研究成果已经很多,研究的主要问题围绕轨道的各种性状[1-3].如果在动力系统中,迭代的映射不是唯一的,而是随着时间而变化的一序列映射,则构成非自治动力系统,也称为时变参数动力系统.非自治动力系统的概念打破了经典自治动力系统的限制,拓展了动力系统的研究范围.由于非自治动力系统能更灵活方便的描述现实世界的各种动态和动力学行为,因此具有重要的实际应用价值.对此类动力系统的研究已逐年成为热点.1996年,文献[4]首次提出了非自治动力系统的在开覆盖意义下的拓扑熵和类似于Bowen的拓扑熵.2006年,文献[5]提出时变参数动力系统的周期点、回复性、传递性、扩张性、一致拓扑共轭等概念,并且给出了时变参数Devaney混沌系统的一个简单构造方法.2007年,文献[6]研究了线段非自治动力系统的向前熵和向后熵与逆极限空间之间的关系.2008年,文献[7]研究了非自治动力系统的预像熵.2012年,文献[8]研究了非自治动力系统的弱混合性和混沌性质.同年文献[9]研究了非自治动力系统的测度熵和拓扑熵.

伪轨跟踪性是动力系统中的一个重要概念,它与系统的稳定性密切相关,而且在数值计算中也有广泛应用.伪轨不是真正的轨道,而是一种近似轨道.关于伪轨跟踪的研究已经很多,参见文献[10-11]等.随着研究的深入,各种跟踪性质层出不穷.例如逐点伪轨跟踪[12]、周期伪轨跟踪[13]、渐近伪轨跟踪[10]、渐近平均伪轨跟踪[14]、Lipschitz跟踪及强跟踪性[15].其中渐进伪轨跟踪概念于1996年被文献[10]提出,他们研究了映射被半流渐进伪轨跟踪的动力学性质,2003年,文献[16]证明了渐近伪轨跟踪是拓扑共轭下的不变量,并且讨论了有限乘积系统的渐近伪轨跟踪性质,2006年,文献[17]研究了渐近伪轨跟踪和拓扑传递之间的关系,证明了系统满足渐近伪轨跟踪性质时,其拓扑传递和链传递是等价的.这些成果都是在自治动力系统,也就是固定参数动力系统中得出的.目前对于时变参数动力系统(非自治动力系统)的伪轨跟踪还是个未知领域,于是,下面的问题是自然的:

问题 时变参数动力系统是否也有各种伪轨跟踪性质?若有,它们的具体性质如何？

2 预备知识

2.1 伪轨概念

2.2 渐进伪轨概念

3 主要结果

[1]Li T Y,Yorke J A.Period three implies chaos[J].American Mathematical Monthly,1975,82:985-992.

[2]Bowen R.Entropy for group endomorphisms and homogeneous spaces[J].Transactions of the American Mathematical Society,1971,153:401-414.

[3]Vellekoop M,Berglund R.On intervals,Transitivity=chaos[J].American Mathematical Monthly,1994,101:353-355.

[4]Kolyada S,Snoha L.Topological entropy of non-autonomous dynamical systems[J].Random and Computational Dynamics,1996,4,205-233.

[5]Tian C J,Chen G R.Chaos of a sequence of maps in a metric space[J].Chaos Solitons and Fractals, 2006,28:1067-1075.

[6]Mouron C.Positive entropy on non-autonomous interval maps and the topology of the inverse limit space[J]. Topology and its Applications,2007,154:894-907.

[7]Huang X J,Wen X,Zeng F P.Pre-image entropy of nonautonomous dynamical systems[J].Journal of Systems Science and Complexity,2008,3:441-445.

[8]Balibrea F,Oprocha P.Weak mixing and chaos in nonautonomous discrete systems[J].Applied Mathematics Letters,2012,25:1135-1141.

[9]Zhu Y J,Liu Z F,Xu X L,et al.Entropy of nonautonomous dynamical systems[J].Journal of the Korean Mathematical Society,2012,49:165-185.

[10]BenaiM,Hirsch M W.Asymptotic pseudo trajectories and chain recurrent fl ows with applications[J].Journal of Dynamics and Di ff erential Equations,1996,8:141-176.

[11]杨润生.伪轨跟踪与混沌[J].数学学报,1996,39:382-386.

[12]Li M J.Pointwise pseudo-orbit tracing property and its application[J].Journal of Mathematics Research and Exposition,2005,25:23-30.

[13]Koscielniak P.On genericity of shadowing and periodic shadowing property[J].Journal of Mathematical Analysis and Applications,2005,310:188-196.

[14]Gu R B.The asymptotic average shadowing property and transitivity[J].Nonlinear Analysis,2007,67:1680-1689.

[15]Sakai K.Various shadowing properties for positively expansive maps[J].Topology and its Applications, 2003,131:15-31.

[16]顾荣宝,盛业青.关于渐近的伪轨跟踪性质[J].安徽大学学报:自然科学版,2003,27:1-5.

[17]Gu R B.Recurrence and the asymptotic pseudo-orbit tracing property[J].Nonlinear Analysis,2007,66:1698-1706.

Two tracing properties of timevarying discrete dynamical system

Song Xiaoqian,Wang Liangwei,Feng Yuming
(College of Mathematics and Statistics,Chongqing Three Gorges University,Chongqing 404100,China)

The purpose of this paper is to introduce chain transitivity,pseudo-orbit and asymptotic pseudoorbit for time-varying discrete dynamical system.And through these new conceptions,the pseudo-orbit tracing property and asymptotic pseudo-orbit tracing property of time-varying discrete dynamical system are studied. We proved that expansive timevarying discrete dynamical system with pseudo-orbit tracing property implies it has asymptotic pseudo-orbit tracing property.We investigate the tracing property between the product system and subsystem.It is showed that the product system has the pseudo-orbit tracing property and asymptotic pseudo-orbit tracing property if and only if each subsystem has the same property.Finally,we construct an example,which is chain transitivity and has asymptotic pseudo-orbit tracing property.

time-varying discrete dynamical system,chain transitivity,pseudo-orbit,asymptotic pseudo-orbit

O189.1

A

1008-5513(2012)05-0641-08

2012-04-07.

重庆市教委资助项目(KJ091104,KJ121105);国家自然科学基金(11126212).

宋晓倩(1985-),硕士,助教,研究方向:拓扑学动力系统.

2010 MSC:54A10