求线性矩阵方程异类约束解的修正共轭梯度法

解培月,张凯院,薛彬

(1.西北工业大学应用数学系,陕西 西安 710072; 2.中国科学院西安光学精密机械研究所,陕西 西安 710119;3.中国科学院大学,北京 100049)

求线性矩阵方程异类约束解的修正共轭梯度法

解培月1,2,3,张凯院1,薛彬2

(1.西北工业大学应用数学系,陕西 西安 710072; 2.中国科学院西安光学精密机械研究所,陕西 西安 710119;3.中国科学院大学,北京 100049)

基于求解线性代数方程组共轭梯度法的基本思想,给出求线性矩阵方程异类约束解的修正共轭梯度法,并证明算法的有限步收敛性问题.利用该算法不仅可以判断线性矩阵方程的异类约束解是否存在,而且在有异类约束解时,可通过选取特殊的初始矩阵,求得唯一极小范数异类约束解.同时,能够给出指定矩阵在异类约束解集合中的最佳逼近矩阵.数值算例表明,该算法是有效的.

线性矩阵方程;异类约束解;修正共轭梯度法;最佳逼近

1 引言

约束矩阵方程问题是在满足一定条件的矩阵集合中求矩阵方程的解,不同的矩阵方程或不同的约束条件都将导致不同的约束矩阵方程问题.此类问题在最优化设计、参数识别、自动控制、图像复原等许多科学计算领域有着广泛应用.近几年,对此类问题的研究已取得了一些成果.某些学者针对不同的方程,对未知矩阵属于同一矩阵集合的情形,采用不同的方法求得了其解或最小二乘解.如:文献[1]针对矩阵方程AX B=C,文献[2]针对一般线性矩阵方程

对未知矩阵属于中心对称矩阵集合的情形,分别采用广义奇异值分解和迭代算法求得了相应的解;针对矩阵方程AX B+CY D=E,对未知矩阵属于对称矩阵集合的情形,文献[3]建立了求其相应解的迭代算法.文献[4-5]建立了求某种特殊最小二乘解的迭代算法;文献[6]针对矩阵方程A1X1B1+A2X2B2=C的未知矩阵属于自反和反自反矩阵集合的情形,综述性的研究了求解的迭代方法.另外,针对矩阵方程组,对未知矩阵属于自反矩阵集合的情形,文献[7]也给出了相应的求解方法.可以看出,近几年中外学者对约束矩阵方程问题的研究一直没有中断.1998年,离散广义系统稳定性分析及控制中提出了Lyapunov方程在求最小二乘解的过程中,也会出现类似的某些未知矩阵相等的方程.对此,文献[8]研究了大型线性矩阵方程AX B+CX D=F的参数迭代解法.本文以双变量线性矩阵方程

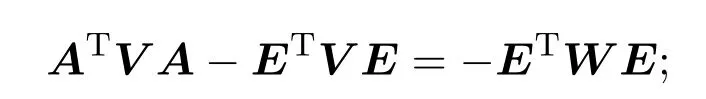
2 问题 I的迭代算法

3 问题 I的极小范数解

由引理3知,u∗是线性方程组(8)的唯一极小范数解,故(X∗,Y∗)是矩阵方程组(6)的唯一极小范数解,由定理1知(X∗,Y∗)是矩阵方程(1)的唯一极小范数约束3-7解,即问题Ⅰ的极小范数解.

综上所述,应用 MCG 3-7算法,对任意的初始矩阵 (X(1),Y(1))∈Ω3-7,若存在正整数 k,使得 Rk̸=O而 Zk=O,则问题Ⅰ不相容.若问题Ⅰ相容,则对任意的初始矩阵(X(1),Y(1))∈Ω3-7,均可在有限步计算后得到矩阵方程(1)的一组约束3-7解.特别地,若按式(7)选取初始矩阵,则可得到矩阵方程(1)的唯一极小范数约束3-7解.

4 问题 II的解

5 数值算例

用本文建立的 MCG3-7算法求矩阵方程 (1)的约束 3-7解和极小范数约束 3-7解,并给出指定矩阵在解集合中的最佳逼近矩阵 (M atlab 6.1软件 -PIV 1.50GHz微机).终止准则ε=10−9,给定矩阵

3 结论

本文以双变量线性矩阵方程为例,建立了一种适用于求线性矩阵方程异类约束解的修正共轭梯度法,理论证明了算法的收敛性,数值算例验证了其有效性.易从原理推得该算法适用于求解形式为:

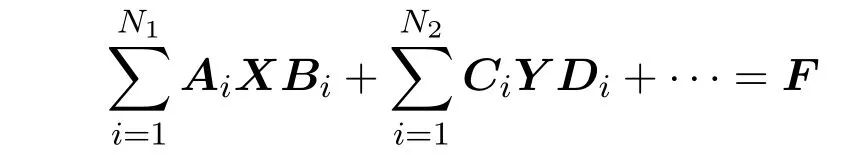
的异类约束解问题,进而拓展了该算法的适用范围.并进一步证明了MCG算法在求解约束方程问题上的优势:

(1)具有无条件收敛性,无论线性矩阵方程是否有解,该算法均能在有限步内停止;

(2)具有广泛适用性,不要求等价线性代数方程组的系数矩阵正定、可逆或列满秩;

(3)能自动判断线性矩阵方程是否有某种异类约束解,有某种异类约束解时,可以求得一组异类约束解或极小范数异类约束解.该算法用于求线性矩阵方程组的异类约束解及最小二乘异类约束解问题的工作正在进行.

参考文献

[1]彭振赟.线性矩阵方程AX B=C的中心对称解及其最佳逼近[J].工程数学学报,2003,20(6):60-64.

[2]彭卓华,胡锡炎,张磊.矩阵方程A1X1B1+A2X2B2+···+AlXlBl=C的中心对称解及其最佳逼近[J].数学物理学报,2009,29(1):193-207.

[3]Sheng Xingping,Chen Guoliang.An iterative m ethod for the symm etric and skew symm etric solutions of a linear m atrix equation A X B+CY D=E[J].Journal of Com putational and App lied M athem atics, 2010,233:3030-3040.

[4]肖庆丰,张忠志,顾广泽.广义次对称矩阵反问题的最小二乘解[J].纯粹数学与应用数学,2006,22(4):560-564.

[5]袁仕芳,廖安平,雷渊.矩阵方程AX B+CYD=E的对称极小范数最小二乘解[J].计算数学,2007,29(2):203-216.

[6]Dehghan M,Hajarian M.Finite iterative algorithm s for the reflexive and anti-reflexive solutions of the m atrix equation A1X1B1+A2X2B2=C[J].M athem atical and Com puter M odelling,2009,49:1937-1959.

[7]郑凤芹,张凯院.求多变量线性矩阵方程组自反解的迭代算法[J].数值计算与计算机应用,2010,31(1):39-54.

[8]张凯院,蔡元虎.矩阵方程AX B+CX D=F的参数迭代解法[J].西北大学学报:自然科学版,2006,36(1):13-16.

[9]张凯院,徐仲.数值代数[M].2版.北京:科学出版社,2010.

[10]张贤达.矩阵分析与应用[M].北京:清华大学出版社,2004.

The modified con jugate grad ient m ethod for d iff eren t
constrained solu tion of linear m atrix equation

Xie Peiyue1,2,3,Zhang Kaiyuan1,Xue Bin2

(1.Department of App lied Mathematics,Northwestern Polytechnical University,Xi′an 710072,China; 2.X i′an Institute of Optics and Precision M echanics of Chinese Academ y of Sciences,X i′an 710119,China; 3.University of Chinese Academ y of Sciences,Beijing 100049,China)

Based on the con jugate gradientmethod of solving linear algebraic equations,amodified con jugate gradient m ethod for finding diff erent constrained solution is given to solve linear m atrix equation,and the convergence is proved.By thism ethod,not on ly the solvability of the equation can be determ ined autom atically, but when the equation has the corresponding solution,its least-norm diff erent constrained solution can be got by choosing special initialm atrix.M eanwhile,the optim al approxim ation of given m atrix is resolved from the solution set.Finally,num erical experim ents present that thism ethod is eff ective.

linearmatrix equation,diff erent constrained solution,modified conjugate gradientmethod, op tim al approxim ation

O29

A

1008-5513(2012)06-0792-11

2011-04-28.

国家自然科学基金(11071196,60808028).

解培月(1984-),博士生,研究方向：计算数学及高光谱图像处理.

2010 M SC:65F10,15A 24