GBn链的主同余性质
2012-07-05孙中举方捷
孙中举,方捷
(广东技术师范学院计算机科学学院,广东 广州 510665)
GBn链的主同余性质
孙中举,方捷
(广东技术师范学院计算机科学学院,广东 广州 510665)
Ockham代数是一个代数(L;∧,∨,f,0,1),其中(L;∧,∨,0,1)是有界分配格,f是L上的偶格自同态.GBn代数是指一个Ockham代数(L;f),它满足条件:(fn(L);f)是布尔代数.它包含常见的布尔代数、de M ogan代数和Stone代数.本文研究了GBn链的代数结构,并给出一个GBn链具有主同余性质的充分与必要条件.
GBn代数;主同余;链
1 引言及预备知识
如果一个代数上的所有同余关系都是主同余[1],那么称这个代数具有主同余性质.例如,有限的布尔代数就具有主同余性质.1990年,文献 [1]刻画了具有主同余性质的分配格:de Morgan代数和Stone代数.1992年,文献[2]刻画了具有主同余性质的伪补代数和双重伪补代数.2009年,文献[3]刻画了具有主同余性质的一类群.虽然布尔代数、de M organ代数和Stone代数的主同余性质已经被完全地研究清楚,但布尔代数、de Morgan代数和Stone代数只是Ockham代数类中一小部分最特殊的代数子类.如何刻画整个Ockham代数类的主同余性质,这是一项艰难而持久的研究工作.目前,Ockham代数的主同余性质的研究成果就停留在布尔代数、de Morgan代数和Stone代数.为了在此领域有所突破,本文尝试研究GBn链的主同余性质.GBn代数是Ockham代数的一个较大子类,它包含布尔代数、de M organ代数和Stone代数.通过研究,给出了具有主同余性质的GBn链的充分必要条件.
回顾文献[4],一个Ockham代数,是指具有〈2,2,1,0,0〉类型的代数(L;∧,∨,f,0,1).其中(L;∧,∨,0,1)是有界分配格,运算x→f(x)是L的偶自同态.Ockham代数包含著名的布尔代数、de Morgan代数、Stone代数和K leene代数等,其与理论计算机科学的研究联系紧密,特别是在自动机和多值逻辑领域已经有较多研究.文献[5]介绍了一类广义的布尔代数,称之为GBn代数.它是Ockham代数的一个较大的代数子类,包含常见的布尔代数、Stone代数和对偶Stone代数.所谓GBn代数,是指一个Ockham代数(L;f),它满足条件:(fn(L);f)是一个布尔代数,其中n≥0,而且fn(L)={fn(x)|x∈L}.显然,GB0=B,B是布尔代数,且
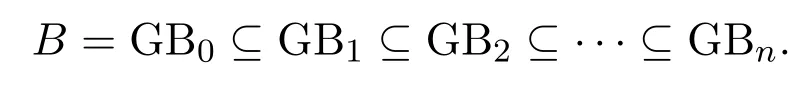
有关Ockham代数与GBn代数的基本性质,请参见文献[4-5].
设A是一个代数,H⊆A,用θ(H)表示A的包含H×H的最小的同余关系.当H={a,b}时,称θ(a,b)是A的一个主同余.特别地,对于格L,通常用θlat(a,b)表示L的格主同余.为了文中需要,给出分配格的主同余的一些基本性质如下:
引理 1.1[6]设L是一个分配格,a,b,x,y∈L,且a≤b.则
(1)x≡y(θlat(a,b))当且仅当x∧a=y∧a,x∨b=y∨b;
(2)θlat(a,b)∧θlat(c,d)=θlat((a∨c)∧b∧d,b∧d).
设(L;f)是一个Ockham代数,若θ是L上的格同余关系,且(a,b)∈θ蕴含(f(a),f(b))∈θ,那么θ是一个Ockham同余关系(简称同余关系).将用符号ω和ι分别表示相等关系和泛关系.在一个Ockham代数(L;f)中,下面所定义的L的等价关系

是L的基本同余[4].显然,有

关于Ockham代数的主同余关系,已于1977年由Berman所刻画[4,6].相关知识也可以参考文献[7-10].为读者方便起见,给出如下.
引理1.2[4]设(L;f)是一个Ockham代数.若a,b∈L且a≤b,则
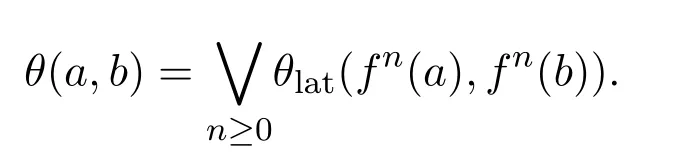

2 GBn链的主同余性质










图1 具有主同余性质的GBn链
所以定理2.4成立.
[1]B lyth T S,Varlet JC.Principal congruences on som e lattice-ordered algebras[J].DiscreteM ath.,1990,81:323-329.
[2]Beazer R.Som e p-algebras and double p-algebras having only p rincipal congruences[J].G lasgow M ath.J., 1992,34:157-164.
[3]Ikikardes S,Sahin R,Cangul IN.Principal congruence subgroups of the Hecke groups and related resu lts[J]. Bull.Brazilian Math.Soc.,2009,40(4):479-494.
[4]B lyth T S,Varlet J C.Ockham A lgebras[M].Ox ford:Ox ford University Press,1994.
[5]Fang J,Sun Z J.A subclass of Ockham algebras[J].Acta M athem atica Sinica,2012,28(10):2115-2128.
[6]G r¨atzer G.Lattice Theory[M].New York:W.H.Freem an and Com pany,1971.
[7]Berm an J.Distributive latticeswith an additional unary operation[J].Aequationes M ath.,1977,16:165-171.
[8]方捷,沈吓妹.具有Heyting结构的Ockham代数[J].纯粹数学与应用数学,2010,26(1):138-145.
[9]Fang J.Distributive Lattices with Unary Operations[M].Beijing:Science Press,2011.
[10]Sankappanavar H P.A Course in Universal A lgebra[M].New York:Sp ringer-Verlag Inc.,1981.
Principal congruences on GBnchains
Sun Zhongju,Fang Jie
(School of Com puter Science,Guangdong Polytechnic Normal University,Guangzhou 510665,China)
An Ockham algebra is an algebra(L;∧,∨,f,0,1)in which(L;∧,∨,0,1)is a bounded distributive lattice and f is a dual lattice endom orphism on L.A GBn-algebra is an Ockham algebra(L;f)with the p roperty that(fn(L);f)is a Boolean algebra,including the Boolean algebra,de M organ algebra and Stone algebra.In this paper we shall investigate the algebraic structure of GBn-chains,and give the suffi cient and necessary condition for those GBn-chains that have the principal congruence p roperty.
GBnalgebras,principal congruences,chain
O153
A
1008-5513(2012)06-0779-13
2012-05-15.
国家自然科学基金(11261021).
孙中举(1982-),博士,讲师,研究方向:格论与有序代数.
2010 M SC:06D15
