求解带尖角区域声波散射问题的三种数值处理方法

彭增军

(西北大学数学系,陕西 西安 710127)

求解带尖角区域声波散射问题的三种数值处理方法

彭增军

(西北大学数学系,陕西 西安 710127)

通过单双层位势在尖角处的跳跃关系建立了形式较为简单的边界积分方程,然后再分别利用指数变换、周期变换和K ress变换三种方法对带尖角的区域进行处理,并通过数值算例对这几种方法的求解结果进行了分析比较,最后得出周期变换效果最佳.

声波散射;带尖角区域;指数变换;周期变换;K ress变换

1 引言

声波散射问题一直以来是数学物理问题的一个研究热点,国内外许多学者对此问题进行了一系列的研究,特别是K ress教授在文献[1]中利用单双层位势的组合对这类问题做了大量的研究并且取得了很好的结果.对于带尖角区域的声波散射问题,在应用边界元方法进行数值求解时,由于双层位势在尖角处不连续,这样就导致计算结果出现较大的误差,因此引入适当的变换,使得在新的变量下双层位势在尖角处连续,从而保证数值解的精确性.文献[2-4]各给出了一种求解尖角区域的声波散射问题的方法,但在其边界积分方程中都涉及到Laplace方程的基本解,相对比较繁琐.本文受文献[5-6]的启发,利用单双层位势在尖角处的跳跃关系得到一种形式较为简单的边界积分方程,从而便于数值求解.然后再分别采用指数变换、周期变换和K ress变换对尖角区域进行处理,使双层位势在尖角处连续.最后求解带尖角区域声波散射问题的数值算例,对三种变换下的求解结果和收敛速度进行了比较分析,总结出在相同精度下周期变换在处理该问题时的收敛速度最快.

2 带尖角区域声波散射问题的边界积分方程

不妨考虑在均匀介质中传播的声波碰到一个无限长的柱体,设柱体截面D⊂R2,母线平行于z轴.设入射波是平面波

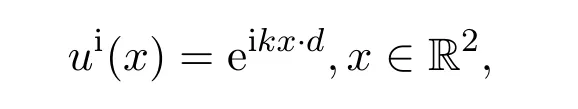
其中波数 k＞0,d为一单位向量,i表示虚数符号.入射波碰到柱体发生散射,记总体场为u=ui(x)+us(x),us(x)表示散射场,则散射问题归结为求u(x)∈C2(R2¯D)∩C(R2D),使其满足Helmholtz方程:

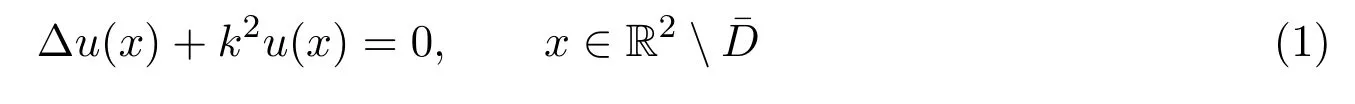
及其Dirichlet边界条件:

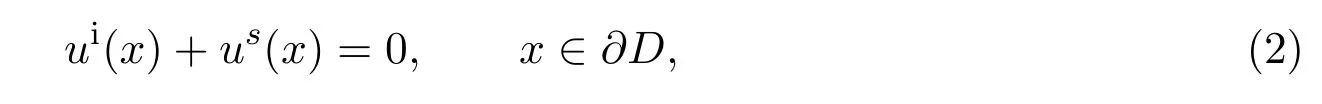
其中散射波us(x)满足Sommerfeld散射条件:

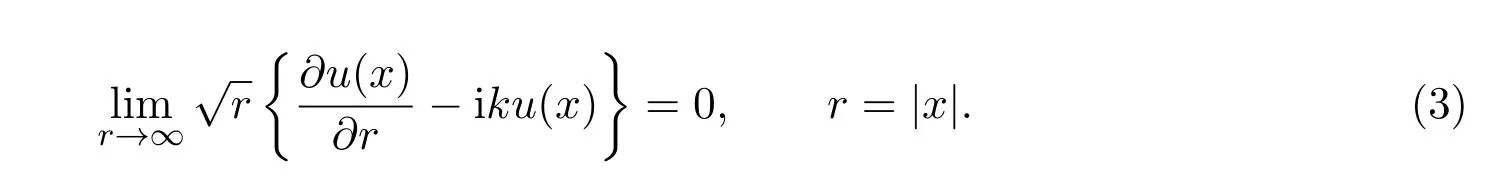
对于以上边值问题,不妨选取如下的单双层位势的混合形式来表示散射波us(x):

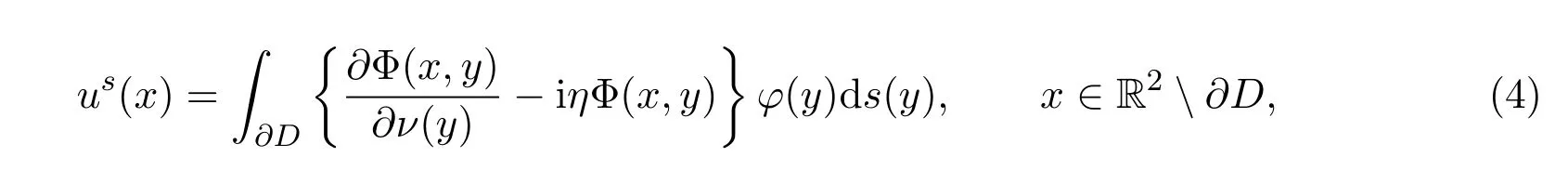
其中φ∈L2(∂D),η为常数,ν表示∂D的单位外法线方向,Φ(x,y)为Helmholtz方程的二维基本解,其形式为:

考虑散射域边界∂D上有一个尖点,不妨假设尖点在x=x0处,除尖点外∂D{x0}为C2类逐段光滑的,尖点处的内角记为γ0(0＜γ0＜2π).设由(4)式设定的散射波us(x)满足边界条件(2)式,再根据区域包含尖点时单双层位势的跳跃关系定理[4],有如下的边界积分方程:

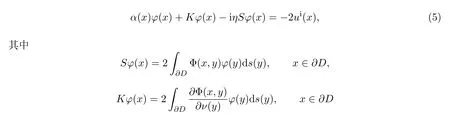
以及α(x)=γ(x)/π,γ(x)为区域边界在x点的内角.从而,在尖点x=x0处,α(x)=γ0/π;在其余点x̸=x0时,α(x)=1.

由Hankel函数的渐进性可得到由(4)式定义的散射波us(x)对应的远场模式为:

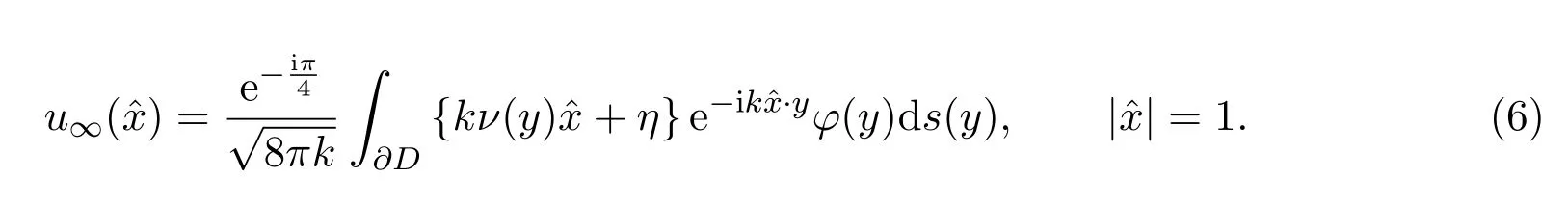
从边界积分方程中求出函数φ后,再代入(6)式计算出远场模式

3 三种变换

对于求解带尖角区域的声波散射问题,在其边界积分方程(5)之中,单层势的核函数在尖角处是连续的,双层势的核函数为基本解的方向导数,具体表示为如下形式:

显然,在尖角左右两端的边界外法向量ν(y)是不连续的,从而导致了双层位势的核函数在尖角处不连续.假设区域边界表示为:

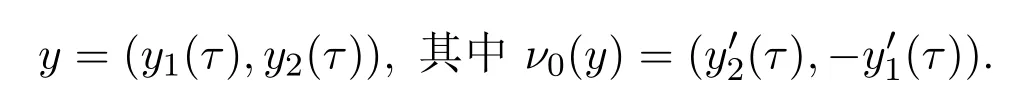
不妨采用参变量替换的方法,令τ=w(s),将现有变量τ替换为新参变量s,从而

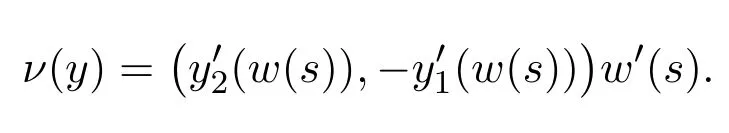
如果w(s)的选取能使得在尖角处w′(s)=0,这样就使得双层位势的核函数在尖角处连续且值为零.为此,有以下几种变换方法:

(1)指数变换:

4 离散化及奇异性处理

5 数值算例

例1 求解雨滴型区域的声波散射问题,其边界的参数表达式为:

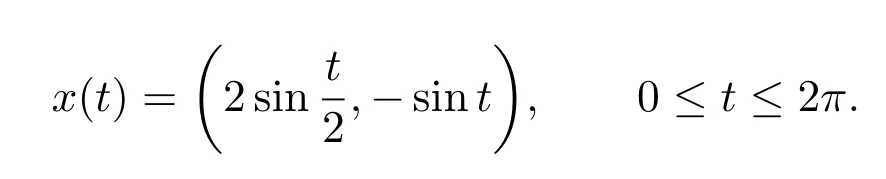
区域的图形如图1所示.

不妨取入射方向d=(1,0),波数为k=1.文献[4]中对该数值算例进行了求解,但是其处理方法和本文中的方法是不同的.以下给出本文应用指数变换、周期变换、K ress变换结合边界积分方程求解出的远场模式的计算结果.具体见表1-表5.

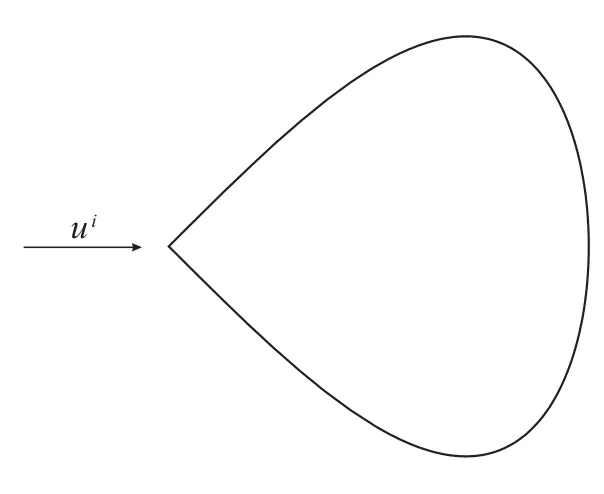
图1 雨滴型散射区域

表1 用指数变换求得的远场模式数值解

表2 用周期变换求得的远场模式数值解(p=2)

表3 用周期变换求得的远场模式数值解(p=8)

表4 用K ress变换求得的远场模式数值解(p=2)

从计算结果可以看出,用这三种变换方法来处理尖点区域声波散射问题都是可行的.其次,从收敛速度上来说,周期变换和K ress变换在p取值较大时,求解结果的收敛速度较快,因此可以通过调节p的值来调节算法的收敛速度.就求解结果前5位有效数字的收敛情况来看,在p都取2的情况下,周期变换在n=32时已经收敛,而K ress变换在n=128时还没有收敛,在p都取8的情况下,周期变换在n=16时已经收敛,K ress变换在n=32时才收敛.因此,在p取相同值时,周期变换的收敛速度更快.指数变换是固定的,其收敛速度和周期变换在p=2时基本相同,但该变换是无法调节收敛速度的.综上所述,周期变换的收敛速度可以调整,而且在几种变换中的收敛速度最快,因此周期变换是解决尖角区域的声波散射问题的最佳方法.该结果和文献[4]的结果相同,从而验证了该方法的有效性和可行性,但和文献[4]使用的方法相比本文建立的边界积分方程更加简单.

表5 用K ress变换求得的远场模式数值解(p=8)

[1]Colton D,K ress R.Integeral Equation M ethods in Scattering Theroy[M].New York:W iley-Interscience Publication,1983.

[2]K ress R.Linner Intergral Equation[M].New York:Springer-Verlag,1989.

[3]张梅东,王连堂.带尖角的障碍声波散射区域的反演[J].纯粹数学与应用数学,2009,25(3):610-616.

[4]王桃正,王连堂.基于周期变换求解带尖角区域的声波散射问题[J].纯粹数学与应用数学,2011,27(6):814-818.

[5]Colton D,K ress R.Inverse Acoustic and Electromagnetic Scattering Theroy[M].New York:Springer-Verlag, 1992.

[6]K ress R.A Nystrom method for boundary integral equations in domains with corners[J].Numer.Math., 1990,58:145-161.

Three num ericalm ethods based on solv ing the acoustic scattering p rob lem with a corner

Peng Zengjun

(Departm ent of M athem atics,Northwest University,X i′an 710127,China)

Using single and double-layer potentials′the jum p relation at sharp corner build a sim p le boundary integral equation.Three kinds ofm ethods which are exponential transform ation,periodic transform ation and K ress transform ation are used to process the sharp region.Num erical exam p le is given and the resu lts show that periodic transformation is best.

acoustic scattering,dom ains with corners,exponential transform ation,period transform ation, K ress transform ation

O178

A

1008-5513(2012)06-0819-07

2012-04-18.

陕西省教育厅基金(09JK 771).

彭增军(1987-),硕士生,研究方向:数学物理反问题.

2010 M SC:35A 40