基于动态规划的制导滑翔炸弹最优控制研究
2012-07-04林忠贤
雷 科, 林忠贤
(中国空空导弹研究院,河南 洛阳 471009)
0 引言
空中防区外精确打击已成为目前高技术战争的一种重要作战模式,并成为制约战争胜负的重要因素。在实施精确打击的弹药中,制导滑翔炸弹由于其低成本、精确打击能力及防区外发射等特点,受到各军事大国的普遍重视[1]。
制导滑翔炸弹没有动力,主要采用大升阻比气动外形,依靠投放高度势能和投放初速度动能来实现较远的滑翔距离。滑翔制导炸弹采用怎样的导引策略才能实现最远的滑翔距离,是一个具有现实意义的问题。
根据最优控制理论,制导滑翔炸弹最优滑翔距离问题应该属于多变量有约束的非线性系统最优化问题。目前对于多变量有约束的优化问题解法很多,适合于制导炸弹的方法有:梯度法、共轭梯度法、动态规划法、可行方向法、梯度投影法等[2]。
根据制导滑翔弹的特点采用动态规划法来进行寻优计算,它比常见的以最优升阻比方法获得远距离滑翔具有较好的效果。动态规划是一个发展成熟的理论,它与极大值原理一样被称为现代变分法,是处理控制变量存在有界闭集约束时,确定最优控制解的有效数学方法。它可以解决非线性多输入输出系统、时变系统的最优控制问题。从本质上讲,动态规划是一种非线性规划,其核心是贝尔曼的最优原理[3]。
1 制导滑翔炸弹滑翔问题分析
由于滑翔弹偏航控制通道主要消除航向制导误差,俯仰控制通道保证炸弹的飞行距离满足要求,末端主要对准目标,同时增大俯仰角,以所需的俯仰角命中目标。滑翔弹的性能优劣主要取决于垂直面的制导性能。而最优滑翔距离主要是通过俯仰通道的最优控制来实现的,因此,为了简化制导炸弹最优控制数学模型,本文只在垂直平面内对炸弹最优滑翔问题进行分析。
炸弹在滑翔过程中受重力、气动力合力作用。在不考虑侧滑情况下,制导滑翔炸弹在垂直平面内受力情况如图1所示。

图1 制导滑翔炸弹受力示意图Fig.1 The forces on the guided glide bomb
制导滑翔炸弹最远滑翔距离的要求还与末端着地角要求、制导精度要求、末速要求相互约束。
2 最优滑翔弹道数学模型
利用最优控制理论,将制导滑翔炸弹滑翔弹道的优化表述为一个非线性、时变、带有控制约束和终端约束的最优控制问题[4],其状态方程为
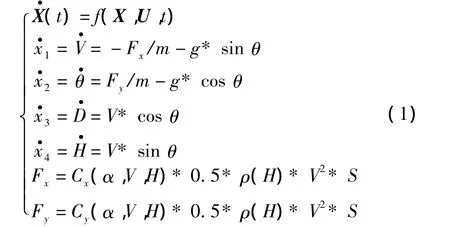
式中:X=(x1,x2,x3,x4)T为状态向量;U 为控制向量;t为时间(s);S为炸弹特征面积(m2);H为炸弹高度;m为炸弹质量(kg);V为炸弹速度(m/s);ρ(H)为空气密度(高度 H的函数)(kg/m3);θ为炸弹弹道倾角(rad);β为炸弹俯仰角(rad);α为炸弹攻角(rad);Fx为炸弹阻力(N);Fy为炸弹升力(N)。
根据动态规划原理,选取攻角为控制量,即

容许控制为
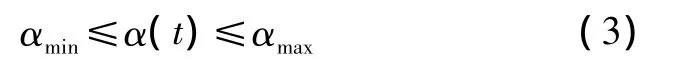
过程约束
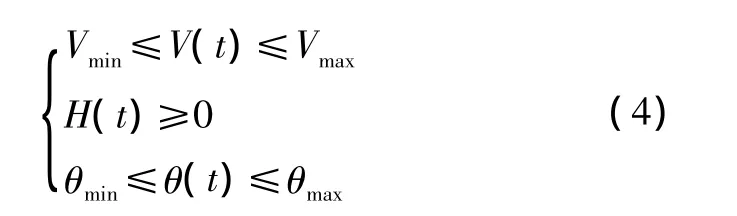
过程约束在程序中进行了限制,当超过过程约束时,该控制下的最优策略停止搜索。
终端约束为

制导炸弹滑翔距离作为性能指标,则性能指标函数为
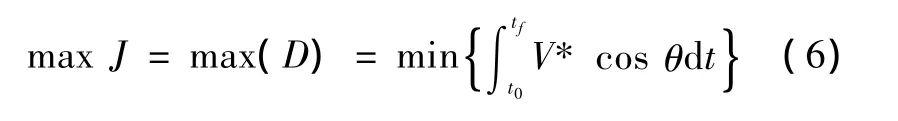
式中:tf为终端时间;t0为开始时间。
考虑到有约束终端求解比较困难,采用惩罚函数将终端约束以罚函数的形式放到性能指标函数中,有终端约束最优控制问题转化为无终端约束的最优控制问题[5],则性能指标函数为

根据最优控制原理,性能指标的极大值与极小值可以采用相同的哈密顿函数来进行求解[6],则最优滑翔弹道的哈密顿函数为
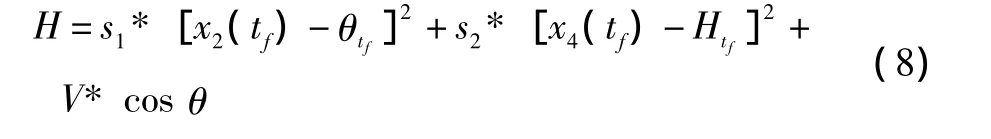
3 动态规划算法
动态规划的方法实质上是引进了最佳性原理,把一个多步最优化问题转换为多个一步最优问题。动态规划原理[7]:如果 u*(0),u*(1),u*(2),…,u*(N-1)是最优控制问题的一个最优控制序列,那么u*(1),u*(2),…,u*(N-1)一定也是一个最优序列,其初始状态是 X(1)=f1(X(0),u*(0))。
如果 u*(0)已求出,求 u*(1),u*(2),…,u*(N-1)的问题构成一个初始条件为X(1)的N-1步的最优控制问题,如果性能指标最小值记为(X(1)),这样由最优性原理有
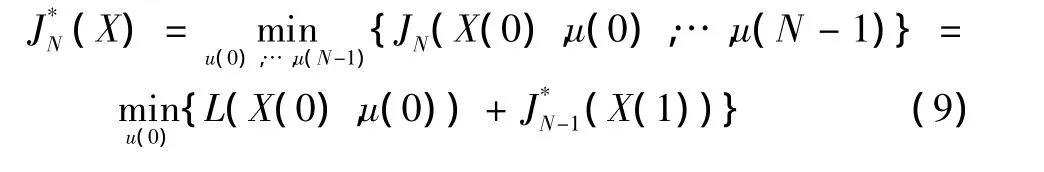
目标函数JN为
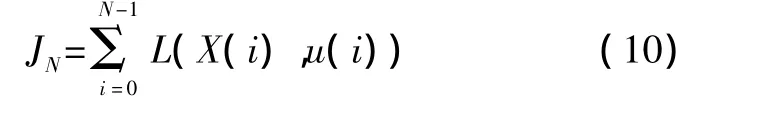
式中:N为由u*(0)到u*(N-1)的N步控制。从上述(X)到(X)之间的递推关系,可以把N步控制的问题转化为N个一步控制问题。
对终端有约束的最优控制问题,动态规划常规的方法是由终端状态逆向进行搜索。制导炸弹如果也采用这种方法进行求解,到最后同样要回到初始状态的特定值的约束,相当于顺序求解法的末端约束,而且编程较为困难。因此采用动态规划法的顺序求解法进行弹道的求解,较为直观简单,也比较适合于本文问题的求解。但由于末端对着地角和末速有约束限制,直接用顺序求解法无法求解,因此引入拐弯时间进入动态规划,在拐弯时间Tturn之前,每阶段的性能指标函数采用J1的形式,即不考虑末端约束,以最远距离为唯一性能指标。拐弯时间之后,性能指标变为增加末端约束的最终J2指标形式,即
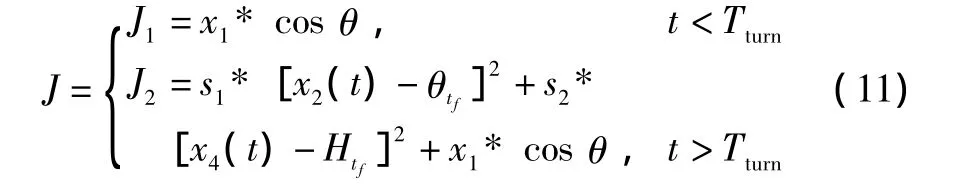
其中:s1、s2为惩罚因子。
根据动态规划原理,结合滑翔炸弹的运动特点,采用的动态规划法如图2所示。

图2 动态规划算法示意图Fig.2 Diagram of the dynamic programming algorithm
以时间为单位将制导炸弹划分为N个阶段,每个阶段根据攻角的范围,确定I个攻角策略。具体的计算步骤如下。
1)设定转弯时间的取值范围,Tturn∈[min TR,max TR]。
2)设定转弯时间Tturn=min TR。
3)设定炸弹飞行仿真时间t=0,如果t<Tturn,则性能指标按照J1的形式计算,否则性能指标按照J2进行,即
4)根据初始状态,计算第1阶段I个策略下的弹道运动方程,将状态数据,,,,…和性能指标,,,,…,记录下来,作为第2个策略计算的初始值。
8)采用4)相同的计算方法计算3,4,…,n阶段的最优控制,当所有策略下都不满足过程约束时停止搜索,搜索所有性能指标J,其中最大的J指标即为最远射程。最远射程对应的即为最优攻角序列。
9)Tturn=Tturn+1,如果 Tturn<max TR,转到2)重新开始计算。如果Tturn>max TR,结束所有计算,对应所有转弯时间下的最优性能指标J为最优控制序列。
由于简化的制导滑翔弹数学模型变量较少,较为适合采用动态规划算法。当然每个阶段时间的划分不宜太短。如果太短,则总阶段太长,会导致数据记录量太大,总的计算时间太长[8]。但如果每阶段的时间太长,则所计算的精度不够,不能计算出最优攻角序列。经过反复仿真分析发现,本文的仿真步长选取1 s可以获得较好的效果。
4 仿真结果分析
为了验证以上动态规划法的有效性并与最优升阻比进行比较,本文根据某制导炸弹的气动数据进行仿真验证。取初始状态X(t0)=(190 0 0 10000)T,过程和末端速度约束范围[Vmin,Vmax]=[160,300],单位为 m/s。过程和末端角度约束范围[θmin,θmax]=[-80,30],单位为(°)。高度和射程单位为 m。拐弯时间根据初步估算在Tturn=[250,500]内取值较为合理,单位为s。当满足条件|x4-Htf|<ε,或过程状态超过约束时停止迭代。其中ε=10[9]。动态规划求解的最优滑翔弹道的结果如表1所示。

表1 动态规划计算结果Table 1 The result of the dynamic programming calculation
根据表1的计算结果,可以看出,当转弯时间为360 s的时候,在满足末端约束的条件下,射程达到最大的66 km。随着拐弯时间的不断后移,其末端速度和弹着角逐渐减小,到371 s时,已经不能满足末端约束的要求。
在文献[10]中对最优滑翔的结论为:导弹在滑翔过程中采用最大升阻比进行下滑,基本上就可以得到最大滑翔距离,因此,采用本方法与最大升阻比方法对10 km高度下,相同飞行速度在相同的末制导条件下计算结果进行比较,其末端数据如表2所示。

表2 动态规划法和升阻比法的末端数据对比Table 2 The terminal data of dynamic programming algorithm and lift-drag ratio algorithm
从表2可以看出,在10 km高度,采用动态规划法计算的最优射程比最优攻角制导增加6 km以上,同时末端着地角可达到-45°,但末速比最优升阻比减小了70 m/s,末端性能要优于最优升阻比制导。
动态规划与最大升阻比的弹道曲线如图3所示。

图3 动态规划与最优升阻比弹道对比图Fig.3 The trajectory of the dynamic programming algorithm and optimization lift-drag ratio algorithm
从图3可以看出,从投放开始后,采用动态规划法就比最大升阻比法滑翔的高度要高,同时考虑到末速要比最大升阻比法低70 m/s,说明这种方法依靠速度损失增加了射程。同时,动态规划法的拐弯高度和最优升阻比相当,即在增加射程的同时保证了末端姿态调整的时间,从而保证着地角末端约束。
图4为采用动态规划计算的过载曲线,该过载保证了导弹在整个弹道过程中滑翔距离最远,在末端过载迅速减小调整姿态,保证着地角满足着地角约束。
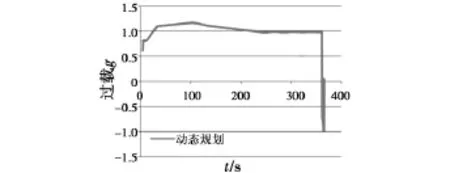
图4 动态规划计算的过载曲线Fig.4 The overlade curve of the dynamic programming algorithm
5 结束语
本文通过改进的动态规划法对最优滑翔距离制导问题进行了研究,算法简单。基于某滑翔弹实际气动参数进行仿真证明其效果良好,该算法比最优升阻比制导方法投放距离远。研究结果对于分析制导炸弹飞行控制系统性能、滑翔飞行特性及进行滑翔飞行方案制定、控制系统设计具有重要参考价值。
本文研究的结果,对亚音速正常式气动布局滑翔弹制导初步设计、弹道规划和性能初步分析使用具有实际应用意义。
[1]侯明善.防区外投放制导炸弹滑翔段垂直面最优制导[J].兵工学报,2007(5):12-16.
[2]黄国强,南英.二级入轨空天飞机上升轨迹优化[J].宇航学报,2010(3):641-647.
[3]王晓陵.最优化方法与最优控制[M].哈尔滨:哈尔滨工程大学出版社,2007.
[4]牛蕴轩.基于均匀设计的制导炸弹运动参数相应面建模[J].火力与指挥控制,2011,36(7):171-173.
[5]童季贤.最优控制的数学方法及应用[M].成都:西南交通大学出版社,1994.
[6]孙明玮,彭南楠,杨明.导弹最优滑翔弹道的设计及存在的问题[J].飞行力学,2006,24(1):26-29.
[7]李国勇.最优控制理论及参数优化[M].北京:国防工业出版社,2005.
[8]南英.航天器轨迹优化的通用数值算法[J].飞行力学,1996,14(3):20-26.
[9]张敏,戴通伟.战机最速角度机动攻击导引指令生成算法[J].火力与指挥控制,2010(11):24-27.
[10]VINH N X.Optimal trajectories in atmospheric flight[M].Amsterdam:Elsevier Scientific Publishing company,1981.
