基于协商对策的多平台目标跟踪冲突消解

蔺 敏， 冯 星， 陈 谋， 姜长生

(1.南京航空航天大学自动化学院，南京 210016;2.光电控制技术重点实验室，河南洛阳 471009)

0 引言

目标跟踪在军事及民用的诸多领域均得到广泛应用，随着科学技术的飞速发展，各种雷达、红外、激光、声纳等目标跟踪系统相继取得迅速发展并且日趋完善［1］。现代作战过程中，目标机动性增强，数量增多，单平台跟踪可能因为自身品质、性能及噪声的影响，采集到的信息往往不完善，或有较大的不确定性，导致获得的目标航迹时断时续甚至丢失目标。显然，基于单平台的目标跟踪已经不能满足跟踪精度的要求，于是人们开始研究基于多平台的目标定位与跟踪的方法及体系。当然，基于多平台的目标定位与跟踪系统并不是一般意义上多个平台的简单集合，而是在总体性能与功能上能够协调工作的传感器平台。

空中目标跟踪过程中，多平台具有单平台所无法获得的信息搜集、处理、战场态势掌握与控制能力［2］。基于多平台的空中单目标跟踪，可以直接根据平台与目标间的距离以及平台可探测范围内的跟踪精度来确定平台的优先权;而当多平台跟踪空中多机动目标时，问题就会变得复杂。首先，目标与跟踪平台都是运动的，为了保证高精度跟踪，在整个跟踪过程中就需要解决平台的实时切换问题，切换时分配给平台的跟踪任务应考虑平台的执行能力以及对目标的跟踪精度。也就是说，要既能够保证多平台协同下的精确跟踪，又不浪费平台资源，此时冲突就可能产生。例如，在某一时刻，多个平台能够同时探测同一目标时将产生任务分配冲突，或者某一平台同时能够跟踪多个目标时出现平台资源冲突。基于多平台空中机动目标跟踪，目的是能够提高对目标的跟踪精度，而且要比单平台表现出明显的优越性，关键是因为多平台间可以存在相互合作。既然可以合作，也就意味着冲突问题可以进行协商，能够取得协商对策解［3］。因此，可以考虑通过协商来解决各类冲突问题。文献［3］针对卫星任务规划过程中预处理阶段的目标冲突特点提出了基于协商对策的冲突消解方法;文献［4］也以水库兴利调度决策的多目标性和群决策特点为背景研究了基于协商对策的多目标群决策模型，并对调度方案进行优化决策，最终得到满意方案，为水库实际运行提供依据等。本文对基于多平台的空中目标跟踪过程中产生的冲突问题进行研究，从提高跟踪精度以及合理利用平台资源的角度出发，研究了基于协商对策的多平台跟踪机动目标的冲突消解方法，并通过仿真验证该方法的有效性。

1 问题描述

1.1 目标跟踪原理概述

目标跟踪是基于具有不确定性测量的传感器数据，对来自未知目标的运动学特征做出估计的过程［5］。机动目标跟踪的本质是随机动态混合系统中的状态估计问题，其难点在于每一时刻运动模式的高度不确定性。在实际问题中，系统状态往往呈现出非线性、非高斯等特点［6］。目标跟踪技术在国防上占据着极其重要的地位，例如反弹道导弹的防御、控制预警、地对空、舰对空、空对空的超视距目标探测、跟踪、攻击、战区监视、精确制导与打击、低空突防等［7］。军事上，随着光电对抗、电子对抗技术的发展，目标的机动性能不断改善，被探测目标的不确定性变得更加复杂。典型的目标跟踪系统原理如图1所示［8］。基于多平台的机动目标跟踪系统，要求在能够合理利用平台资源同时，适应多个目标的机动变化，实时做出正确的相关决策，在确保完全跟踪的前提下，提高对目标的跟踪精度。

图1中:X表示状态向量;Z为量测量;V是量测噪声;d表示残差向量。由量测Z和测量预测HX^(k+1/k)构成残差向量d，再根据d的变化进行机动检测或辨识，按照某准则或逻辑调整滤波增益与协方差矩阵，或者实时辨识出目标的机动特性，最后由滤波算法得到目标的状态估计值和预测值，从而完成机动目标跟踪。

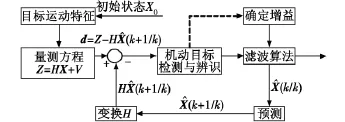
图1 机动目标跟踪系统基本原理Fig.1 The basic principles of maneuvering target tracking system

日常生活中，人们常常把协商作为冲突消解和信息交换的一种重要方式，协商机制主要起协调作用，以达到缓和直至解决矛盾的目的。在多平台协同合作的空中目标跟踪系统中，对会出现的冲突问题进行协商，通过搜索动态问题空间找到一个折中的解来协调存在相互制约的矛盾，解决因各种原因(资源有限、目标差异等)产生的冲突，以达到冲突消解的目的。而对策论［9］作为一种数学工具，处理各类带有矛盾因素的模型，已广泛应用于讨论各类存在着冲突、矛盾、合作等问题中。作为对策论分支的协商对策理论考虑的是一类非零和、非结盟的合作对策问题。“零和效应”的意思是:实力相当的双方在谈判时做出大体相当的让步，方可取得结果，亦即每一方所得与所失的代数和大致为零，协商便可成功。然而，社会发展的历程越来越走向“非零和”，也就是所谓的双赢。非零和问题使合作成为可能，而合作必然至少存在一个比非合作对策“更好”的解［3］。因此，基于协商对策的冲突消解方法的提出是合理的，能够使问题的解决向有利的方向发展。

1.2 基于多平台空中单目标跟踪冲突问题

若存在多个平台，且各平台在任意时刻都可被使用。对于空中单机动目标，各平台的测量值彼此间相互独立。此时单目标跟踪是指多平台协同跟踪同一个目标。平台间需要交换测量数据，以确定目标的位置和运动轨迹，预测目标的运动方向。在某一时刻，并非所有的平台都可以探测到目标，也并不需要所有平台都同时参与跟踪，即使参与了目标跟踪，每个平台对运动目标状态估计的贡献大小也不尽相同，因此为了合理充分地利用平台资源，有必要对参与跟踪的平台进行初始化选择，然后进行数据融合以达到高精度目标跟踪的目的。整个过程中，为了避免平台资源浪费，可以对能够探测目标的平台设置定时器实行“轮休”制，实现对目标的精确跟踪。基于多平台的空中单目标跟踪模型如图2所示。其中:T为目标;P1、P2、P3分别为跟踪平台，一般地，距离目标越近，与目标间夹角越大，跟踪精度越高。P1与T之间为虚线，表示此时P1可以暂时“休息”，由P2和P3对目标进行跟踪就能保证跟踪精度，同时降低了平台数量太多所造成的信息融合的复杂度，即可能某一时刻并不需要所有平台都对目标进行跟踪。基于多平台的单目标跟踪中存在的冲突问题相对比较简单，可以通过基本的数据融合算法加以解决，本文不作重点研究。

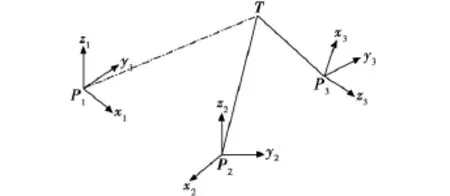
图2 基于多平台单目标跟踪模型Fig.2 Single-target tracking model based on multi-platform

1.3 基于多平台空中多目标跟踪冲突问题

随着目标机动性提高以及敌机突防密度和批次的增加，单目标定位跟踪已不能满足现代战争的需要，于是多目标跟踪已逐步成为当前的研究热点。对于多目标跟踪，由于平台间协同任务的并发性，执行过程中可能出现多个平台能够同时跟踪某个目标，或者某个平台可以同时探测多个目标，此时，平台选择与任务分配将会出现冲突，而冲突消解的目的是既能提高跟踪精度，又能合理利用平台资源，即尽可能使目标分配的均匀度较高，目标任务的分配最好不要过于集中，应当能够充分发挥每个平台的作用［10］。进行分配时希望，每一目标最多只分给一个平台，而每个平台可以同时跟踪多个目标，应该尽量避免重复跟踪，这一过程中就需要体现出冲突消解。如果分配给某一平台的目标任务已经达到其跟踪能力极限，则在进一步分配时，可以暂时性删除该平台，将剩余的平台与目标再进行分配。基于多平台多机动目标跟踪基本原理如图3所示。

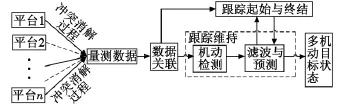
图3 基于多平台的多机动目标跟踪基本原理Fig.3 The basic principles of multi-target tracking based on multi-platform

2 基于协商对策的冲突消解方法

对于m个平台(包括预警机平台、战斗机平台和地面雷达站)协同跟踪空中n个机动目标(一般地，n≥m);协商过程中，需要同时达到跟踪精度与分配均匀度较高两个目标。很显然，当所有平台协同探测同一目标时，精度可能达到最高，而分配均匀度最高则要求平台利用率高的同时对每个目标都能实时跟踪，避免遗漏。二者之间存在的冲突，可以通过双方协商来解决。

冲突问题主要体现在任务分配过程中:根据平台与目标的初始化信息，首先判断各个平台能同时探测哪几个目标，在提高跟踪精度的前提下，难免出现这样的问题，某一时刻，某个平台可能同时对多个目标的跟踪精度都是最高，而当前的目标个数却超出了该平台的执行能力，所以，冲突之一，存在对目标的取舍。然而，对于被优先权最高的平台“淘汰”掉的目标，该如何分配来保证跟踪精度，是另一需要解决的冲突。基于多平台联合跟踪多个目标的过程中，不能保证平台对每个目标的跟踪精度都达到最高，而是通过冲突消解提高联合跟踪的整体精度。方便起见，对跟踪误差取绝对值，则跟踪精度和即误差绝对值之和，表示冲突消解后的目标跟踪精度，误差越小，则跟踪精度越大，跟踪效果越好。整个过程中，通俗来讲，就是考虑供需分配以及迫切程度，在顾全大局的前提下，进行协商，完成任务的全面分配，实现冲突消解。

假设:对于平台 Pi(i=1，2，…，m)和目标 Tj(j=1，2，…，n)，得到最终任务分配矩阵 R［i，j］，rij=1 表示平台Pi将选目标Tj为跟踪目标;rij=0表示平台Pi将不选目标Tj为跟踪目标。Nmax［i］表示第 i个平台最多可探测目标个数，即平台Pi的跟踪能力;A［i］为平台i的跟踪误差绝对值，L［i］表示平台i可探测距离。假设A［i］按照从小到大，即精度从高到低的顺序排列。需要说明的是，实际场景中，平台的跟踪精度会随着探测距离的变化而发生变化。此处，仅为了验证冲突消解方法的有效性，假设同一平台对不同目标的跟踪精度相等且为固定值。算法流程如图4所示。

算法描述如下:

1)令i=1，找出平台Pi可以探测的目标Tj，即根据平台分类，形成的初始矩阵为 Xm×n，其中，xij=，则X中第j列“1”的个数k表示目标Tj可被k个平台同时跟踪;i++;

2)若 i＞ m，令 j=1，对于目标 Tj，若 k=1，则R［i，j］=1，并标记第 j位;j++;

3)若 k≥2，即第 j列未被标记，对于平台 i，若xij=1，找出相应的所有第j列中第(i+1～m)行值为1的元素，按从小到大的顺序，取误差值最大时对应的平台 i暂存在 Ttemp［i，j］中;

4)在不超出平台i跟踪能力的前提下，以提高跟踪精度为原则，把Ttemp［i，j］中各元素从大到小排列，可被跟踪误差最大平台探测到的目标优先分配给平台i，并将第 j列标记;

5)若超出平台i的跟踪能力，则在能够探测的条件下，把目标分配给次优精度的平台;i++;若i＜m，转入4);

6)实现目标平台的全面分配，得出分配矩阵R［i，j］，计算跟踪精度之和 SSA，即冲突消解后的跟踪精度，使其尽量小，即求

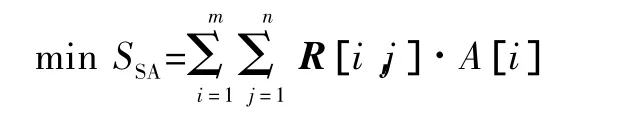
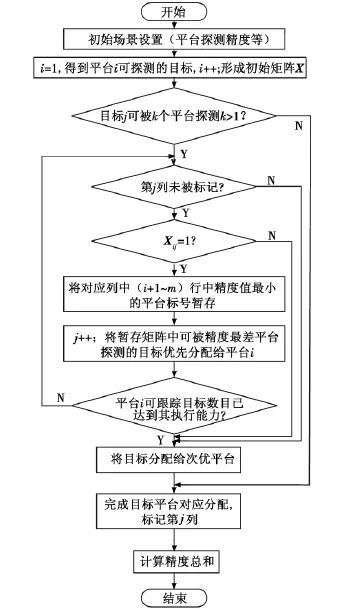
图4 基于协商对策冲突消解流程图Fig.4 The flow chart for conflict resolution based on bargaining games

3 实验仿真

3.1 仿真条件及环境

仿真时，假设有3个跟踪平台，包括地面雷达站和空中平台，有5个目标分成3个编队飞行。假设平台1为地面雷达站;平台2在X方向上做匀速直线运动;平台3在X、Y方向上均做匀速直线运动;各自探测距离分别为200 km、400 km和100 km，跟踪误差分别为0.05 km、0.1 km 和 0.2 km。目标 1、2 先在 X、Y 方向上做匀速直线运动，一段时间后在Y方向上产生加速度，变为抛物线运动;目标3先在Y方向上做匀速直线运动，某时刻后产生X方向的加速度;目标4、5一直做匀速直线运动。平台与目标运动轨迹在XOY平面上的投影如图5所示。

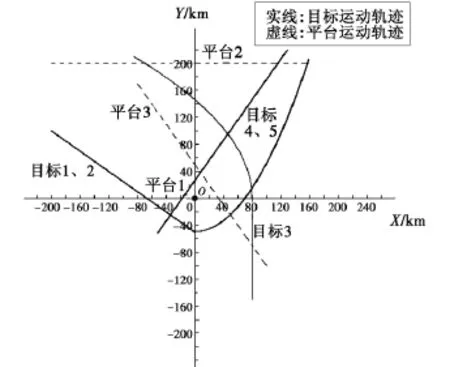
图5 平台与目标运动轨迹Fig.5 The trajectory of platforms and targets

3.2 仿真结果及分析

仿真结果如图6所示。

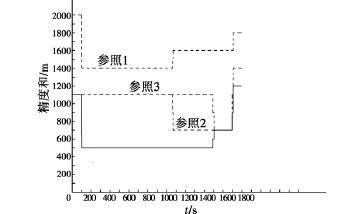
图6 基于协商对策冲突消解及参照任务分配下的跟踪精度之和曲线Fig.6 The tracking accuracy-amount curve of conflict resolution based on bargaining games and other reference allocation

对于多平台能够同时探测多目标的情况，若以平台为基准，尽量满足各平台跟踪能力，从跟踪误差最大(最小)的平台开始分配，对可探测目标跟踪，其跟踪精度和的曲线如参照1(参照2)所示;若以目标为基准，任意选择可探测的平台对其跟踪，跟踪精度和的曲线如参照3所示。由于仿真中假设同一平台对不同目标的跟踪精度相同，使得精度曲线的变化幅度不是很明显。但在同一假设条件下，与未考虑冲突情况的随机任务分配(即参照1、2、3)结果相比，基于协商对策进行冲突消解后的跟踪精度和较小，即跟踪精度有所提高。

4 结束语

本文通过分析多平台多机动目标跟踪过程中出现的冲突问题，参考了解决各类冲突问题较为成熟的相关理论知识，建立了基于协商对策的冲突消解流程，并仿真验证了该方法的可行性，实现了对目标的全面跟踪，通过与随机平台任务分配时的跟踪精度和比较，基于协商方法消解冲突后的任务分配，有效地提高了对空中多机动目标的跟踪精度。然而，要使仿真场景更合理，应该考虑平台与目标间距离对跟踪精度的影响，实现冲突消解，将成为下一步需要解决的问题。

［1］王亚利，林家骏.基于粒子滤波的机动目标跟踪［J］.计算机工程与应用，2007，43(34):61-64，80.

［2］王栋.基于数据融合的机载多传感器目标识别［D］.上海:上海交通大学，2010.

［3］祝汉江，黄维.基于协商对策的卫星任务规划冲突消解［J］.计算机仿真，2008，25(10):86-89.

［4］朱小凯，贾东权.基于协商对策的多目标群决策模型及其在白石水库调度中的应用［J］.水利水电技术，2010(2):65-67，79.

［5］刘国成，王永骥.一种基于改进粒子滤波的多目标跟踪算法［J］.控制与决策，2009，24(2):317-320.

［6］李景熹，王树宗，王航宇，等.基于多模型和辅助粒子滤波的机动目标跟踪算法研究［J］.武汉理工大学学报:交通科学与工程版，2007，31(4):703-706.

［7］杨廷梧，刘上乾.基于多传感器的机动目标跟踪与融合技术综述［J］.飞行试验，2004，20(2):2-7.

［8］陈俊丰.基于粒子滤波的机动目标跟踪算法研究［D］.杭州:浙江大学，2010.

［9］LO C Y，WU C F.The survey and expansion on quantitative methods to conflict resolution［C］//Proceedings of the Third International Conference on Information Technology and Application，2005(2):268-271.

［10］高文正，丁全心.多机协同攻击中的目标分配研究［J］.电光与控制，2003，10(4):10-15.