短路脱扣器特性研究

邓为 涂煜 金雪丰

（中国船舶重工集团第七一二研究所，武汉 430064）

0 引言

短路脱扣器是直流快速断路器对线路进行短路保护的执行部件。直流快速断路器是一种限流型断路器，其对短路电流的限制作用体现在短路脱扣器上。短路发生时，短路电流还没有上升至预期短路电流，短路脱扣器就动作使断路器解扣分断。如图1所示，左上部分坐标系中曲线1为短路发生时预期短路电流波形，曲线2为断路器动作时的实际电流波形。短路电流上升至脱扣器整定值时，脱扣器开始动作，断路器解扣，动静触头分离，触头间产生电弧，断口恢复电压从零开始上升，电弧从触头进入灭弧栅片，弧压迅速上升。当电源提供的能量不足以维持电弧持续燃烧所需能量时，电弧电流不断下降，直至电流为零时，电弧熄灭，断口电压与电源电压相同，线路被切断。

脱扣器动作时间越短，断路器分断越快，脱扣器动作特性对决定了断路器的快速性。扣器的铁磁吸力和碟簧反力都是非线性的，很难通过直接计算来分析脱扣器的动态特性。传统脱扣器设计需要经过多轮实验验证，不断改进，费时费力。仿真设计和数学处理软件为脱扣器的动态特性定量计算提供了可能，计算结果可以为设计或者改进设计提供依据，减少实验轮次。

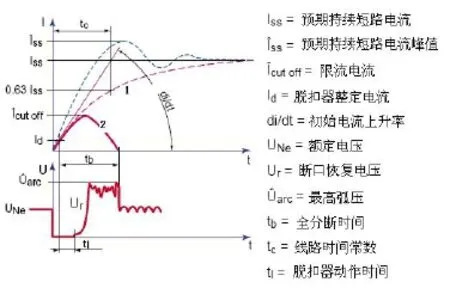
图1 直流快速开关短路分断示意图[1]

1 短路脱扣器静态分析计算

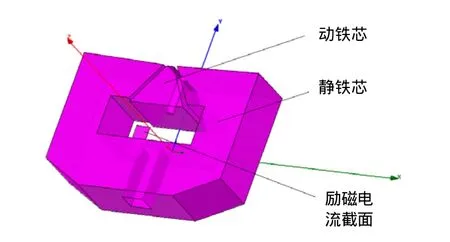
图2 短路脱扣器仿真模型

利用 Ansoft对短路脱扣器进行三维建模仿真，仿真模型如图2所示，包括3个部分：静铁芯、动铁芯和激磁部分。对于脱扣器其它部分，由于对磁路没有影响，模型中不予考虑。

进行网格剖分之后的模型如图3所示。网格剖分太粗会导致计算精度差，但过细又会带来过大的运算量。实际剖分应选择合适的大小，计算精度和计算量二者兼顾[3,4]。

图3 仿真模型网格剖分

电流为4000 A时，用Ansoft软件计算不同气隙下的脱扣器铁芯吸力[5]，根据计算的数据点在 Matlab中绘制的铁芯吸力随气隙变化曲线如图4所示。随着气隙长度的减小，吸力增加越来越快。实际短路发生时，短路电流还会不断上升，吸力会进一步增加。

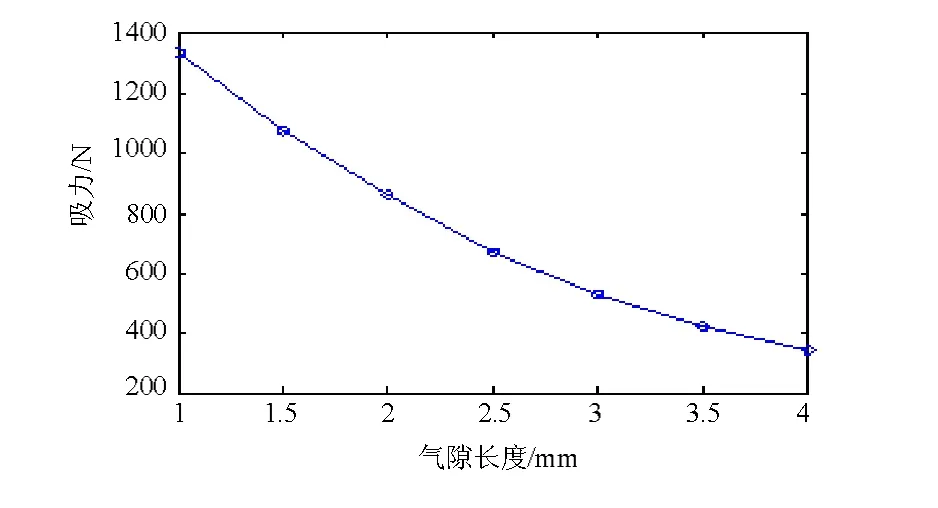
图4 铁芯吸力随气隙变化曲线

对数据点进行最小二乘拟合，拟合出的二阶多项式为

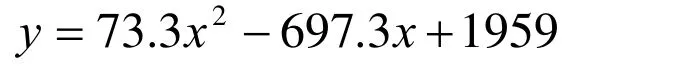
其中x为气隙长度，y为铁芯吸力。

碟簧力与形变之间具有非线性特性，为了得到较准确的反力特性，需要对碟簧进行实验测试，将测试出的数据进行拟合，得到反映碟簧特性的数学表达式。对短路脱扣器利用弹簧测力机进行测试，碟簧总的初始形变为4.5 mm, 将测力机可动端行程换算为碟簧总形变，得到碟簧总形变量与碟簧力的关系曲线（补充总形变为零的点）如图5所示。

对数据点进行最小二乘拟合，拟合出的二阶多项式为

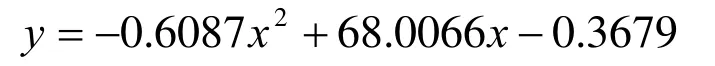
其中x为碟簧总的形变量，y为碟簧力。

图5 碟簧总形变量与碟簧力关系曲线

在试验室对脱扣器进行整定试验，整定回路利用直流发电机作为电源，该电机输出电压为定值，通过改变励磁电阻得到变化的电流。实验时先将脱扣器指示器调整到合适的位置，不断调节整定回路电流，脱扣器刚好能动作（脱扣器不动作时的回路电流与紧接着的下一次实验动作时的回路电流相差10%以内）的电流即为整定电流。将脱扣器刻度换算为碟簧压缩量，整定电流与碟簧压缩量对应关系如表1所示：

表1 碟簧压缩量对应的整定电流

利用碟簧力特性拟合公式得到不同碟簧压缩量对应的碟簧力，根据ansoft仿真计算得到的电流为2800 A时的电磁吸力，以及电流与力的关系（在铁芯未饱和时电磁吸力与电流的平方成正比）得到不同整定电流对应的电磁吸力，如表 2所示。

表2 整定电流对应的电磁吸力

从表中可以看出，两种力的偏差在10%以内，考虑测量和计算误差，两种力的偏差在可接受范围之内。

2 脱扣器动态特性数值计算及实验对比

脱扣器动铁芯部分的运动遵循达朗贝尔方程[2]：

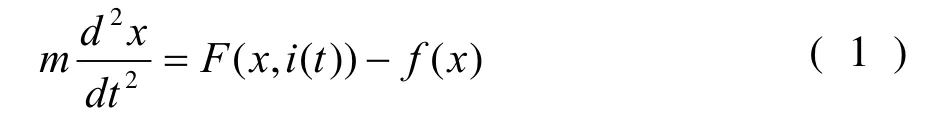
其中F(x,i)为电磁吸力，f(x)为碟簧反力，动铁芯部分重力忽略不计，机构摩擦同样忽略不计，m为运动部分等效质量，i(t)为短路电流。短路电流与预期短路电流峰值IP和线路时间常数τ有关，其表达式为

当F ( x ,i(t))≤ f(x)时，脱扣器动铁心的速度 v ( t)及加速度 a ( t)都为0，即有下式成立；

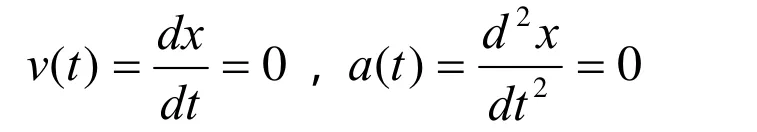
当脱扣器铁心未饱和时，相同气隙长度下，电磁力与电流的平方成正比[5]。因此电磁力可以按照下式计算：

根据文章前面得到的碟簧与形变的拟合曲线，碟簧反力按下式计算，式中x为动铁心位移，l0为碟簧预压缩量：

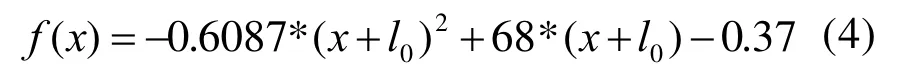
采用表达式（1）到（4），就可以在 Matlab中对脱扣器动态特性进行数值计算。计算前，首先对以下变量赋初值：气隙长度d0，位移x0，碟簧预压缩量 l0，碟簧预压力 f0，运动部件的质量m。

短路电流到来时，判断不同时刻的电磁吸力是否到达碟簧预压力，如果没有，继续计算下一时刻电磁吸力，直到电磁吸力等于碟簧预压力（实际判断时以是否大于或等于作为判据）。这一阶段动铁芯位移为零，速度为零，加速度为零。

当电磁吸力开始超过碟簧预压力时，利用运动定律计算不同时刻的加速度，速度，位移，利用前一时刻的计算结果计算下一时刻的加速度、速度、位移。当位移达到额定位移xe时，计算结束。

取IP=80000 A，τ=32 ms，l0=5 mm，设定行程8 mm，运动部件质量m=1 kg。计算短路电流及动铁心运动参数。根据计算结果绘制的短路电流波形如图6所示，动铁芯部分位移随时间变化曲线，加速度随时间变化曲线以及速度随时间变化曲线如图7所示。开始阶段，由于短路电流较小，电磁吸力也较小，动铁芯部分速度、加速度、位移均为零。当短路电流增加到一定值（与实际整定值相对应）时，动铁芯部分加速度不断增加，速度也不断增加，位移不断增加。这里虽然设定行程为 8 mm，实际过程中，动铁芯走完空行程即开始撞击拨叉杆使断路器解扣。动铁芯部分走完4 mm时断路器实际上已完成解扣。脱扣器的动作时间以动铁心移动4 mm为结束。这里计算的脱扣器动作时间约为4 ms，实际轨道交通对脱扣器动作时间要求为5 ms以内，该脱扣器满足动作时间要求。

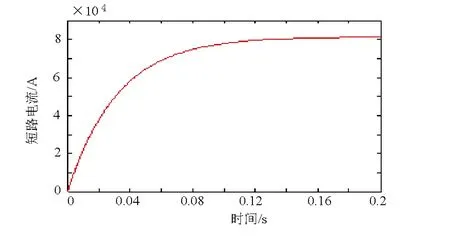
图6 预期短路电流仿真波形

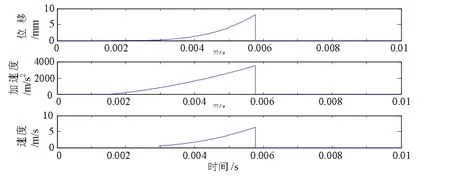
图7 脱扣器动作特性曲线

在断流容量试验室对断路器进行分断实验。通过调节线路参数，得到所需的时间常数和预期短路电流。分断波形如图8所示，脱扣器动作时间从电流到达整定值开始计时，以断口电压上升起点作为计时终点，从波形图测得的脱扣器动作时间约为4.2 ms，与仿真计算结果基本吻合。

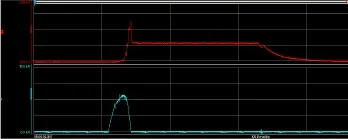
图8 开关分断实验波形

4 结论

通过 Ansoft软件计算出脱扣器在指定电流下不同气隙的电磁力，然后对电磁力与气隙的关系进行拟合，得到电磁力与气隙间的近似函数关系。脱扣器铁心未饱和时，电磁力与电流平方成正比，因此不同电流下的电磁力也可以通过拟合函数计算出来。通过电磁力与碟簧的拟合函数以及运动函数，可以在Matlab中对脱扣器动作时间进行计算。采用拟合函数的方法计算脱扣器的动作时间，方法简单易行，计算精度也满足工程要求，其关键在于拟合函数要有足够精度。在进行短路脱扣器的设计时，通过仿真软件预估脱扣器的动作时间，可以减少脱扣器的试验轮次，提高设计效率。

[1]UR26 36 40 46. 直流快速断路器产品样本, 瑞士赛雪龙公司.

[2]张冠生 电器学理论基础. 机械工业出版社

[3]俞国勇. 塑壳断路器瞬时脱扣器动静特性仿真及优化. 电工电气, 2009(1).

[4]向洪岗. 应用有限元方法分析塑壳断路器磁脱扣器的动作特性. 西安交通大学学报, 2005(8).

[5]金晓明. 基于脱扣线圈电流的断路器机械状态预测算法研究. 高压电器, 2010(4).