基于Backstepping的船舶航向自适应滑模控制
2012-07-03王林陈楠高嵬
王林 陈楠 高嵬
(1. 海军驻武汉701所军事代表室,武汉 430064;2. 91206部队,山东青岛 266071;3. 海军工程大学电气与信息工程学院,武汉 430033)
0 引言
由于船舶的动态特性或外界条件不断地变化,使得船舶运动表现出非线性、不确定性、大滞后等复杂的动态特性,从而船舶航向控制的数学模型与扰动模型具有明显的不确定性,而以确定数学模型为基础的PID舵的设计就无法实现。近年来,非线性控制理论的发展为复杂系统的控制问题提出了新的解决方法。其中自适应逆推算法(backstepping)[1-3]和具有强鲁棒性的滑模控制[4-6]得到了较快的发展,将backstepping算法与滑模控制[7-8]的结合集成了二者的优点,拓宽了滑模控制的应用范围,并且提高滑模控制的控制品质。
本文针对 Norrbin非线性数学模型,在考虑外界扰动的情况下,将自适应backstepping算法与滑模控制相结合,提出了一种自适应滑模控制算法,通过计算机仿真实验,验证了所提算法的有效性。
1 Norrbin非线性数学模型
在自动舵的设计中,本文选取Norrbin非线性数学模型来描述船舶操纵非线性运动[9]。

为了便于想控制器的设计,选取状态变量x1=Ψ,x2=r, u=(K/T)δ,则船舶运动的非线性模型为

从系统式(2)可以看出,本文的控制目标为设计控制器u,使系统输出y渐近跟踪航向期望值ψd,即当t→∞时,跟踪误差e=y-ψd→0。
2 基于 Backstepping的船舶航向自适应滑模控制器设计
对Norrbin船舶非线性系统(2),其舵角控制器的设计过程由二步组成。
Step 1 设船舶沿设定的航向dψ航行,定义航向误差

对(3)式求导,并考虑到系统(2)可得

将x2看作虚拟控制,取虚拟镇定函数

其中,c1为设计常数。定义函数

则式(4)可变为

定义Lyapunov函数

对其求导,可得
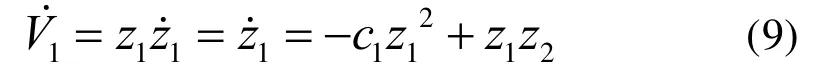
Step 2 定义滑模面函数

对其求导,并考虑式(6)、(7)可得

设计控制器u及参数自适应律为

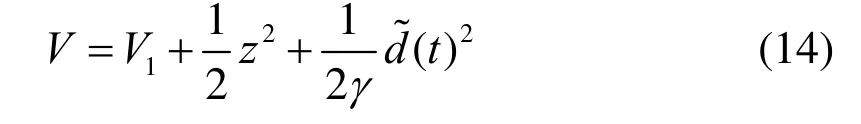
对其求导,并考虑式(9)、(11)和式(12)可得
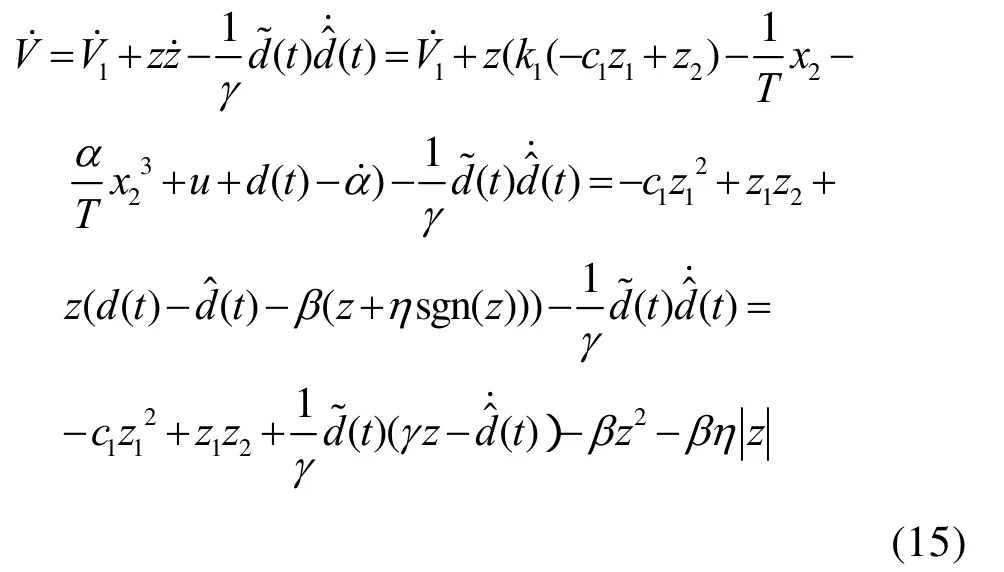
将式(13)代入式(15),可得

取

由于
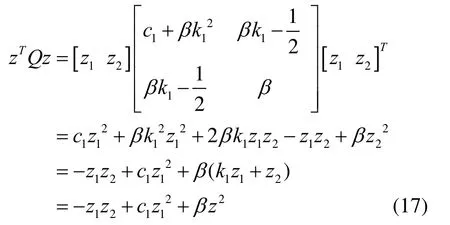
因此,式(16)可以变为

又由于

若适当选取β, c1和 k1,使得 β (c1+βk1)2>1/4,则有,从而可以保证Q为正定矩阵,因此(18)可变为0V≤˙。根据Lyapunov稳定性理论可知控制系统是渐近的。
3 仿真研究
针对某型船进行仿真研究,其参数如下[10]:T = 2 00,K = 0 .6,α = 3 0。应用Matlab/Simulink环境设计了系统(2)的自适应滑模控制算法程序,则参数设计为:c1=0.01, k1=0.35, β=1, y=0.01。假设期望航向值ψd=10°,将外界扰动d( t)等效为d( t)= 0 .01 + 0 .01sin(π t),与传统的PID控制相比较,仿真结果如图1和图2所示。
从图1可以看出,传统的PID控制虽然也可以跟踪航向角,但具有10%的超调量,这在实际控制中是不允许的。而新设计的控制器具有较快的响应速度和较好的跟踪能力,则能达到满意的效果。在图2中,传统的PID控制舵角抖振严重,而自适应滑模控制舵角光滑,舵角合理。总之,新设计的控制器具有较好的控制效果。

图1 航向角的变化曲线

图2 舵角的变化曲线
4 结束语
本文在考虑外界扰动的情况下,针对Norrbin非线性数学模型,采用Backstepping算法的设计方法,利用滑模控制强鲁棒性的特点,将自适应控制与滑模控制相结合,提出了一种新的自适应滑模控制算法,通过理论研究与仿真实验,与传统PID控制算法相比,具有较好的控制性能。
[1]Du J L, Guo C.Nonlinear adaptive design of course-tracking control of ship without a priori knowledge of control gain [J].Control Theory &Applications, 2005, 22(2): 315- 320.
[2]林永屹, 杜佳璐, 牛杰.基于 Backstepping的船舶航向自适应鲁棒非线性控制器设计[J].船舶工程, 2007, 29(1): 24-27.
[3]RAHMAN S U.Theory of constraints: a new review of the philosophy and its applications [J].International Journal of Operations and Production Management (S0144-3577), 1998, 18(4): 336-355.
[4]袁雷, 吴汉松.船舶航向非线性系统的多滑模自适应模糊控制[J].智能系统学报, 2010, 5(4):361-364.
[5]CHEE P T, CHRISTOPHER E.Sliding mode observers for reconstruction of simultaneous actuator and sensor faults[C]//Proceedings of the 42nd IEEE Conference on Decision and Control Maui Hawaii USA, 2003: 1455-1460.
[6]刘金琨.滑模变结构控制MATLAB仿真[M].北京: 清华大学出版社, 2005: 4-15.
[7]LIN F J, SHEN P H, HSU S P.Adaptive backstepping sliding mode control for linear induction motor drive[J].IEEE Proceeding Electrical Power Application, 2002, 149(3):184-194.
[8]LI K Y, JUN Z.Adaptive backstepping sliding mode design for TCSC[C]//The Sixth World Congress on Intelligent Control and Automation,2006: 1114-1117.
[9]张显库, 贾欣乐.船舶运动控制[M].北京: 国防工业出版社, 2005: 87-89.
[10]卜仁祥, 刘正江, 李铁山.迭代滑模增量反馈及在船舶航向控制中的应用[J].哈尔滨工程大学学报, 2007, 28(3): 268-272.
