考虑区域性的复杂电力网络演化模型
2012-07-02黄小庆曹丽华谭玉东
杨 蕾,黄小庆,曹丽华,谭玉东,刘 玙
(湖南大学电气与信息工程学院,长沙410082)
电力系统大停电事故频繁发生,后果日益严重,逐渐引起了人们对电网连锁故障传播机理和电力系统脆弱性的关注[1~14]。将复杂网络理论应用于对电力网络的脆弱性、鲁棒性以及连锁故障的研究成为一大热点课题[4~11]。把大电网中的发电厂和变电站等同于复杂网络中的节点,各输电线路等同于复杂网络中的连边,建立相应的大电网简化模型,是利用复杂网络理论研究大电网连锁故障的基础[8~10]。同时,电网本身的结构及演化规律具有内在、本质的特性,一旦确定下来,必然对电网的性能产生深刻的影响[6,7]。因此,研究电力网络的网络特性及其演化模型具有重要意义。
近年来,国内外学者提出了多种新的网络模型,并对这些模型所生成网络的特性进行了研究[2,3,15~16]。小世界模型和无标度模型的提出以及其特性的发现是复杂网络研究领域里最重要的研究成果[2,3]。小世界网络介于规则网络和随机网络之间,通过很小的概率切断规则网络中原始的边,并随机选择新的节点重新连接,它同时具有较大的聚类系数和较小的特征路径长度[2]。无标度网络的度分布在整体上服从幂律分布[3]。小世界特性使得电力网络中存在少量的节点拥有远远大于其他节点的介数,这些节点的缺失会导致大量最短路径的重新分布,进而引起系统连锁故障[9]。无标度网络源于其非同质的拓扑结构,对随机故障有惊人的鲁棒性,但对蓄意攻击则呈现出固有的脆弱性[14]。
当前经典的复杂网络模型与实际电力网络存在较大差异[21]。文献[15]证实了电力网络不是随机网络,也不是完全的无标度网络。文献[6]指出,部分电力网络不具有小世界特性,而部分电力网络的度分布不服从幂率分布也不服从指数分布。文献[22]提出了幂指数在1至3之间变化的网络模型,文献[23]提出了幂指数在1至3和2至3之间变化的网络模型,但文献[3]指出多数度分布为幂律分布的电力网络,其幂指数大于3。
本文从电力网络本身的演化机理入手,结合复杂网络领域最新的研究成果,提出一种改进的复杂电网邻域演化模型。通过理论分析给出了改进模型的度分布规律,通过对美国西部电网和中国华东电网的仿真以及与邻域演化网络、BA无标度网络、规则网络的对比,验证了该模型可以更好地拟合电力网络的演化。该模型的提出对于电力系统复杂性研究具有重要意义。
1 复杂网络模型及其特征参数
1.1 复杂网络模型简介
现实世界中的大多数复杂系统可以用网络的形式来描述。复杂网络模型研究即研究网络生成机制及演化模型。复杂网络的生成机制指的是网络的形成方式与形成过程,根据生成机制建立的模型称为复杂网络的演化模型。
针对现实网络中普遍存在的局域世界现象,文献[18]提出了局域世界演化模型,该模型在选取局域世界时使用了随机策略。而文献[20]建立的邻域演化模型,虽是随机选择邻域中心点,但以深度定义“邻域”,将局域世界的概念更加具体化。本文提出的模型在邻域演化模型的基础上考虑节点间距离的影响,重新定义“邻域”以及新节点接入网络的优选方式。基本的邻域演化模型的“邻域”定义为:假定在一个无权无向网络G中,标号为i和j的两个节点之间的距离dij定义为连接这两个节点的最短路径上的边数,即从节点i到节点j所需要经过的最少的边数。节点i的深度为p的邻域记为Np(i),则
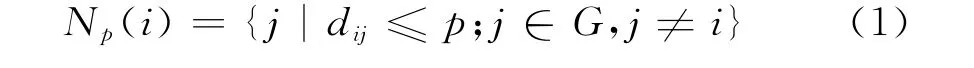
对于图1给出的网络,根据式1可得:N1(1)= {2,3},N2(1)= {2,3,4,7},图1(b)与图1(c)分别是节点1的深度为1、2的邻域示意图。
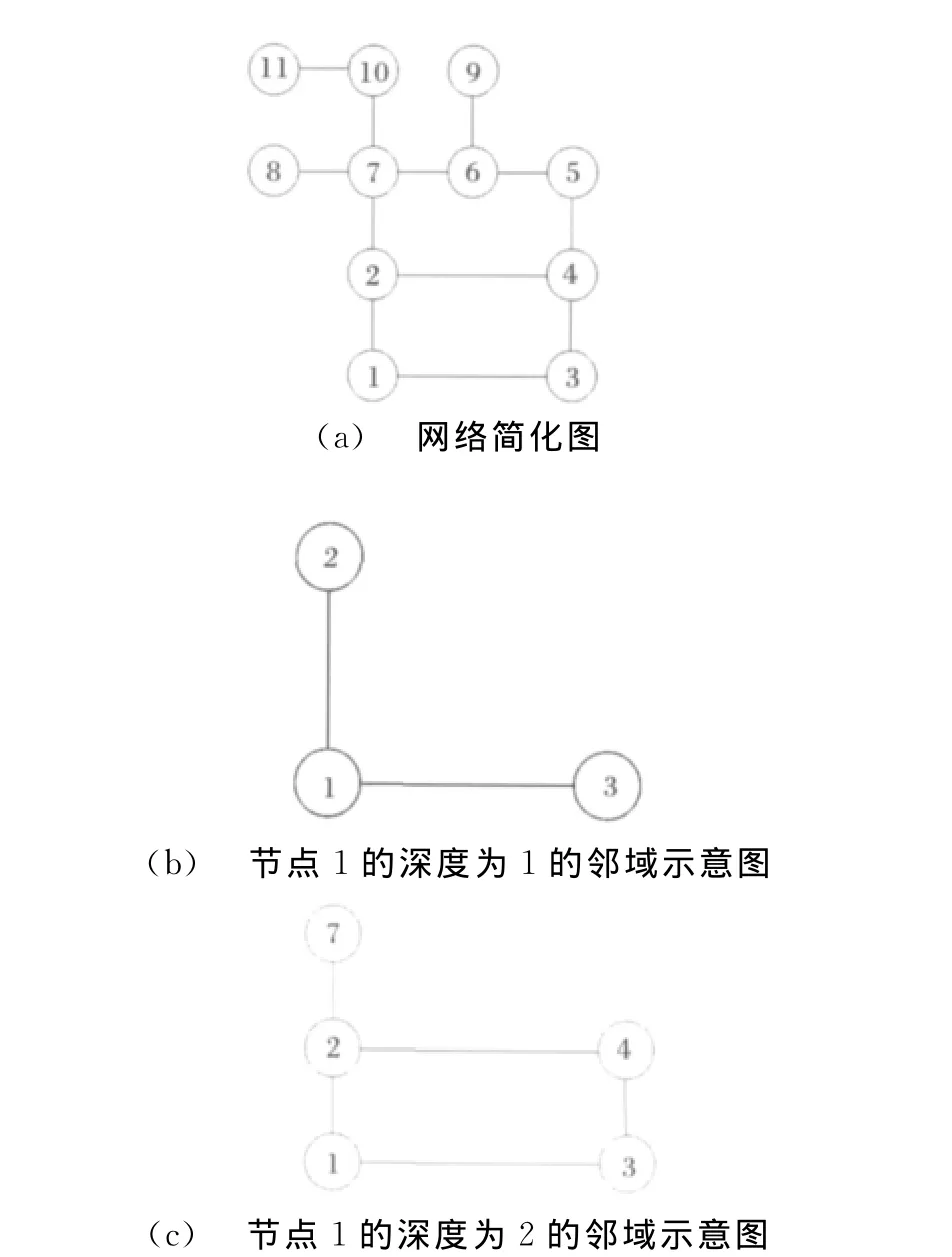
图1 “邻域”示意图Fig.1 Neighborhood schematic diagram
1.2 复杂网络的特征参数
从统计意义上讲,网络的拓扑特征参数包括度分布、特征路径长度、聚类系数等,其中最能反映网络拓扑特征的是度分布[7]。
节点i的度ki定义为与该节点连接的其他节点的数目。一个节点的度越大就意味着这个节点在某种意义上越“重要”。网络中所有节点i的度ki的平均值称为网络的平均度,记为<k>。度分布p(k)为网络中节点度数为k的概率。
2 改进的电力网络演化模型
2.1 电力网络拓扑建模原则和特征
电力网络可以抽象成为一个具有N个节点和E条线路的复杂网络,节点包括发电厂和变电站,而输电线、变压器支路是电网拓扑中的边。
随着社会经济的发展和电力需求的增加,不断有新的发电厂和变电站的投入,本模型使用节点和连接的增加模拟电网的生长。在电力网络的发展过程中,输电距离很大程度地影响了电网建设的经济成本。因此,新建发电厂和变电站一般从邻近的变电站输入电力,与以其位置为中心的一定地理范围内的周边变电站相连,电网的生长表现出一定的邻域演化特性。在优选连接方面,为达到一定的经济效益,新建厂站会与靠近自身的变电站相连,同时,为维持电力系统的稳定运行(N-1原则、暂态稳定等),新建厂站还需要与系统中承担“重要”输电作用的变电站相连,这些变电站往往具有较高的容量,与其他厂站的连接也较多。因此,电力网络的演化模型应该以一定的地理区域作为“邻域”范围,在新节点接入“邻域”时,定义概率q与距离近的节点相连,(1-q)与“邻域”内度数高的节点相连,达到经济与稳定运行的持平。
2.2 改进模型的构造算法
改进的网络演化模型按照如下算法构造。
1)增长:开始于较少的节点数(n0)和连接数(m0),每次新加入一个节点从网络中随机选择节点位置New_Pos,在二维空间中,New_Pos可用复数表示。
2)确定邻域世界:邻域世界的范围选取为New_Pos与网络中原有nI个节点Init_Pos之间距离的平均值,其表达式为
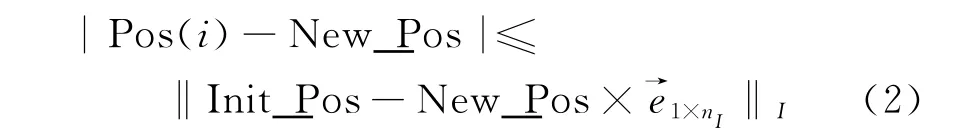
式中:Pos(i)为邻域内部节点的位置坐标;‖Init_Pos-New_Pos×‖I为原有节点坐标和新节点坐标向量差值的1-范数。图2给出N=200时的邻域示意图。
3)连接:新节点连接到m个已存在节点上,即产生m条连边,给定概率q,新加入的节点以q的概率与邻域中度数较高的节点相连,以(1-q)的概率与邻域中距离较近的节点相连。这样,邻域中节点i的优选因子∂i。
ki是节点i的度数,Di是节点i与新节点间的距离。经过t步,该模型产生一个具有N=t+n0个节点网络。
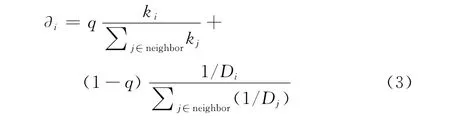
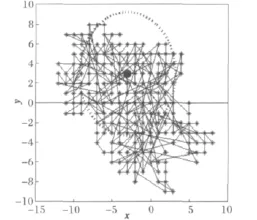
图2 新“邻域”示意图Fig.2 New Neighborhood schematic diagram
2.3 改进模型的度分布分析
使用平均场方法[24]分析电力网络改进演化模型的度分布规律。新节点连接到节点i的概率Π(ki)为
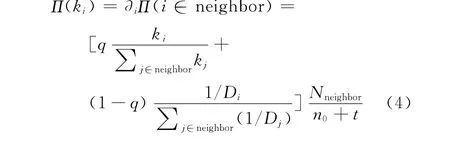
式中,Nneighbor为邻域内部的节点数。

利用微元法,当t很大时,均匀分布相邻节点间的距离d为

由式(6)得出:

近似求得:
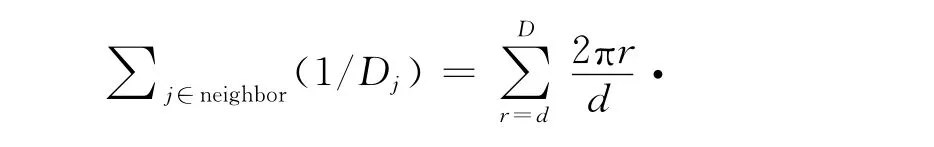
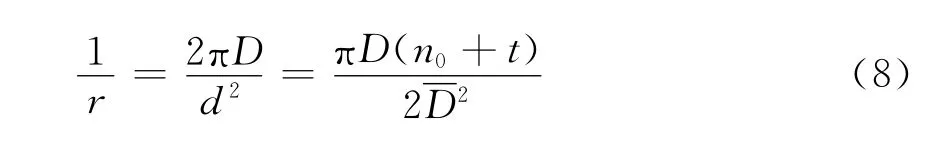
进一步,使用平均度数假设式(9)成立
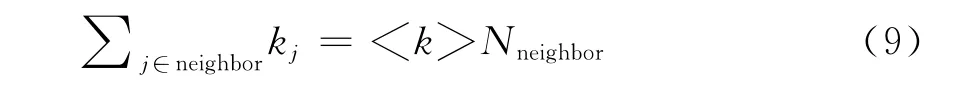
结合式(4)、(8)、(9)可得新节点连接到节点i的概率为
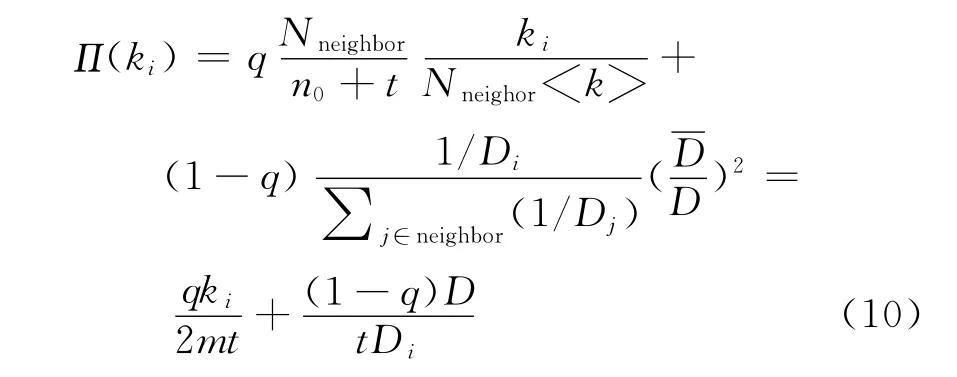
假设k是连续的,则概率Π(ki)可以看作ki的连续变化率,于是对于节点i有式(11):
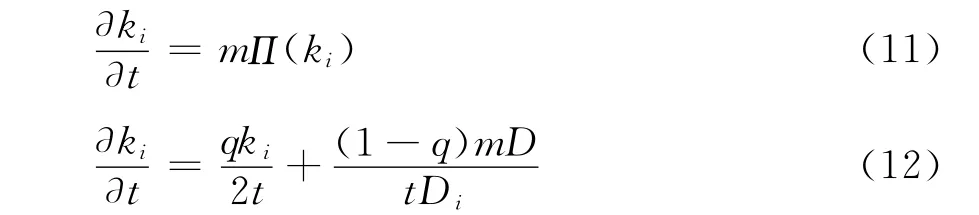
1)q≠0
采用文献[15]的计算方法,可得到度分布p(k)的表达式为

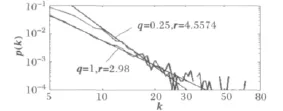
图3 改进模型的度幂律分布Fig.3 Power-law degree distribution of the new model
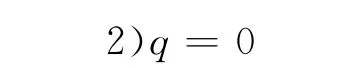
此时,式(12)变为
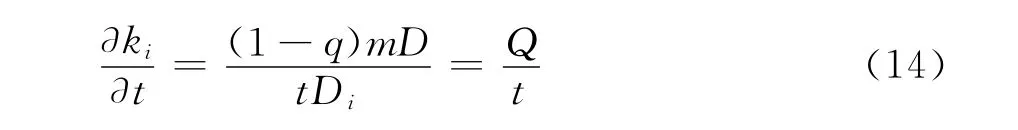
同理可得p(k)的表达式为
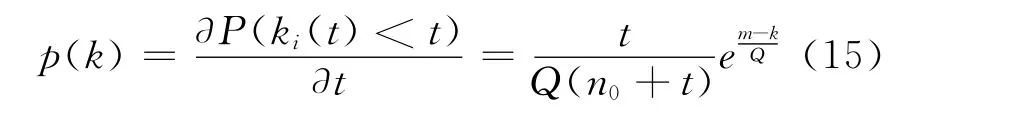
由式(15)可知,此时的度分布为指数分布。图4给出了N=5000,m=2时改进模型的度分布。
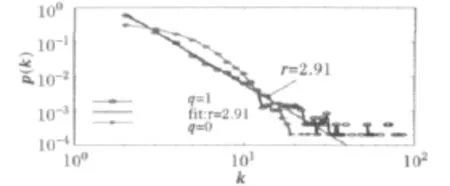
图4 改进模型的度指数分布Fig.4 Exponential degree distribution of the improved model
3 实例验证
下面给出中美两大电网的仿真结果以及与几种典型网络模型的对比数据。美国西部电网拥有4941个节点和6594条边。中国华东电网主要由上海、江苏、浙江、安徽、福建几省的电网组成,拥有769个节点,1029条边。改进模型仿真参数为m=2,仿真结果采用100次运行的平均值。
图5给出了美国西部电网与不同模型的度分布比较。由图5(a)可见,美国西部电网的度分布曲线接近于幂律分布,最佳幂律拟合函数为:p(k)=19×k-3.6,相关系数为0.9234,幂律指数r=3.6,介于3~∞。
当q=0,新节点接入电网时,只考虑输电距离影响,与靠近自身的节点相连(规则网络)[21];当q=1,新节点接入电网时,只考虑系统稳定性因素,与网络中度数高的节点相连(邻域演化网络)[20];图5(b)、(c)表明,二者生成的网络都不能很好地拟合美国西部电网的度分布,说明美国西部电网并非单纯的规则网络或邻域演化网络,两种演化方式都不能很好反映电力网络的演化规律。从图5(a)可看出,当q=0.8时,改进模型的度分布曲线与美国西部电网的实际度分布曲线最相符,证明了改进模型的有效性。同时,这表明电力网络的演化发展具有自身的特征,新节点接入原系统的方式与度、距离都有关,即新建厂站接入电力网络需要综合考虑输电距离以及系统的稳定性,改进模型能够很好地反映电力网络的演化规律。结合图5(a)、(d)可知,改进模型比BA无标度网络更接近实际网络。BA无标度网络1取参数m=2;BA无标度网络2取m=1。
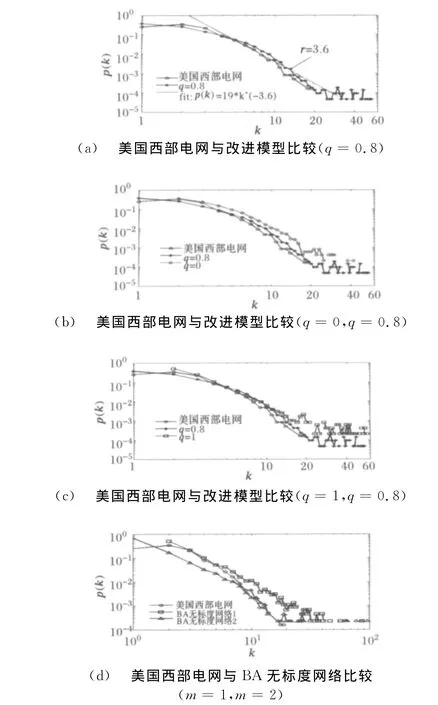
图5 美国西部电网与不同模型的度分布比较Fig.5 Degree distribution comparisons between West American power grid and different network models
由图6(a)可见,中国华东电网的最佳幂律拟合函数为:p(k)=87×k-4.2,相关系数为0.9017,幂律指数r=4.2,同样介于3~∞之间。仿真结果表明,当q=0.7时,改进模型可以很好地拟合中国华东电网的度分布曲线,华东电网的无标度性小于美国西部电网(q=0.8),在新节点接入电网时,美国西部电网以更高的概率与系统中节点度数高的节点相连,“富者更富”,网络节点的度数差异大,网络呈现出更强的非同质性,当发生随机故障时,无标度性强的电网通过小规模的线路连锁开断,释放系统压力,能够减少大停电概率;对于蓄意攻击,一旦无标度性强的电网中度数高的节点受损,则很可能导致大面积的停电。因此,中国华东电网承受随机故障的能力较弱,小规模的停电事故较多,但抵御蓄意故障的能力强,大规模事故的可能性少。图6(b)、(c)同样说明了华东电网并非单纯的规则网络(q=0)或邻域演化网络(q=1)。图6(a)、(d)表明改进模型比BA无标度网络(m=2)更好地反映中国华东电网的演化规律。
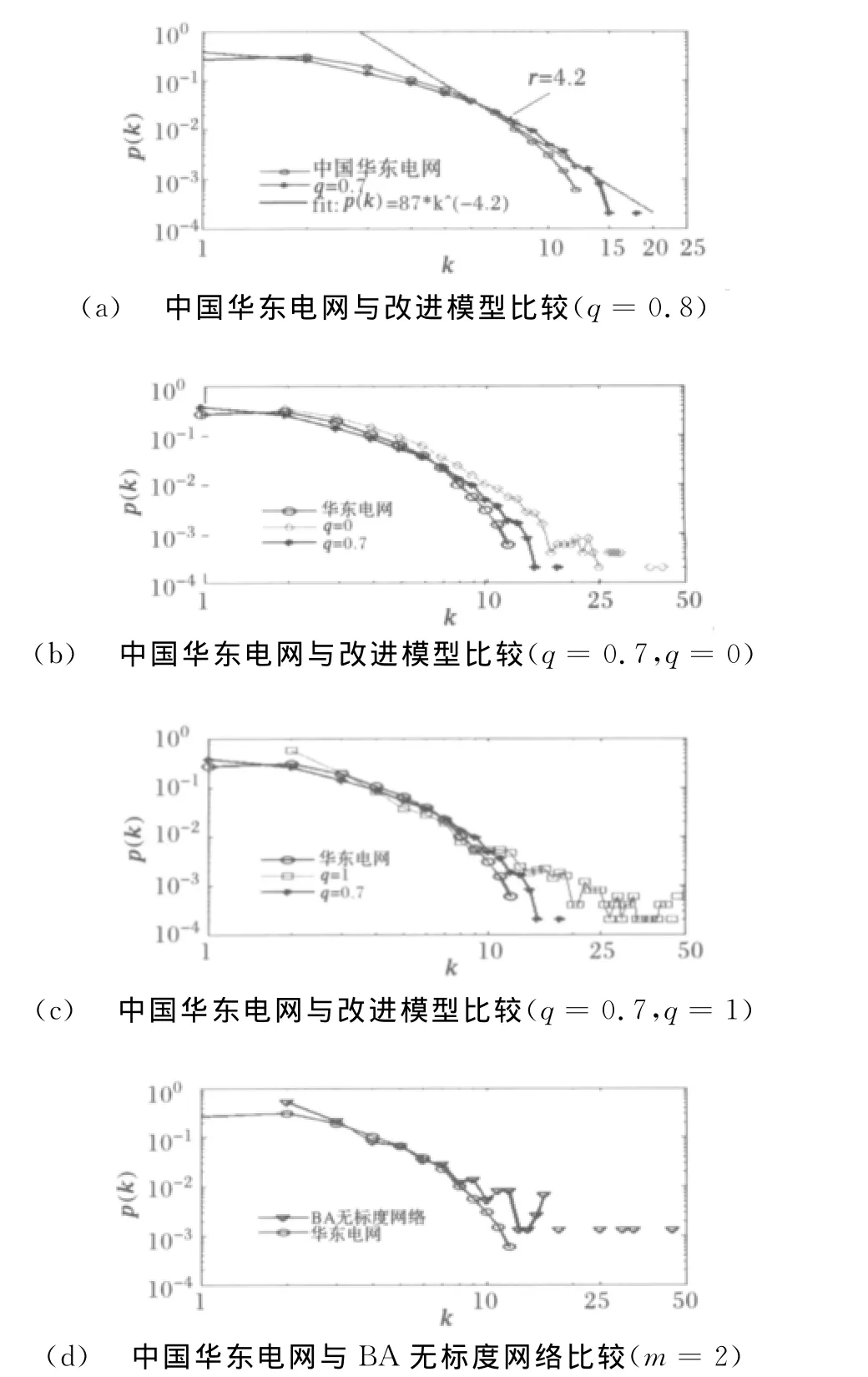
图6 中国华东电网不同模型的度分布比较Fig.6 Degree distribution comparisons between East China power grid and different network models
4 结语
本文在邻域演化模型的基础上,结合电力网络本身的发展机理,提出并研究了一种改进的电力网络演化模型,利用平均场理论分析了该模型演化为大电网时的度分布,并以中国华东电网和美国西部电网的仿真为例,说明了改进模型的度分布与实际电网的度分布更相符。进一步,通过把该模型与邻域演化网络、规则网络、BA无标度网络的对比,验证了实际电网既不是邻域演化网络,也不是完全的规则网络,而改进模型更能反映电力网络的演化规律。同时,仿真结果表明,中国华东电网的无标度性(q=0.7)低于美国西部电网(q=0.8),这意味着中国电网耐受蓄意袭击的能力强,大规模事故发生的可能性小,但抵御小规模事故的能力弱于美国电网。该模型的提出对于进一步复杂电网的动态特性研究具有重要意义。
[1] 曹一家,刘美君,丁理杰,等(Cao Yijia,Liu Meijun,Ding Lijie,et al).大电网安全性评估的系统复杂性理论研究(Research on system complexity theory for security evaluation of large power grids)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2007,19(1):1-8.
[2] Watts Duncan J,Strogatz Steven H.Collective dynamics of'small world'networks[J].Nature,1998,393(6684):440-442.
[3] Albert Laszlo Barabasi,Reka Albert.Emergence of scaling in random networks[J].Science,1999,286(5439):509-512.
[4] 夏德明,梅生伟,侯云鹤(Xia Deming,Mei Shengwei,Hou Yunhe).基于OTS的停电模型及其自组织临界性分析(A power system blackout model based on OTS and its self-organized criticality)[J].电力系统自动化(Automation of Electric Power Systems),2007,31(12):12-18,91.
[5] Bao Z J,Cao Y J,Wang G Z,et al.Analysis of cascading failure in electric grid based on power flow entropy[J].Physica Letters A,2009,373(34):3032-3040.
[6] 盂仲伟,鲁宗相,宋靖雁(Meng Zhongwei,Lu Zongxiang,Song Jingyan).中美电网的小世界拓扑模型比较分 析 (Comparison analysis of the small-world topological model of Chinese and American power grids)[J].电力系统自动化(Automation of Electric Power Systems),2004,28(15):21-24.
[7] 丁明,韩平平(Ding Ming,Han Pingping).基于小世界拓扑模型的大型电网脆弱性评估算法(Smallworld topological model based vulnerability assessment algorithm for large-scale power grid)[J].电力系统自动化(Automation of Electric Power Systems),2006,30(8):7-10,40.
[8] 梅生伟,翁晓峰,薛安成,等(Mei Shengwei,Weng Xiaofeng,Xue Ancheng,et al).基于最优潮流的停电模型及自组织临界性分析(Blackout model based on OPF and its self-organized criticality)[J].电力系统自动化(Automation of Electric Power Systems),2006,30(13):1-5,32.
[9] 丁理杰,曹一家,刘美君(Ding Lijie,Cao Yijia,Liu Meijun).复杂电力网络的连锁故障动态模型与分析(Dynamic modeling and analysis on cascading failure of complex power grids)[J].浙江大学学报:工学版(Journal of Zhejiang University:Engineering Science),2008,42(4):641-646.
[10]曹一家,陈晓刚,孙可(Cao Yijia,Chen Xiaogang,Sun Ke).基于复杂网络理论的大型电力系统脆弱线路辨识(Identification of vulnerable lines in power grid based on complex network theory)[J].电力自动化设备(Electric Power Automation Equipment),2006,26(12):1-5.
[11] 张国华,张建华,杨京燕,等(Zhang Guohua,Zhang Jianhua,Yang Jingyan,et al).基于有向权重图和复杂网络理论的大型电力系统脆弱性评估(Vulnerability assessment of bulk power grid based on weighted directional graph and complex network theory)[J].电力自动化设备(Electric Power Automation Equipment),2009,29(4):21-26.
[12]曹一家,丁理杰,王光增,等(Cao Yijia,Ding Lijie,Wang Guangzeng,et al).考虑网络演化的直流潮流停电模型与自组织临界性分析(Analysis on cascading failure and self-organized criticality in evolving power grids)[J].电力系统自动化(Automation of E-lectric Power Systems),2009,33(5):1-6.
[13] Albert Reka,Albert Istvan,Nakarado Gray L.Structural vulnerability of the North American power grid[J].Physical Review E,2004,69(2):1-4.
[14]易俊,周孝信,肖逾男(Yi Jun,Zhou Xiaoxin,Xiao Yunan).用连锁故障搜索算法判别系统的自组织临界 状 态 (Determining the self-organized criticality state of power systems by the cascading failures searching method)[J].中国电机工程学报(Proceedings of the CSEE),2007,27(25):1-5.
[15] 王光增,曹一家,包哲静,等(Wang Guangzeng,Cao Yijia,Bao Zhejing,et al).一种新型电力网络局域世界演化模型(A novel local-world evolving network model for power grid)[J].物理学报(Acta Physica Sinica),2009,58(6):3597-3602.
[16] 张培培,何阅,周涛,等(Zhang Peipei,He Yue,Zhou Tao,et al).一个描述合作网络顶点度分布的模型(A model describing the degree distribution of collab-oration networks)[J].物理学报(Acta Physica Sinica),2006,55(1):60-67.
[17] 史进,涂光瑜,罗毅(Si Jin,Tu Guangyu,Luo Yi).电力系统复杂网络特性分析与模型改进(Complex network characteristic analysis and model improving of the power system)[J].中国电机工程学报(Proceedings of the CSEE),2008,28(25):93-98.
[18]Li Xiang,Chen Guangrong.A local-world evolving network model[J].Physica A,2003,328(1-2):274-286.
[19]Yook S H,Jeong H,Barabasi A L,et al.Weighted evolving networks[J].Physical Review Letters,2001,86(25):5835-5838.
[20]Cao Y J,Wang G Z,Jiang Q Y,et al.A neighborhood evolving network model[J].Physics Letters A,2006,349(6):462-466.
[21] 王光增,曹一家,包哲静,等(Wang Guangzeng,Cao Yijia,Bao Zhejing,et al).一种复杂电力网络的时空演化模型(Temporal and spatial evolvement model of power grid)[J].电力自动化设备(Electric Power Automation Equipment),2009,29(1):1-5.
[22] 郭进利,汪丽娜(Guo Jinli,Wang Lina).幂律指数在1与3之间的一类无标度网络(Scale-free networks with the power-law exponent between 1and 3)[J].物理学报,2007,56(10):5635-5639.
[23]李季,汪秉宏,蒋品群,等(Li Ji,Wang Binghong,Jiang Pinqun,et al).节点数加速增长的复杂网络生长模型(Growing complex network model with acceleratingly increasing number of nodes)[J].物理学报(Acta Physica Sinica),2006,55(8):4051-4057.
[24] Albert Laszlo Barabasi, Albert Reka,Jeong Hawoong.Mean-field theory for scale-free random networks[J].Physica A,1999,272(1):173-187.
